codeforces 450B B. Jzzhu and Sequences(矩阵快速幂)

题目链接：

B. Jzzhu and Sequences

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Jzzhu has invented a kind of sequences, they meet the following property:

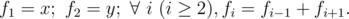
You are given x and y, please calculate fn modulo 1000000007 (109 + 7).

Input

The first line contains two integers x and y (|x|, |y| ≤ 109). The second line contains a single integer n (1 ≤ n ≤ 2·109).

Output

Output a single integer representing fn modulo 1000000007 (109 + 7).

Examples

 

input

2 3
3

output

1

input

0 -1
2

output

1000000006

Note

In the first sample, f2 = f1 + f3, 3 = 2 + f3, f3 = 1.

In the second sample, f2 =  - 1;  - 1 modulo (10^9 + 7) equals (10^9 + 6).

题意：

水题,不行说;

思路：

矩阵快速幂的水题;

AC代码：

#include <bits/stdc++.h>
using namespace std;
const int N=1e4+;
typedef long long ll;
const ll mod=1e9+;
ll n,x,y;
struct matrix
{
    ll a[][];
};
matrix mul(matrix A,matrix B)
{
    matrix s;
    s.a[][]=s.a[][]=;
    s.a[][]=s.a[][]=;
    for(int i=;i<;i++)
    {
        for(int j=;j<;j++)
        {
            s.a[i][j]=;
            for(int k=;k<;k++)
            {
                s.a[i][j]+=A.a[i][k]*B.a[k][j];
                s.a[i][j]%=mod;
            }
        }
    }
    return s;
}
ll fast_pow(matrix A,ll num)
{
    matrix s,base;
    for(int i=;i<;i++)
    {
        for(int j=;j<;j++)
        {
            s.a[i][j]=(i==j);
            base.a[i][j]=A.a[i][j];
        }
    }

    while(num)
    {
        if(num&)
        {
            s=mul(s,base);
        }
        base=mul(base,base);
        num=(num>>);
    }
    return (s.a[][]*y%mod+s.a[][]*x%mod)%mod;

}

int main()
{
    cin>>x>>y;
    cin>>n;
    matrix ma;
    ma.a[][]=ma.a[][]=;
    ma.a[][]=-;
    ma.a[][]=;
    if(n>)cout<<(fast_pow(ma,n-)%mod+mod)%mod<<"\n";
    else if(n==)cout<<(y%mod+mod)%mod<<"\n";
    else cout<<(x%mod+mod)%mod<<"\n";

}