Codeforces Round #393 (Div. 2)

A. Petr and a calendar

time limit per test：2 seconds

memory limit per test：256 megabytes

input：standard input

output：standard output

Petr wants to make a calendar for current month. For this purpose he draws a table in which columns correspond to weeks (a week is seven consequent days from Monday to Sunday), rows correspond to weekdays, and cells contain dates. For example, a calendar for January 2017 should look like on the picture:

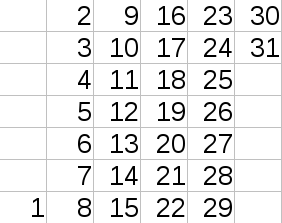
Petr wants to know how many columns his table should have given the month and the weekday of the first date of that month? Assume that the year is non-leap.

Input

The only line contain two integers m and d (1 ≤ m ≤ 12, 1 ≤ d ≤ 7) — the number of month (January is the first month, December is the twelfth) and the weekday of the first date of this month (1 is Monday, 7 is Sunday).

Output

Print single integer: the number of columns the table should have.

Examples

input

1 7

output

6

input

1 1

output

5

input

11 6

output

5

Note

The first example corresponds to the January 2017 shown on the picture in the statements.

In the second example 1-st January is Monday, so the whole month fits into 5 columns.

In the third example 1-st November is Saturday and 5 columns is enough.

题意：

假设没有闰年，给出每个月第一天是星期几，问这个月的日历有几列...

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
using namespace std;

int n,m,ans=0;

inline int judge(int x){
	if(x<=7){
		if(x&1)
			return 31;
		else if(x==2)
			return 28;
		else
			return 30;
	}
	else{
		if(x&1)
			return 30;
		return 31;
	}
}

signed main(void){
	scanf("%d%d",&n,&m);
	n=judge(n);
	n-=7-m+1;
	ans=1+(n+6)/7;
	printf("%d\n",ans);
	return 0;
}//Cap ou pas cap. Cap.

 

B. Frodo and pillows

time limit per test：1 second

memory limit per test：256 megabytes

input：standard input

output：standard output

n hobbits are planning to spend the night at Frodo's house. Frodo has n beds standing in a row and m pillows (n ≤ m). Each hobbit needs a bed and at least one pillow to sleep, however, everyone wants as many pillows as possible. Of course, it's not always possible to share pillows equally, but any hobbit gets hurt if he has at least two pillows less than some of his neighbors have.

Frodo will sleep on the k-th bed in the row. What is the maximum number of pillows he can have so that every hobbit has at least one pillow, every pillow is given to some hobbit and no one is hurt?

Input

The only line contain three integers n, m and k (1 ≤ n ≤ m ≤ 109, 1 ≤ k ≤ n) — the number of hobbits, the number of pillows and the number of Frodo's bed.

Output

Print single integer — the maximum number of pillows Frodo can have so that no one is hurt.

Examples

input

4 6 2

output

2

input

3 10 3

output

4

input

3 6 1

output

3

Note

In the first example Frodo can have at most two pillows. In this case, he can give two pillows to the hobbit on the first bed, and one pillow to each of the hobbits on the third and the fourth beds.

In the second example Frodo can take at most four pillows, giving three pillows to each of the others.

In the third example Frodo can take three pillows, giving two pillows to the hobbit in the middle and one pillow to the hobbit on the third bed.

题意：

有n张床排成一行，Frodo在第k张床，共有m个枕头，每个人至少有1个枕头，并且每个人相邻的两个人只能比他多至多一个枕头，问Frodo最多可以得到多少个枕头...

分析：

二分答案...

最优解一定是阶梯型的...

假设Frodo的一边有y张床，当前二分的ans=x，如果y大于x-1，那么这一边加上Frodo最少共有$\frac{(x+1)x}{2}+y-(x-1)$个枕头，否则就是$\frac{(x+x-y)(y+1)}{2}$...然后判断就好了...

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
using namespace std;

int n,m,k;

inline long long calc(int x,int y){
	if(!y)
		return x;
	if(!x)
		return 0;
	if(y>x-1)
		return 1LL*(x+1)*x/2LL+y-(x-1);
	return 1LL*(x+x-y)*(y+1)/2LL;
}

signed main(void){
	scanf("%d%d%d",&n,&m,&k);
	int l=0,r=1e9,ans=0;
	while(l<=r){
		int mid=(l+r)>>1;
		if(calc(mid,k-1)+calc(mid,n-k)-mid<=m)
			ans=mid,l=mid+1;
		else
			r=mid-1;
	}
	printf("%d\n",ans);
	return 0;
}//Cap ou pas cap. Cap.

C. Pavel and barbecue

time limit per test：2 seconds

memory limit per test：256 megabytes

input：standard input

output：standard output

Pavel cooks barbecue. There are n skewers, they lay on a brazier in a row, each on one of n positions. Pavel wants each skewer to be cooked some time in every of n positions in two directions: in the one it was directed originally and in the reversed direction.

Pavel has a plan: a permutation p and a sequence b1, b2, ..., bn, consisting of zeros and ones. Each second Pavel move skewer on position i to position pi, and if bi equals 1 then he reverses it. So he hope that every skewer will visit every position in both directions.

Unfortunately, not every pair of permutation p and sequence b suits Pavel. What is the minimum total number of elements in the given permutation p and the given sequence b he needs to change so that every skewer will visit each of 2n placements? Note that after changing the permutation should remain a permutation as well.

There is no problem for Pavel, if some skewer visits some of the placements several times before he ends to cook. In other words, a permutation p and a sequence b suit him if there is an integer k (k ≥ 2n), so that after k seconds each skewer visits each of the 2nplacements.

It can be shown that some suitable pair of permutation p and sequence b exists for any n.

Input

The first line contain the integer n (1 ≤ n ≤ 2·105) — the number of skewers.

The second line contains a sequence of integers p1, p2, ..., pn (1 ≤ pi ≤ n) — the permutation, according to which Pavel wants to move the skewers.

The third line contains a sequence b1, b2, ..., bn consisting of zeros and ones, according to which Pavel wants to reverse the skewers.

Output

Print single integer — the minimum total number of elements in the given permutation p and the given sequence b he needs to change so that every skewer will visit each of 2n placements.

Examples

input

4
4 3 2 1
0 1 1 1

output

2

input

3
2 3 1
0 0 0

output

1

Note

In the first example Pavel can change the permutation to 4, 3, 1, 2.

In the second example Pavel can change any element of b to 1.

题意：

我真的没看懂题...现在都没看懂TAT...

D. Travel Card

time limit per test：2 seconds

memory limit per test：256 megabytes

input：standard input

output：standard output

A new innovative ticketing systems for public transport is introduced in Bytesburg. Now there is a single travel card for all transport. To make a trip a passenger scan his card and then he is charged according to the fare.

The fare is constructed in the following manner. There are three types of tickets:

1. a ticket for one trip costs 20 byteland rubles,
2. a ticket for 90 minutes costs 50 byteland rubles,
3. a ticket for one day (1440 minutes) costs 120 byteland rubles.

Note that a ticket for x minutes activated at time t can be used for trips started in time range from t to t + x - 1, inclusive. Assume that all trips take exactly one minute.

To simplify the choice for the passenger, the system automatically chooses the optimal tickets. After each trip starts, the system analyses all the previous trips and the current trip and chooses a set of tickets for these trips with a minimum total cost. Let the minimum total cost of tickets to cover all trips from the first to the current is a, and the total sum charged before is b. Then the system charges the passenger the sum a - b.

You have to write a program that, for given trips made by a passenger, calculates the sum the passenger is charged after each trip.

Input

The first line of input contains integer number n (1 ≤ n ≤ 105) — the number of trips made by passenger.

Each of the following n lines contains the time of trip ti (0 ≤ ti ≤ 109), measured in minutes from the time of starting the system. All ti are different, given in ascending order, i. e. ti + 1 > ti holds for all 1 ≤ i < n.

Output

Output n integers. For each trip, print the sum the passenger is charged after it.

Examples

input

3
10
20
30

output

20
20
10

input

10
13
45
46
60
103
115
126
150
256
516

output

20
20
10
0
20
0
0
20
20
10

Note

In the first example, the system works as follows: for the first and second trips it is cheaper to pay for two one-trip tickets, so each time 20 rubles is charged, after the third trip the system understands that it would be cheaper to buy a ticket for 90 minutes. This ticket costs 50 rubles, and the passenger had already paid 40 rubles, so it is necessary to charge 10 rubles only.

题意：

有三种车票可供选择：

No.0 坐一站，花费为20

No.1 坐90-1分钟，花费为50(因为在站台需要花费1分钟，所以要-1)

No.2 坐1440-1分钟，花费为120

给出n个站点，每一次给出到下一站点的时间，每一次买票都是最优选择，问每一次买票需要多交多少钱...

分析：

感觉这就是裸的DP然后输出每一次的结果减去上一次的结果...

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
using namespace std;

const int maxn=100000+5;

int n,t[maxn];

long long f[maxn];

signed main(void){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&t[i]);
	f[0]=0;
	for(int i=1;i<=n;i++){
		f[i]=f[i-1]+20;
		long long a=lower_bound(t+1,t+n+1,t[i]-89  )-t-1,w1=20*(i-a+1);
		long long b=lower_bound(t+1,t+n+1,t[i]-1439)-t-1,w2=20*(i-b+1);
		if(w1>50 )
			f[i]=min(f[i],f[a]+50 );
		else
			f[i]=min(f[i],f[a]+w1);
		if(w2>120)
			f[i]=min(f[i],f[b]+120);
		else
			f[i]=min(f[i],f[b]+w2);
		printf("%I64d\n",f[i]-f[i-1]);
	}
	return 0;
}//Cap ou pas cap. Cap.

 

E. Nikita and stack

time limit per test：2 seconds

memory limit per test：256 megabytes

input：standard input

output：standard output

Nikita has a stack. A stack in this problem is a data structure that supports two operations. Operation push(x) puts an integer x on the top of the stack, and operation pop() deletes the top integer from the stack, i. e. the last added. If the stack is empty, then the operation pop() does nothing.

Nikita made m operations with the stack but forgot them. Now Nikita wants to remember them. He remembers them one by one, on the i-th step he remembers an operation he made pi-th. In other words, he remembers the operations in order of some permutation p1, p2, ..., pm. After each step Nikita wants to know what is the integer on the top of the stack after performing the operations he have already remembered, in the corresponding order. Help him!

Input

The first line contains the integer m (1 ≤ m ≤ 105) — the number of operations Nikita made.

The next m lines contain the operations Nikita remembers. The i-th line starts with two integers pi and ti (1 ≤ pi ≤ m, ti = 0 or ti = 1) — the index of operation he remembers on the step i, and the type of the operation. ti equals 0, if the operation is pop(), and 1, is the operation is push(x). If the operation is push(x), the line also contains the integer xi (1 ≤ xi ≤ 106) — the integer added to the stack.

It is guaranteed that each integer from 1 to m is present exactly once among integers pi.

Output

Print m integers. The integer i should equal the number on the top of the stack after performing all the operations Nikita remembered on the steps from 1 to i. If the stack is empty after performing all these operations, print -1.

Examples

input

2
2 1 2
1 0

output

2
2

input

3
1 1 2
2 1 3
3 0

output

2
3
2

input

5
5 0
4 0
3 1 1
2 1 1
1 1 2

output

-1
-1
-1
-1
2

Note

In the first example, after Nikita remembers the operation on the first step, the operation push(2) is the only operation, so the answer is 2. After he remembers the operation pop() which was done before push(2), answer stays the same.

In the second example, the operations are push(2), push(3) and pop(). Nikita remembers them in the order they were performed.

In the third example Nikita remembers the operations in the reversed order.

题意：

有一个栈...(就是普通的栈...

有m个操作，但是这m个操作不是按顺序给出的...每一次给出第p[i]个操作，每一次都询问按顺序执行完前i个给出操作后的栈顶元素...

分析：

我们把出栈操作看作-1，入栈操作看作+1，那么倒着数第一个使得操作为+的元素就是栈顶元素...

所以问题就转化为了每次给一个位置+1或者-1，最靠右的使得后缀和为1的数是多少...

这不就是线段树么...

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
using namespace std;

const int maxn=100000+5;

int n,w[maxn];

struct Tree{
	int l,r,push,pop;
}tree[maxn<<2];

inline void build(int l,int r,int tr){
	tree[tr].l=l,tree[tr].r=r,tree[tr].push=tree[tr].pop=0;
	if(l==r)
		return;
	int mid=(l+r)>>1;
	build(l,mid,tr<<1);build(mid+1,r,tr<<1|1);
}

inline void change(int pos,int x,int tr){
	if(tree[tr].l==tree[tr].r){
		if(x)
			tree[tr].push=1;
		else
			tree[tr].pop=1;
		return;
	}
	int mid=(tree[tr].l+tree[tr].r)>>1;
	if(pos<=mid)
		change(pos,x,tr<<1);
	else
		change(pos,x,tr<<1|1);
	int lala=min(tree[tr<<1].push,tree[tr<<1|1].pop);
	tree[tr].push=tree[tr<<1].push+tree[tr<<1|1].push-lala;
	tree[tr].pop =tree[tr<<1].pop +tree[tr<<1|1].pop -lala;
}

inline int query(int sum,int tr){
	if(!tree[tr].push)
		return -1;
	if(tree[tr].l==tree[tr].r)
		return w[tree[tr].l];
	int mid=(tree[tr].l+tree[tr].r)>>1;
	if(tree[tr<<1|1].push+sum>0)
		return query(sum,tr<<1|1);
	else
		return query(sum+tree[tr<<1|1].push-tree[tr<<1|1].pop,tr<<1);
}

signed main(void){
	scanf("%d",&n);build(1,n,1);
	for(int i=1,pos,opt,x;i<=n;i++){
		scanf("%d%d",&pos,&opt);
		if(opt==1)
			scanf("%d",&w[pos]);
		change(pos,opt,1);
		printf("%d\n",query(0,1));
	}
	return 0;
}//Cap ou pas cap. Cap.

　　

　

---

By NeighThorn