Python-S9-Day128——算法基础Algorithm

• 01 算法基本概念与递归；

• 02 二分查找与LOW B三人组

• 03 快速排序

• 04 归并排序

01 算法基本概念与递归；

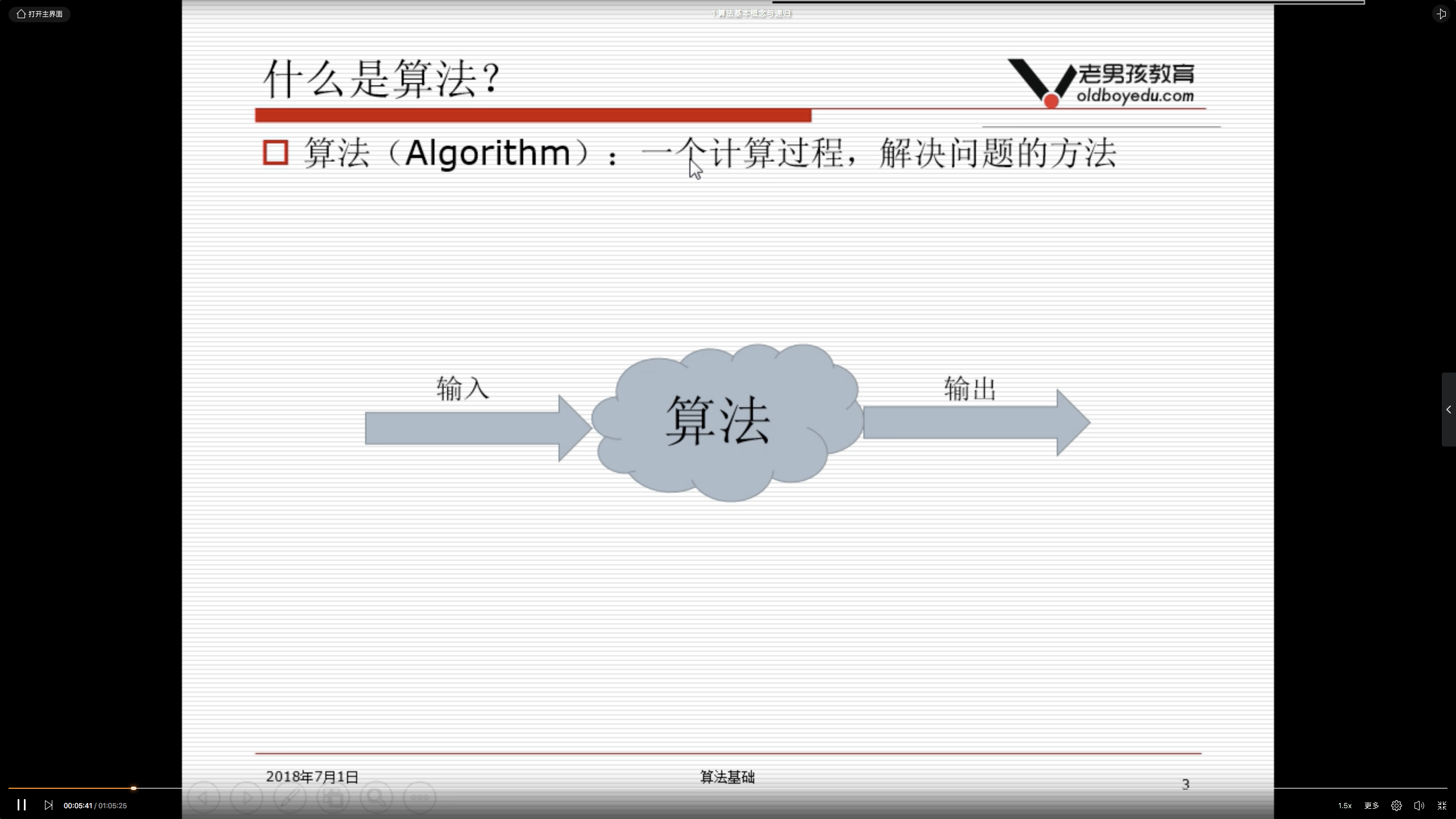
1.1 算法概念

1.2 复习：递归

1.3 时间复杂度

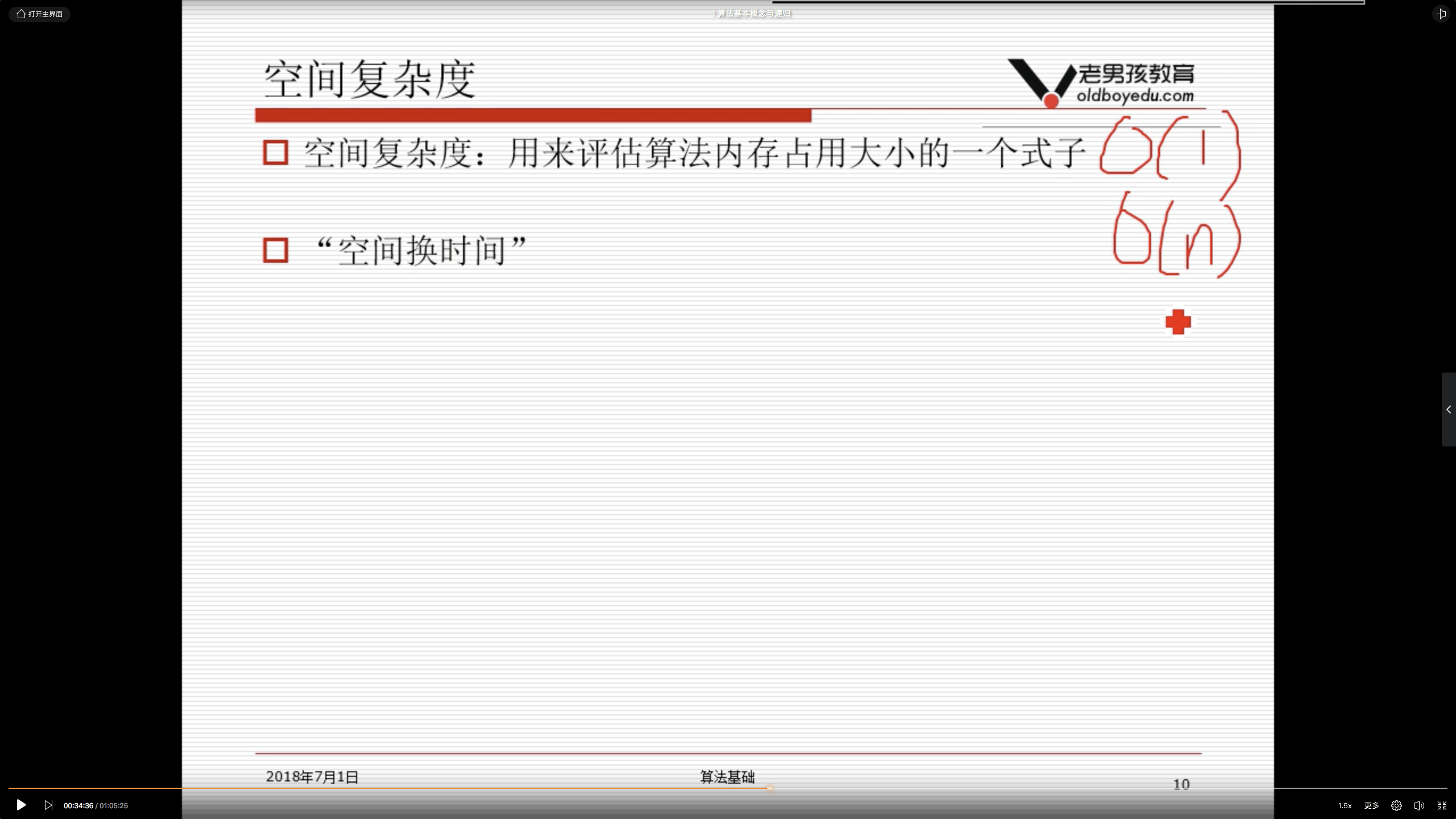
1.4 空间复杂度

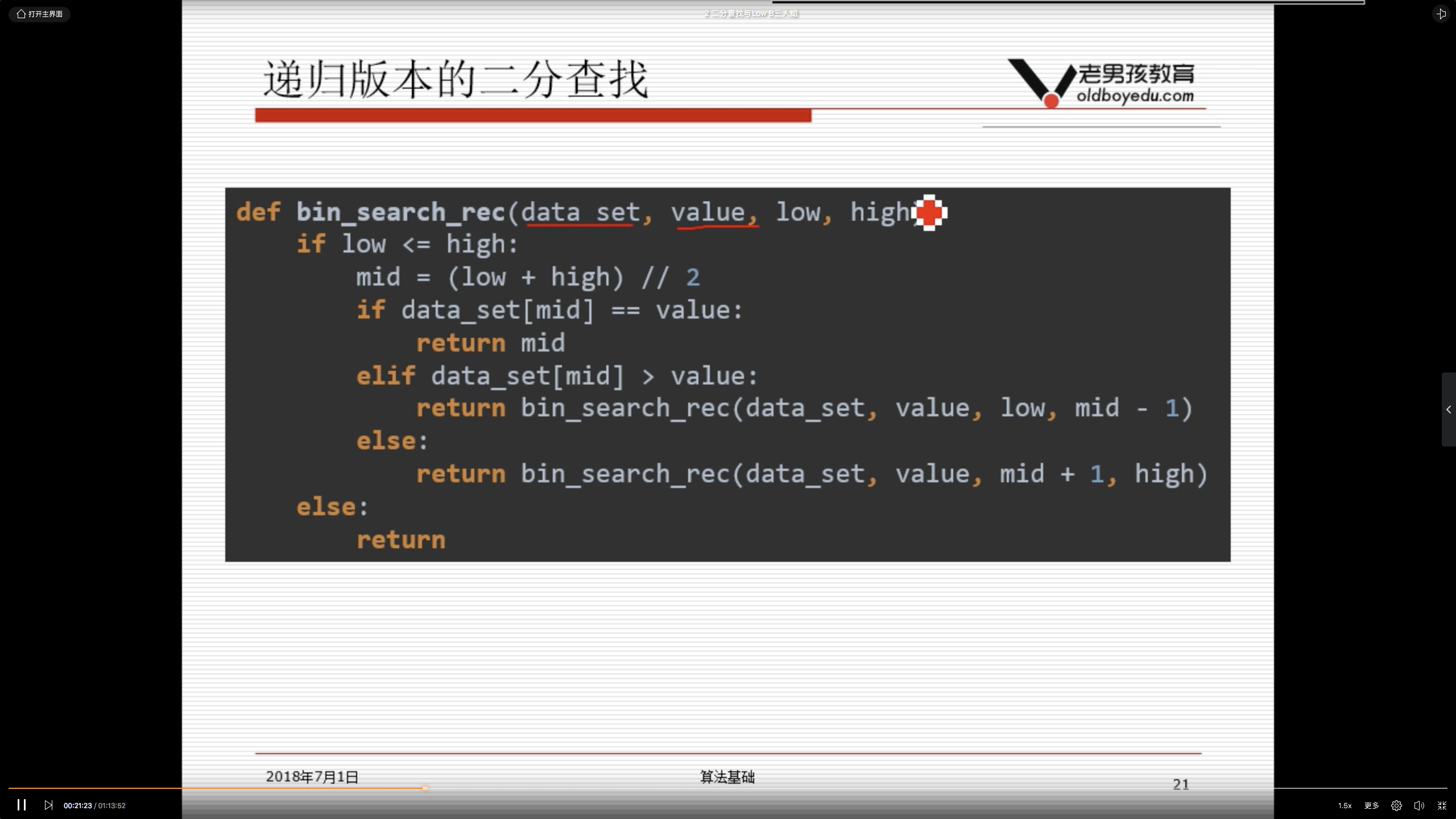
1.5 递归

def func3(n):
    if n > 0:
        func3(n - 1)
        print(n)

func3(5)

def text(n):
    if n > 0:
        print('抱着', end='')
        text(n - 1)
        print('的我', end='')
    else:
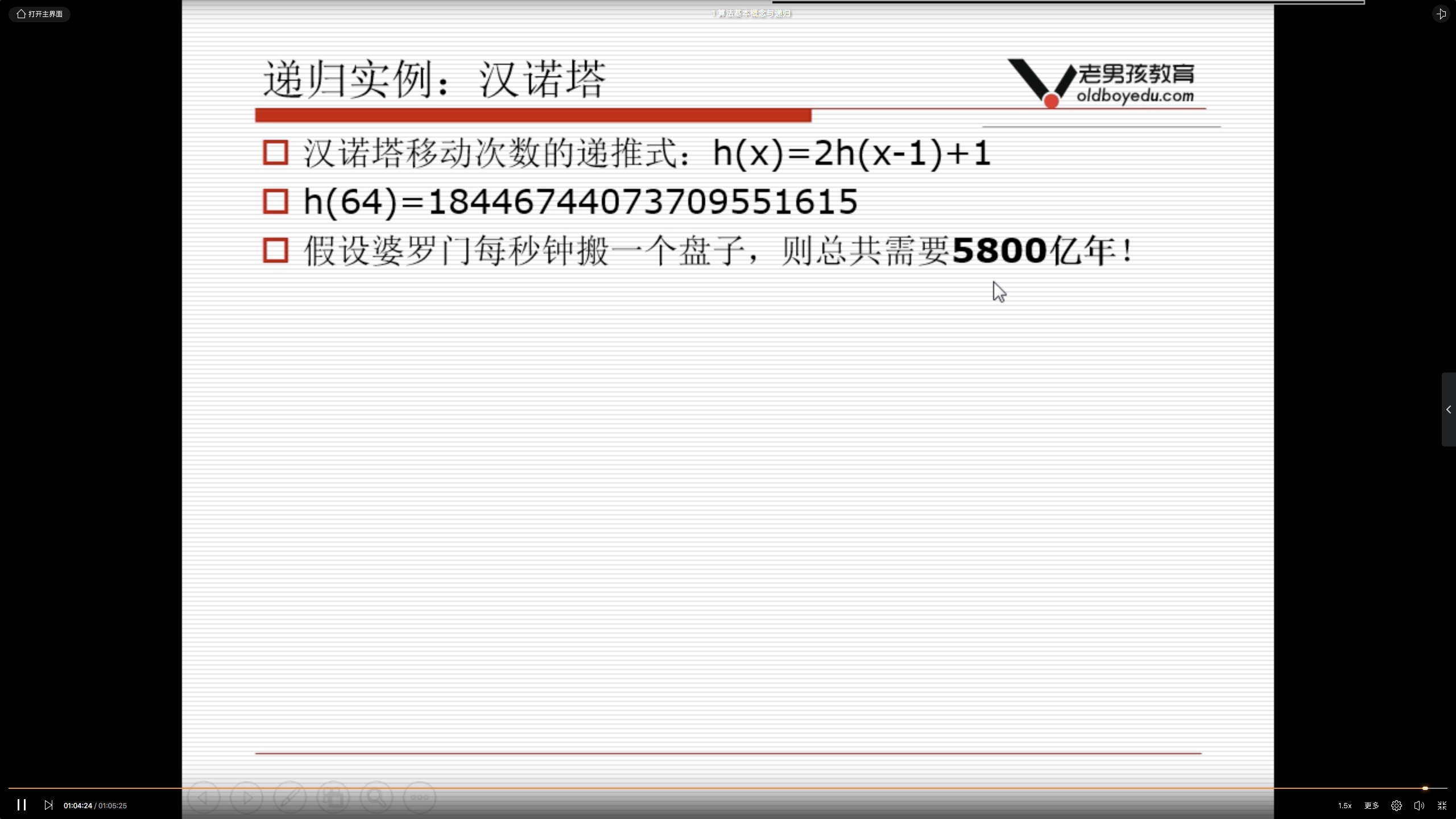
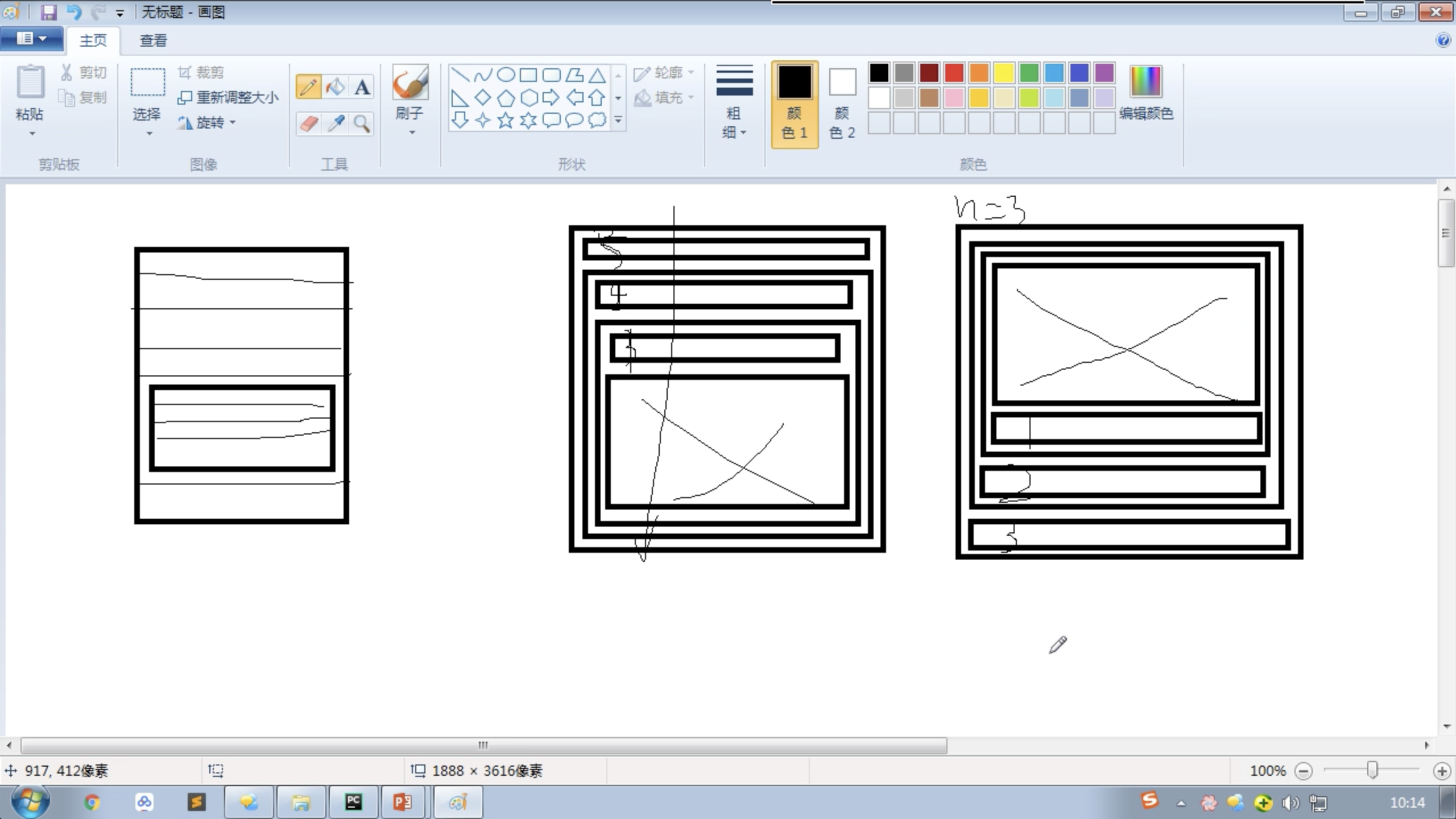
        print("我的小鲤鱼", end='')

text(5)

# 汉诺塔问题
def hanoi(n, A, B, C):
    if n >0:
        # n个盘子从A经过B移动到C；
        hanoi(n - 1, A, C, B)
        print("%s->%s" % (A, C))
        hanoi(n - 1, B, A, C)

hanoi(3, "A", "B", "C")

1.6 汉诺塔问题（递归的经典）

02 二分查找与LOW B三人组

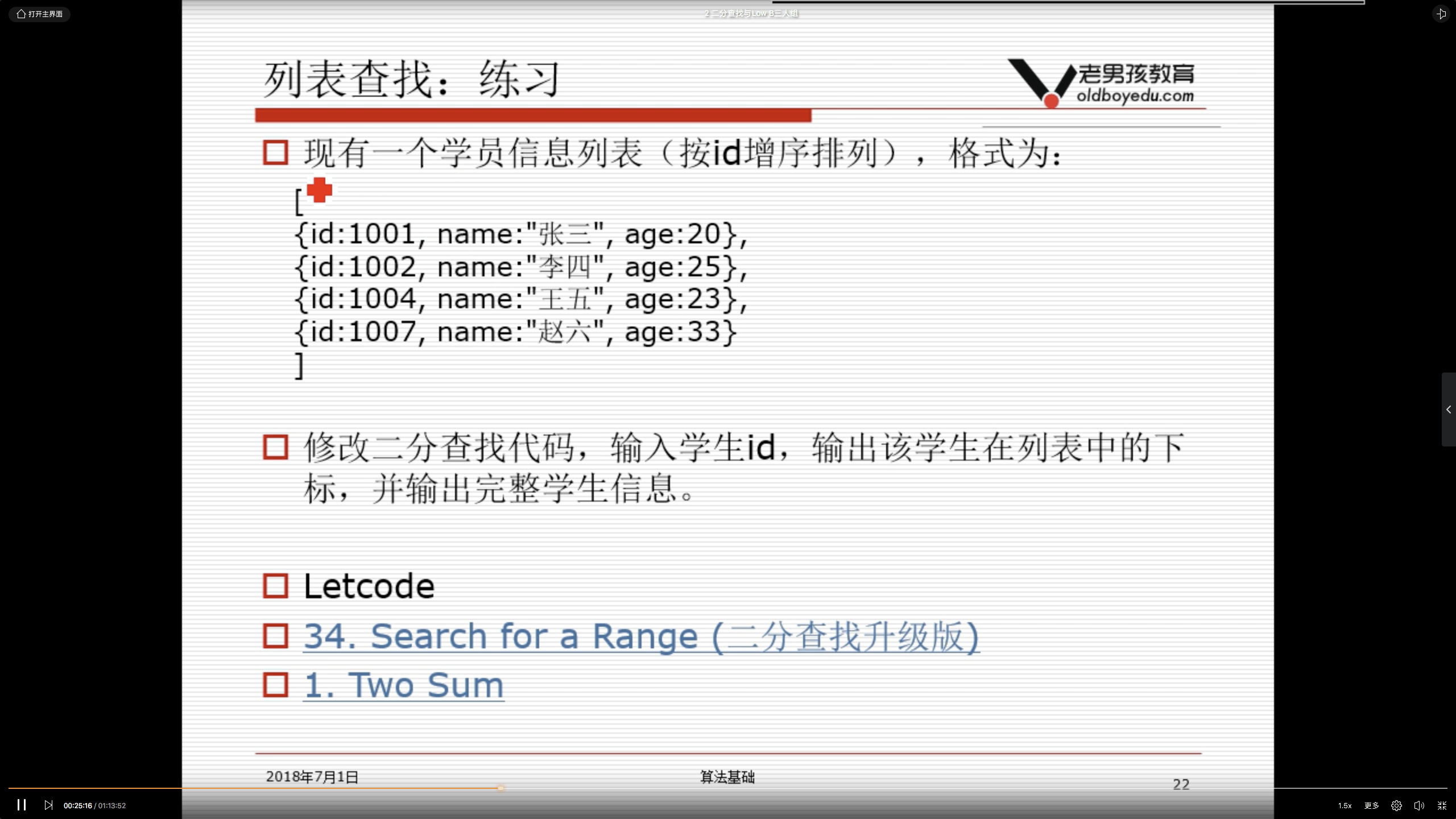
2.1 列表查找；

2.2  顺序查找；

2.3 二分查找（本身有序）；

import time

def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time:%s secs." % (func.__name__, t2 - t1))
        return result

    return wrapper

# 线性查找；
@cal_time
def binary_search(li, val):
    low = 0
    high = len(li) - 1

    while low <= high:
        mid = (low + high) // 2
        if li[mid] > val:
            high = mid - 1
        elif li[mid] < val:
            low = mid + 1
        else:
            return mid
    else:
        return None

# 二分查找；
@cal_time
def linear_search(li, val):
    try:
        i = li.index(val)
        return i
    except:
        return None

li = list(range(0, 100000000, 2))
times = binary_search(li, 9000006)
print(times)
times1 = linear_search(li, 9000006)
print(times1)

2.4 列表排序；

　　2.4.1 列表排序

• 将无序列表变成有序列表

　　2.4.2 应用场景

• 各种榜单
• 各种表格
• 给二分查找使用
• 给其他算法使用

　　2.4.3 输入：无序列表

　　2.4.4 输出：有序列表

　　2.4.5 升序与降序

　　2.4.6 排序LOW B 三人组

• 冒泡排序
• 选择排序
• 插入排序

　　2.4.7 排序NB三人组

• 快速排序
• 堆排序
• 归并排序

　　2.4.8 没什么人用的排序

• 基数排序
• 希尔排序
• 桶排序
• 计数排序

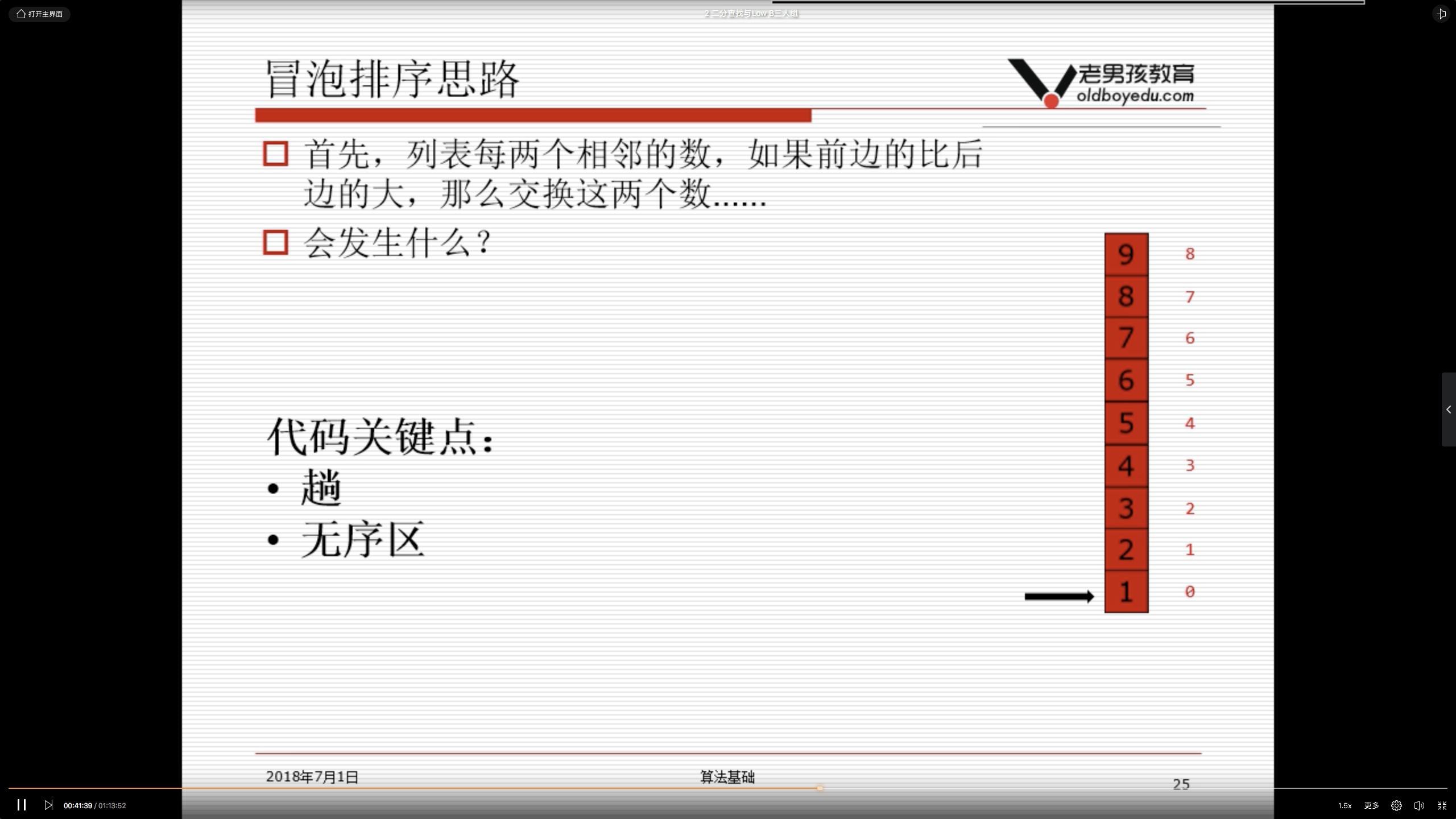
　　2.4.9 算法关键点

• 有序区域
• 无序区域

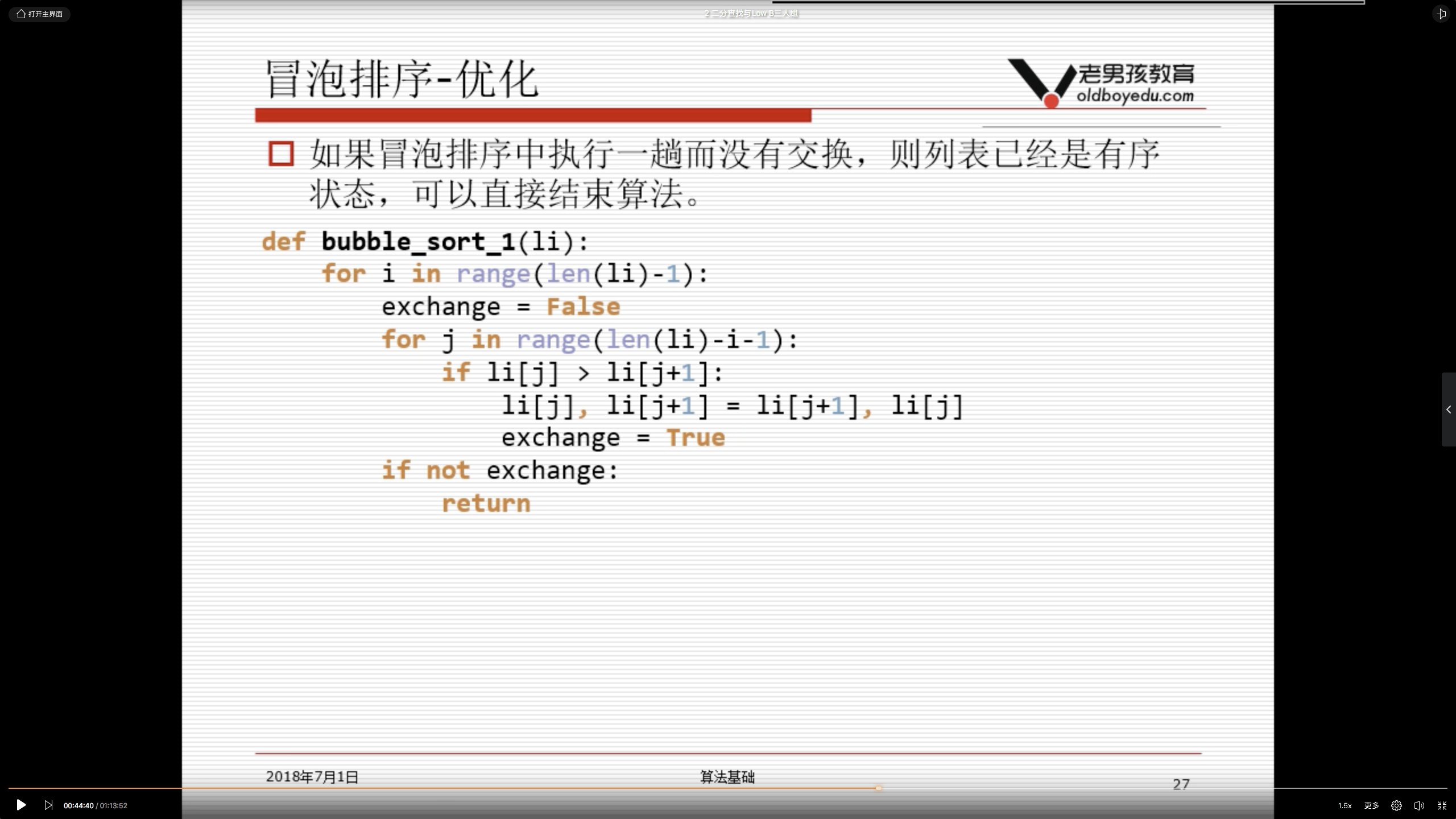
• 冒泡算法优化思路——如果冒泡排序中执行一趟而没有交换，则列表已经是有序的状态，可以直接结束算法；

buddle_sort.py;

from cal_time import cal_time

@cal_time
def buddle_sort(li):
    for i in range(0, len(li) - 1):
        # i 是表示第i趟，此时有序区有i个数；
        for j in range(0, len(li) - i - 1):
            if li[j] > li[j + 1]:
                li[j], li[j + 1] = li[j + 1], li[j]

import random

li = list(range(10000))
random.shuffle(li)
buddle_sort(li)
print(li)

二分查找优化算法：

buddle_sort_opt.py；

from cal_time import cal_time

@cal_time
def buddle_sort(li):
    for i in range(0, len(li) - 1):
        exchange = False
        # i 是表示第i趟，此时有序区有i个数；
        for j in range(0, len(li) - i - 1):
            if li[j] > li[j + 1]:
                li[j], li[j + 1] = li[j + 1], li[j]
                exchange = True
        if not exchange:
            return

import random

li = list(range(10000))
# random.shuffle(li)
buddle_sort(li)
print(li)

cal_time.py;

import time

def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time:%s secs." % (func.__name__, t2 - t1))
        return result

    return wrapper

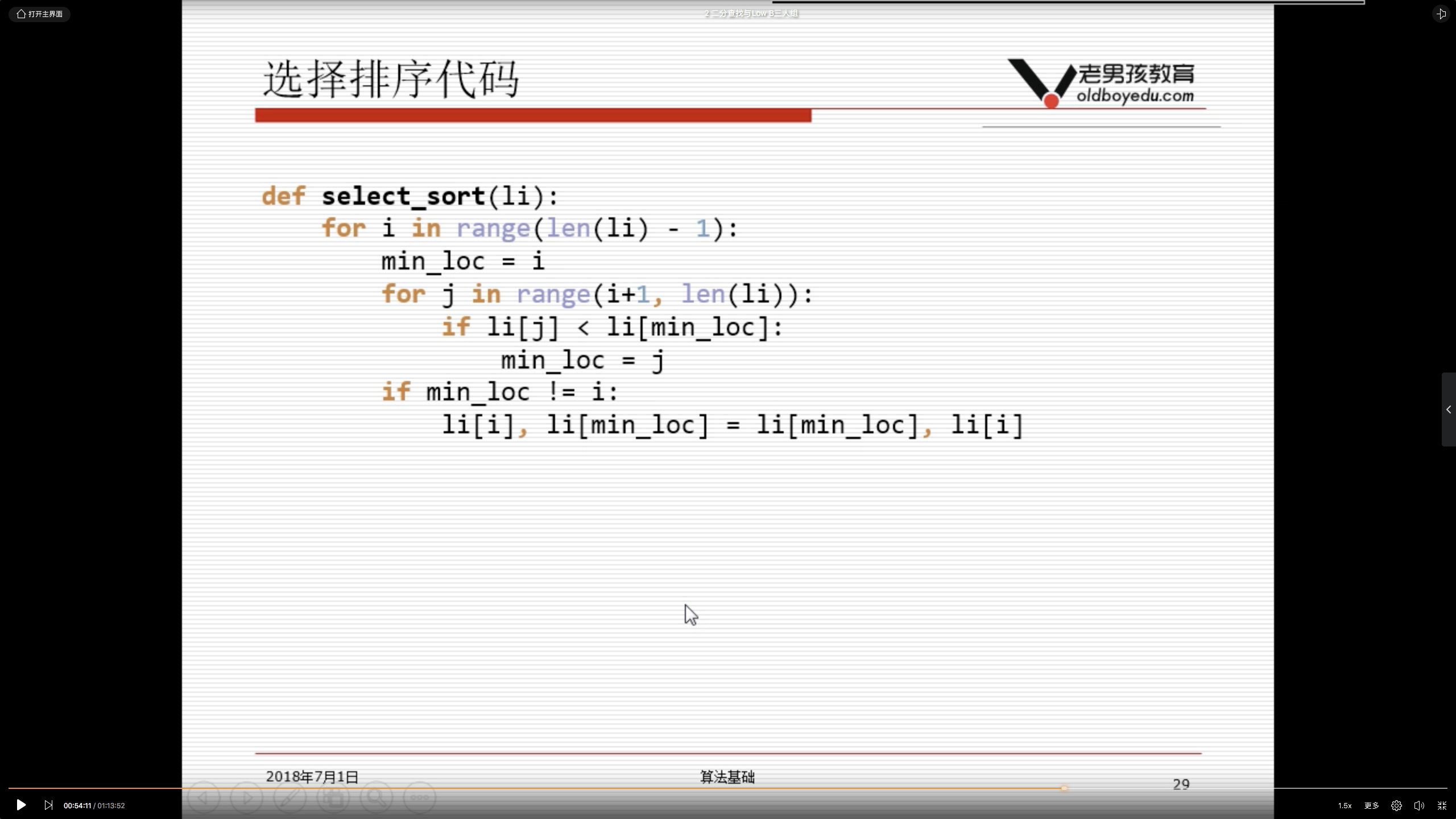
2.5 选择排序思路

• 代码关键点——无序区域、最小数的位置；

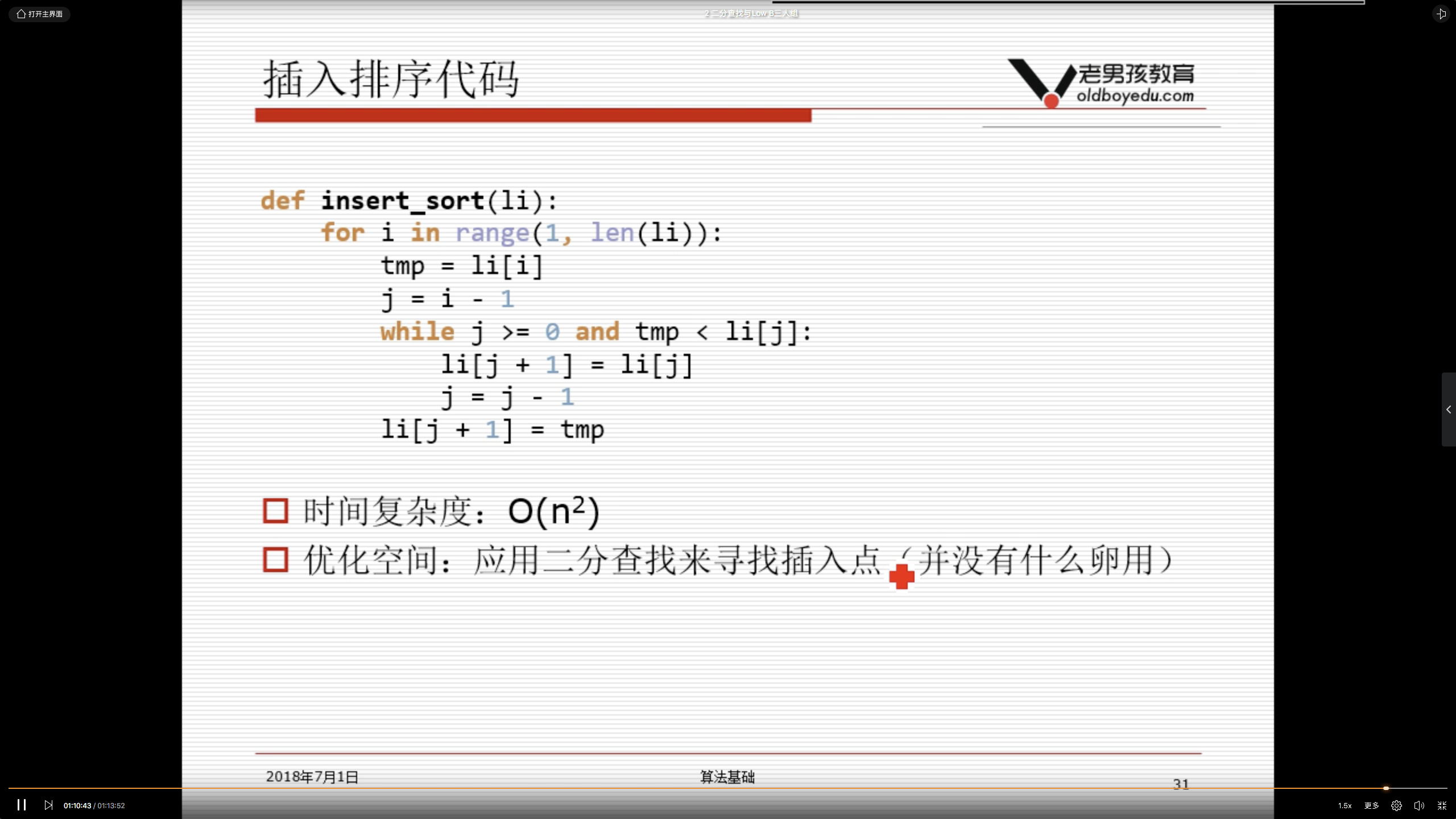
2.6 插入排序；

03 快速排序

04 堆排序

05 归并排序