数学图形(2.14)Spherical helix曲线

从http://mathworld.wolfram.com/SphericalHelix.html上找到如下一些关于该曲线的说明,不过似乎他的公式和我的脚本完全是两个东西..

The tangent indicatrix of a curve of constant precession is a spherical helix. The equation of a spherical helix on a sphere with radius 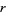 making an angle  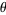with the z-axis is

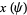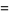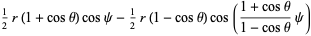			(1)
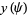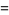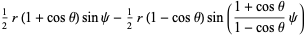			(2)
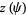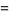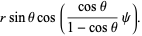			(3)

The projection on the 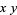-plane is an epicycloid with radii

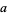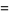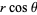			(4)
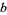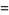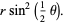			(5)

#http://www.mathcurve.com/courbes3d/helicespheric/helicespheric.shtml

vertices = 

t = from  to (*PI)

k = rand2(0.0, )

s = sin(t)
c = cos(t)

a = sin(k*t)
b = cos(k*t)

r = 

x = r*(k*c*b - s*a)
z = r*(k*s*b + c*a)
y = r*sqrt( - k*k)*b