【Python算法】图与树的实现

邻接列表及其类似结构

　　对于图结构的实现来说，最直观的方式之一就是使用邻接列表。下面我们来实现一个最简单的：假设现在我们有n个节点，编号分别为0，...，n-1。

　　然后，每个邻接列表就是一个数字列表，我们可以将他们编入一个大小为n的主列表，并用节点编号对其进行索引。

　　

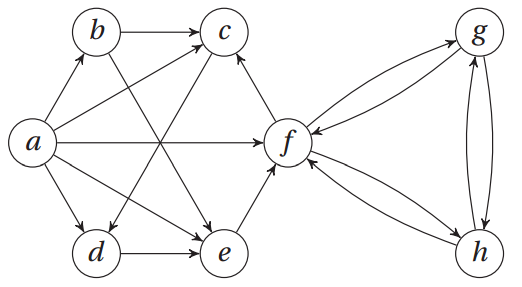
　　邻接集表示法：

a, b, c, d, e, f, g, h = range(8)
N = [
 {b, c, d, e, f},        # a
 {c, e},                 # b
 {d},                    # c
 {e},                    # d
 {f},                    # e
 {c, g, h},              # f
 {f, h},                 # g
 {f, g}                  # h
]

　　邻接列表

a, b, c, d, e, f, g, h = range(8)
N = [
 [b, c, d, e, f],        # a
 [c, e],                 # b
 [d],                    # c
 [e],                    # d
 [f],                    # e
 [c, g, h],              # f
 [f, h],                 # g
 [f, g]                  # h
]

　　加权邻接字典

a, b, c, d, e, f, g, h = range(8)
N = [
 {b:2, c:1, d:3, e:9, f:4},   # a
 {c:4, e:3},                  # b
 {d:8},                       # c
 {e:7},                       # d
 {f:5},                       # e
 {c:2, g:2, h:2},             # f
 {f:1, h:6},                  # g
 {f:9, g:8}                   # h
]

邻接矩阵

　　嵌套 list 实现的邻接矩阵

a, b, c, d, e, f, g, h = range(8)
# a b c d e f g h
N = [[0,1,1,1,1,1,0,0], # a
     [0,0,1,0,1,0,0,0], # b
     [0,0,0,1,0,0,0,0], # c
     [0,0,0,0,1,0,0,0], # d
     [0,0,0,0,0,1,0,0], # e
     [0,0,1,0,0,0,1,1], # f
     [0,0,0,0,0,1,0,1], # g
     [0,0,0,0,0,1,1,0]] # h

　　由于图上没有自循环状态，其对角线上的值应该全为假。

　　无向图的邻接矩阵应该是一个对称矩阵。

　　我们通常会把不存在的边的权值设置为无穷大。

inf = float('inf')
a, b, c, d, e, f, g, h = range(8)
# a b c d e f g h
N = [[inf, 1 , 1 , 1 , 1 , 1 ,inf,inf], # a
     [inf,inf, 1 ,inf, 1 ,inf,inf,inf], # b
     [inf,inf,inf, 1 ,inf,inf,inf,inf], # c
     [inf,inf,inf,inf, 1 ,inf,inf,inf], # d
     [inf,inf,inf,inf,inf, 1 ,inf,inf], # e
     [inf,inf, 1 ,inf,inf,inf, 1 , 1 ], # f
     [inf,inf,inf,inf,inf, 1 ,inf, 1 ], # g
     [inf,inf,inf,inf,inf, 1 , 1 ,inf]] # h

　　在邻接矩阵中，查询变（u,v）需要的时间为Θ（1），遍历v邻居的操作时间为Θ（n）；

　　邻接列表中，两种操作所需的时间都为Θ（d（v））

　　我们应该根据图的具体用处来选择相关的表示法。

树的实现

　　

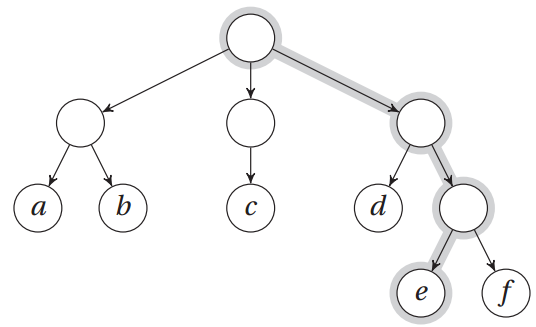
　　树表示成一个二维列表

>>> T = [["a", "b"], ["c"], ["d", ["e", "f"]]]
>>> T[0][1]
'b'
>>> T[2][1][0]
'e'

　　二叉树类：

class Tree:
　　def __init__(self, left, right):
　　self.left = left
　　self.right = right

>>> t = Tree(Tree("a", "b"), Tree("c", "d"))
>>> t.right.left
'c'

　　

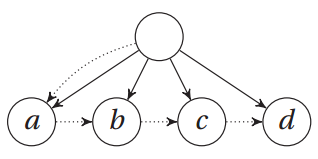
　　多路搜索树类：

class Tree:
    def __init__(self, kids, next=None):
    self.kids = self.val = kids
    self.next = next

>>> t = Tree(Tree("a", Tree("b", Tree("c", Tree("d")))))
>>> t.kids.next.next.val
'c'

　　Bunch模式：

class Bunch(dict):
    def __init__(self, *args, **kwds):
    super(Bunch, self).__init__(*args, **kwds)
    self.__dict__ = self

>>> T = Bunch
>>> t = T(left=T(left="a", right="b"), right=T(left="c"))
>>> t.left
{'right': 'b', 'left': 'a'}
>>> t.left.right
'b'
>>> t['left']['right']
'b'
>>> "left" in t.right
True
>>> "right" in t.right
False