算法 UVA 11292

***从今天开始自学算法。

***代码是用c++,所以顺便再自学一下c++

例题1  勇者斗恶龙（The Dragon of Loowater, UVa 11292）

你的王国里有一条n个头的恶龙，你希望雇一些骑士把它杀死（即砍掉所有头）。村里有m个骑士可以雇佣，一个能力值为x的骑士可以砍掉恶龙一个直径不超过x的头，且需要支付x个金币。如何雇佣骑士才能砍掉恶龙的所有头，且需要支付的金币最少？注意，一个骑士只能砍一个头（且不能被雇佣两次）。

【输入格式】

输入包含多组数据。每组数据的第一行为正整数n和m（1≤n,m≤20 000）；以下n行每行为一个整数，即恶龙每个头的直径；以下m行每行为一个整数，即每个骑士的能力。输入结束标志为n=m=0。

【输出格式】

对于每组数据，输出最少花费。如果无解，输出“Loowater isdoomed!”。

【样例输入】

2 3

5

4

7

8

4

2 1

5

5

10

0 0

【样例输出】

11

Loowater is doomed!

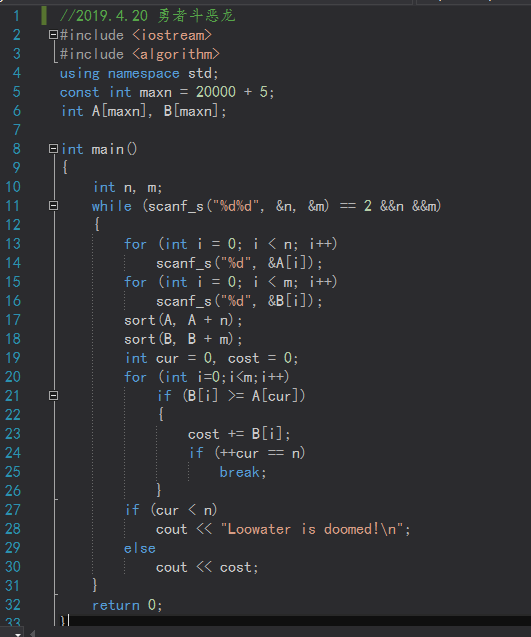
【分析】
能力强的骑士开价高是合理的，但如果被你派去砍一个很弱的头，就是浪费人才了。因此，可以把雇佣来的骑士按照能力从小到大排序，所有头按照直径从小到大排序，一个一个砍就可以了。当然，不能砍掉“当前需要砍的头”的骑士就不要雇佣了