机器学习(2)：Softmax回归原理及其实现

Softmax回归用于处理多分类问题，是Logistic回归的一种推广。这两种回归都是用回归的思想处理分类问题。这样做的一个优点就是输出的判断为概率值，便于直观理解和决策。下面我们介绍它的原理和实现。

1.原理

a.问题

考虑\(K\)类问题，假设已知训练样本集\(D\)的\(n\)个样本\(\{(x_{i},t_{i})| i=1,...,n\}\) ，其中，\(x_i \in R^d\) 为特征向量，\(t_{i} \) 为样本类别标签，和一般而分类问题不同，Softmax回归采用了标签向量来定义类别，其定义如下：

\(t_{i}=\begin{pmatrix}
0\\
\vdots \\
1\\
\vdots\\
0
\end{pmatrix}\begin{matrix}
0\\
\vdots\\
k\\
\vdots\\
K
\end{matrix}\)    -------------------（1）

标签向量为0 − 1的\(K\)维向量,若属于\(k\)类,则向量的\(k\)分量为1,其他分量均为0

为计算每个样本的所属类别概率，首先定义回归函数：

\(p(C_{k}|x)=\frac{exp(w_{k}^{T}x)}{\sum_{k=1}^{K}exp(w_{k}^{T}x)}\) -------------------（2）

其中\(w_{k}\) 为第\(k\)类的回归参数。根据回归函数，样本\(x_{i}\)的概率：

\(p(x_{i}|w_{1} , ... , w_{K})=\prod_{k=1}^{K}p(C_{k}|x)^{t_{ik}}\)-------------------（3）

其中,\(t_{i} = (t _{i1} , ... , t _{ik} , ... , t _{iK})^{T}\)为\(x\)的标签向量。

我们的目标是：估计回归参数\(w_{1} , ... , w_{K}\)。用什么办法呢，极大似然估计法。

b.算法

i)构造目标函数

我们采用极大似然法估计回归参数\(w_{1} , ... , w_{K}\)。我们的目标是期望所有样本的获得概率最大化，因此构造如下似然函数：

\((P(D|w_{1} , ... , w_{K})=\frac{1}{n}\prod_{i=1}^{n}\prod_{k=1}^{K}p(C_{k}|x)^{t_{ik}}\)-------------------（4）

为了计算方便，对以上似然函数取负对数，将问题转化为最小化问题，从而最优化问题的目标函数为：

\(\underset{w_1,...,w_K}{min}E(w_1,...,w_K) \)-------------------（5）

其中

\(E(w_{1} , ... , w_{K})=\frac{1}{n}\sum_{i=1}^{n}\sum_{k=1}^{K}t_{ik}\textbf{ln}p(C_{k}|x)\)

ii)梯度下降法

求解算法许多，这里我们考虑采用梯度下降迭代法，主要解决梯度和步长的问题，第\(k\)个回归参数\(w_k\)的更新迭代公式如下：

\(w_{k}^{new}=w_{k}^{old}-\lambda\frac{\partial E}{\partial w_k}\)   -------------------（6）

其中\(\lambda\)步长，即学习率，\(\frac{\partial E}{\partial w_k}\)为关于\(w_k\)的梯度，具体计算公式如下：

\(\frac{\partial E}{\partial w_k}=-\frac{1}{n}\left [ \sum_{i=1}^{n}\left ( t_{ik}-P(C_k|x_i) \right )x_i \right ]\)  -------------------（7）

对梯度加入权重因此会获得更好的效果，因此（2）可改进为：

\(\frac{\partial E}{\partial w_k}=-\frac{1}{n}\left [ \sum_{i=1}^{n}\left ( t_{ik}-P(C_k|x_i) \right )x_i \right ] + \lambda w_k\)  -------------------（8）

梯度技巧提示：求解单个分量的梯度，然后在整合成向量表示形式。

提示：梯度求解需要复合梯度求导，对数求导以及\(\frac{x}{x+a}\)的求导，例如:

链式求导法则：若\(h(x)=f(g(x))\)，则\({h}'(x)={f}'(g(x)){g}'(x)\)

对数：\({lnx}'=\frac{1}{x}\)

分数：\({(\frac{x}{x+a})}'=\frac{a}{(x+a)^2}\)

2.实现

我们将根据公式（2）和（8），利用python实现Softmax回归。先看随着迭代，精度变化的趋势图，如下图所示：

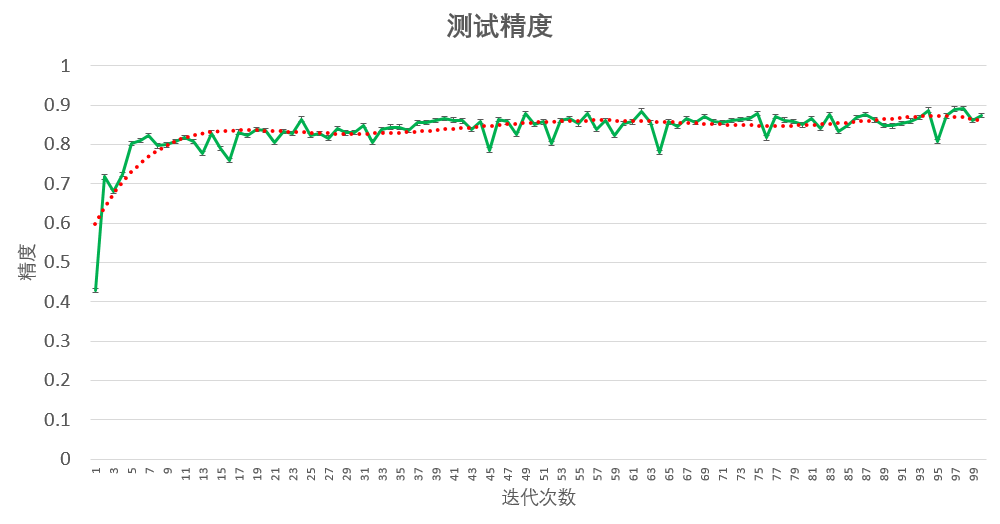
精度在迭代开始不久就收敛到很好的结果，但后期会出现较大的波动，可见其收敛并不理想，要达到90%的精度，就需要更久的迭代次数了，比如十万次迭代等。改进的手段是改进特征的描述。深度学习就可以很好的学习特征的算法。

最后贴上码农最爱的代码（修改自《python 实现 softmax分类器（MNIST数据集）》）：

# encoding=utf8
'''
Created on 2017-7-1

@author: Administrator
'''

import random
import time
import math
import pandas as pd
import numpy as np

from sklearn.model_selection import train_test_split as ttsplit
from sklearn.metrics import accuracy_score as eva_score
from matplotlib import pyplot as plt

class SoftMaxRegression(object):
    '''
    Softmax回归分类器
    '''

    def __init__(self, learning_step=0.000001 ,max_iteration=100000,weight_lambda=0.01,iseva = True):
        '''
        构造函数
        '''
        self.learning_step = learning_step           # 学习速率
        self.max_iteration = max_iteration           # 最大迭代次数
        self.weight_lambda = weight_lambda           # 衰退权重
        self.iseva = iseva                           # 是否评估
    def cal_e(self,x,l):
        '''
        计算指数：exp(wx)
        '''

        theta_l = self.w[l]
        product = np.dot(theta_l,x)

        return math.exp(product)

    def cal_probability(self,x,k):
        '''
        计算样本属于第k类的概率，对应公式（2）
        '''

        molecule = self.cal_e(x,k)
        denominator = sum([self.cal_e(x,i) for i in range(self.K)])

        return molecule/denominator

    def cal_partial_derivative(self,x,y,k):
        '''
        计算第k类的参数梯度，对应公式（8）
        '''

        first = int(y==k)                           # 计算示性函数
        second = self.cal_probability(x,k)          # 计算后面那个概率

        return -x*(first-second) + self.weight_lambda*self.w[k]

    def predict_(self, x):
        '''
        预测测试样本
        '''
        result = np.dot(self.w,x)
        row, column = result.shape

        # 找最大值所在的列
        _positon = np.argmax(result)
        m, n = divmod(_positon, column)

        return m

    def train(self, features, labels, test_features=None, test_labels=None):
        '''
        训练模型
        '''
        self.K = len(set(labels))

        self.w = np.zeros((self.K,len(features[0])+1))
        time = 0
        self.score = []
        while time < self.max_iteration:
            #print('loop %d' % time)
            time += 1
            index = random.randint(0, len(labels) - 1)

            x = features[index]
            y = labels[index]

            x = list(x)
            x.append(1.0)
            x = np.array(x)
            #计算每一类的梯度
            derivatives = [self.cal_partial_derivative(x,y,k) for k in range(self.K)]

            for k in range(self.K):
                self.w[k] -= self.learning_step * derivatives[k]#负梯度为下降最快的方向

            if self.iseva == True and time%1000 == 0:
                self.acc_score(test_features, test_labels)   

        return self.score
    def predict(self,features):
        '''
        预测测试样本集
        '''
        labels = []
        for feature in features:
            x = list(feature)
            x.append(1)

            x = np.matrix(x)
            x = np.transpose(x)

            labels.append(self.predict_(x))
        return labels

    def acc_score(self,test_features,test_labels):
        '''
        评估精度
        '''
        label_predict = self.predict(test_features)
        predict_score = eva_score(test_labels, label_predict)
        print predict_score

        self.score.append(predict_score)

if __name__=='__main__':

    print("Import data")
    raw_data = pd.read_csv('../data/train.csv', header=0)
    data = raw_data.values
    imgs = data[0::, 1::]
    labels = data[::, 0]
    train_features, test_features, train_labels, test_labels = ttsplit(
        imgs, labels, test_size=0.33, random_state=23323)
    print train_features.shape
    print test_features.shape  

    print("Training model")
    learning_step = 0.000001            # 学习速率
    max_iteration = 100000              # 最大迭代次数
    weight_lambda = 0.01                # 衰退权重
    iseva = True                        # 是否评估
    smr = SoftMaxRegression(learning_step,max_iteration,weight_lambda,iseva)
    scores = smr.train(train_features, train_labels,test_features,test_labels)
    print scores
    #print("Predicting model")
    #test_predict = smr.predict(test_features)

    #print("Envaluate model")
    #score = accuracy_score(test_labels, test_predict)
    #print("The accruacy socre is " + str(score))

    print("Plot accuracy")
    idx = range(len(scores))

    plt.plot(idx,scores,color="b",linewidth= 5)

    plt.xlabel("iter",fontsize="xx-large")
    plt.ylabel("accuracy",fontsize="xx-large")
    plt.title("Test accuracy")
    plt.legend(["testing accuracy"],fontsize="xx-large",loc='upper left');
    plt.show()

请参考推导及伪代码：softmax的简单推导和python实现

3.参考资料

[1].DeepLearning之路（二）SoftMax回归