人工智能——搜索（1）回溯策略【N皇后问题】

这学期学《人工智能》（马少平，朱小燕　编著）这本书，里面很多算法听老师讲都听不懂，就想试试写一下看看能不能写出来，就从最简单的回溯策略开始吧。

源码

---

题目描述

在一个n*n的国际象棋棋盘上，一次一次地摆布n枚皇后，摆好后要满足每行、每列和对角线上只允许出现一枚棋子，即棋子间不许互相俘获。

解题思路

使用用递归的方式实现回溯，每一行从左到右填，填不下去就回溯到上一行。

以四皇后为例

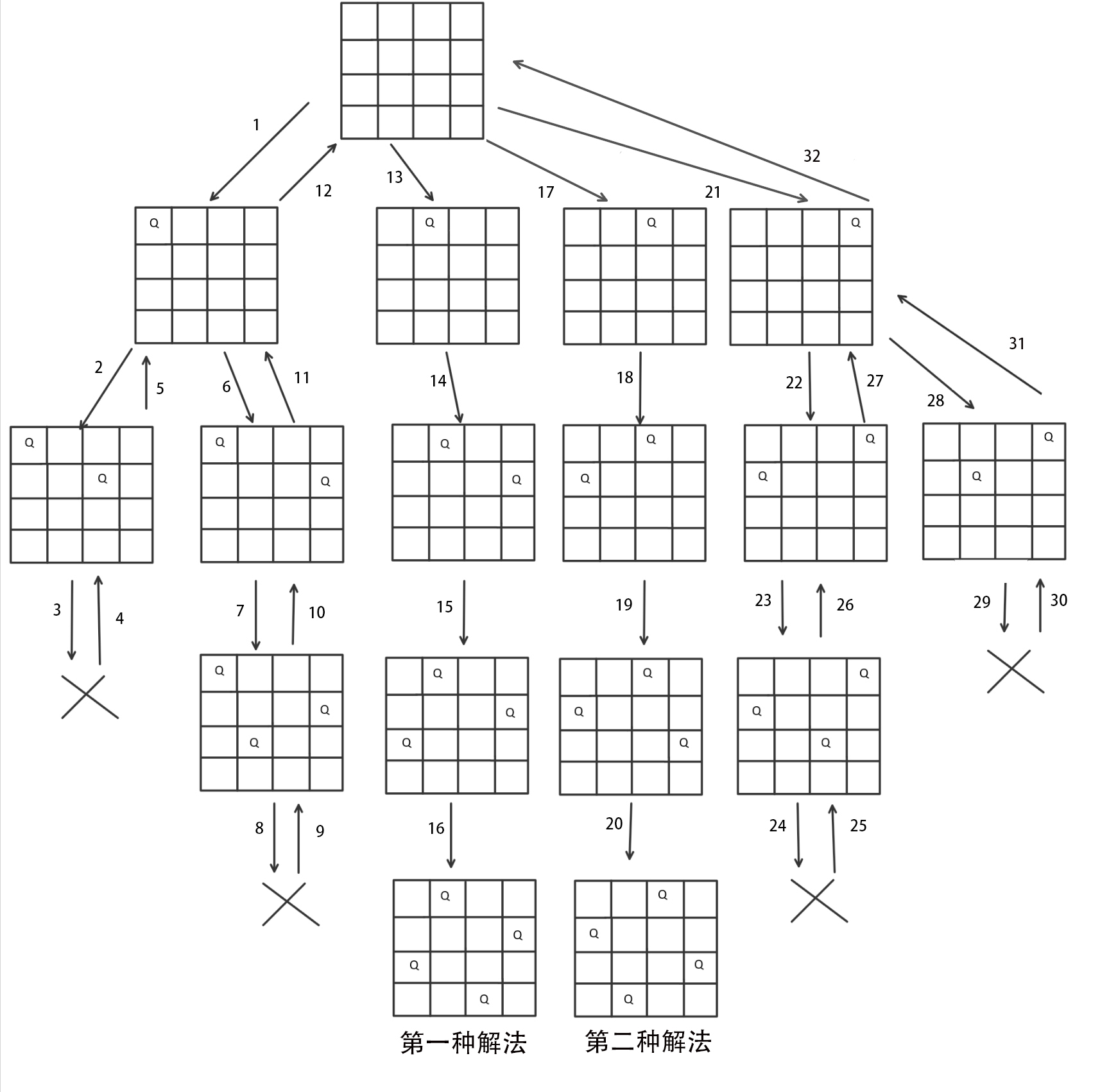
代码实现

递归函数，如果能放下皇后且还没到最后一行，递归进入下一行。

void Nqueens(int num)
{
    int i;
	for(i=1;i<=n;i++)
	{
		queen[num]=i;
		if(CanPlace(queen,num))
		{
			if(num==n)
                Output();
			else
                Nqueens(num+1);
		}
	}
}

判断是否能放皇后,可以把已经放下的和现在放的相比，因为我是一行一行填，所以只要判断列和对角线有没有重复。用一个queen数组记录每行的皇后放的位置，行减行的绝对值和位置减位置的绝对值相等时在同一对角线，位置相等时在同一列。

bool CanPlace(int queen[],int num)
{
    int i;
	for(i=1;i<num;i++)
	{
		if(abs(queen[i]-queen[num])==abs(i-num) || queen[i]==queen[num])
			return false;
	}
	return true;
}

性能分析

耗时最多的是取绝对值函数，如果能找到比用绝对值更好的判断方法，程序就能更快。

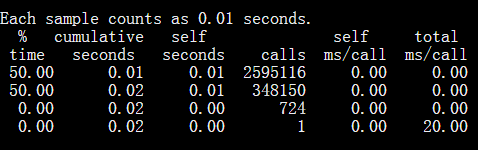
总结

回溯策略是盲目搜索的一种，而用递归法是最直接的实现方法，处理皇后问题效率还不错，后面可能会写写启发式搜索（看得懂的话就写）。