OI字符串简单学习笔记

持续更新qwq

KMP

其实是MP啦qwq

就是先自己匹配自己得到状态图，然后再在上面进行模式串的匹配。

nxt数组返回的是以该节点结尾的，最长的，在前面出现过的，不相交的，字符串的最靠右的，末位位置。

举个例子：对于字符串aabaabaabaab来说，它的nxt数组是这个样子的——

nxt[0]=0,nxt[1]=0,nxt[2]=1,nxt[3]=0,nxt[4]=1,nxt[5]=2,nxt[6]=3,nxt[7]=4,nxt[8]=5,nxt[9]=6,nxt[10]=7,nxt[11]=8

以下是模板啦qwq

#include<iostream>

#include<cstdio>

#include<algorithm>

#include<cstring>

#define MAXN 1000010

using namespace std;

int nxt[MAXN],kmp[MAXN];

char s1[MAXN],s2[MAXN];

int main()

{

    cin>>(s1+1);

    cin>>(s2+1);

    int len1=strlen(s1+1),len2=strlen(s2+1);

    int j=0;

    for(int i=2;i<=len2;i++)

    {

    	while(j&&s2[j+1]!=s2[i]) j=kmp[j];

    	if(s2[j+1]==s2[i]) j++;

    	kmp[i]=j;

    }

    j=0;

    for(int i=1;i<=len1;i++)

    {

        while(j&&s2[j+1]!=s1[i]) j=kmp[j];

        if(s2[j+1]==s1[i])  j++;

        if(j==len2)

        {

            printf("%d\n",i-len2+1);

            j=kmp[j];

        }

    }

    for(int i=1;i<=len2;i++) printf("%d ",kmp[i]);

    return 0;

}

SA后缀数组

以下是蒟蒻自己写的注释的模板qwq（没有height数组）（输入一个字符串，依次输出排名为i的字符串所在位置）

#include<iostream>

#include<cstdio>

#include<algorithm>

#include<cstring>

#define MAXN 1000010

using namespace std;

int n,m,p;

int tax[MAXN],rnk[MAXN],tp[MAXN],sa[MAXN];

char s[MAXN];

inline void qsort()

{

    for(int i=1;i<=m;i++) tax[i]=0;

    //tax[i]表示排名为i的后缀的个数

    for(int i=1;i<=n;i++) tax[rnk[i]]++;//累加排名为rnk[i]的个数

    for(int i=1;i<=m;i++) tax[i]+=tax[i-1];//求前缀和

    for(int i=n;i>=1;i--) sa[tax[rnk[tp[i]]]--]=tp[i];

    //现在tp数组和rnk数组已经有序了，所以我们现在要用它们来更新sa

}

inline void suffixsort()

{

    m=75,p=0;

    //m是字符集的个数，下文中用p来计数

    for(int i=1;i<=n;i++) rnk[i]=s[i]-'0'+1,tp[i]=i;

    qsort();

    for(int w=1;p<n;w<<=1,m=p)

    {

        p=0;

        //一定要记得p的清零，现在它是一个计数的作用

        for(int i=1;i<=w;i++) tp[++p]=n-w+i;//现在处理的是后面不能配对的位置的第二关键字的排名

        //这些位置的第二关键字为0，都相等。但是为什么++p了，因为这里计算的是第二关键字的个数

        for(int i=1;i<=n;i++) if(sa[i]>w) tp[++p]=sa[i]-w;//现在处理的可以配对的第二关键字的排名

        qsort();

        swap(tp,rnk);

        //我们要用上个rnk更新现在rnk

        rnk[sa[1]]=p=1;

        //初始化

        for(int i=2;i<=n;i++) rnk[sa[i]]=(tp[sa[i]]==tp[sa[i-1]])&&(tp[sa[i]+w]==tp[sa[i-1]+w])?p:++p;

        //当第一，第二关键字的排名相同的时候 显然现在的rnk也是一样的

        //现在p表示的是不同排名的个数，如果p==n就可以结束了

    }

}

int main()

{

    freopen("ce.in","r",stdin);

    scanf("%s",s+1);

    n=strlen(s+1);

    suffixsort();

    for(int i=1;i<=n;i++) printf("%d ",sa[i]);

    return 0;

}

SAM后缀自动机

以下内容摘抄自这里

inline void extend(int c)

{

    int p=last,np=++tot;last=np;

    t[np].len=t[p].len+1;

    while(p&&!t[p].son[c]) t[p].son[c]=np,p=t[p].ff;

    if(!p)t[np].ff=1;

    else

    {

        int q=t[p].son[c];

        if(t[p].len+1==t[q].len) t[np].ff=q;

        else

        {

            int nq=++tot;

            t[nq]=t[q];

            t[nq].len=t[p].len+1;

            t[q].ff=t[np].ff=nq;

            while(p&&t[p].son[c]==q) t[p].son[c]=nq,p=t[p].ff;

        }

     }

}

endpos

endpos是一个子串结束为止组成的集合。

对于所有结束位置相同的字串，也就是endpos相同的两个子串。他们一个一定是另一个的后缀

两个字符串如果有一个是另一个的后缀，那么较长串的后缀一定是较短串的endpos的子集

两个字符串如果没有后缀的关系，那么他们的endpos的交集一定是空集

后缀自动机的每个节点是依照endpos来划分的，对于endpos相同的子串，我们可以划分在一起。所以我们不难得出一点，对于一堆endpos相同的子串，他们一定互为后缀，并且他们的长度连续。

既然后缀连续，那就一定有一个最长的串，不妨记为longest。那么，所有的其他串一定是它的后缀。随着后缀长度的减小，那么从某一个后缀开始，就可能出现在了更多的位置。那么买这个后缀以及比它更短的后缀的endpos一定会变大，此时他们就会分到别的节点去了。

确定了endpos和长度len就能确定唯一的子串

trans

trans是转移的意思，设trans(s,c)表示当前在s状态，接受一个字符c之后所到达的状态。一个状态s表示若干endpos相同的连续子串。

那么此时相当于在后面加上了一个字符c。那么我们对于任意一个串直接加上一个字符c之后，组成的串的endpos还是相同的。所以trans(s,c)就会指向这个状态。

parent/suffix links

不妨设一个状态中包含的最短的串叫做shortest。那么我们就知道shortest的任意一个非自己的后缀一定就会出现在了更多的位置。它的那个最长的后缀，也就是减去了第一个字符后的串，就会出现在另外一个状态里，并且是那个状态的longest。

parent tree上，每一个点集的父亲都是自己的后缀。也就是说,沿着suffix_link向上跳,会一直跳到自己的后缀(不过当然,它们不在一个endpos里面)

假设当前状态为s，$s.shortest.len=parent.longest.len+1$

所以对于每个状态，没有必要记录shortest，因为你只要知道parent就可以算出来了。

s的endpos是parent的子集

这个不难证明，因为parent包含了更多的位置。

如果trans(s,c)不等于NULL，那么trans(parent,c)不等于NULL

parent是一个完全包含了s的状态，也正因为如此，parent的endpos就是所有儿子endpos的并集

将所有的parent翻过来，我们就得到了parent树。如果要处理什么，就需要parent树的拓扑序。（因为parent相当于包含了它的所有子树，都需要更新上去）。。。不过其实不需要拓扑排序，我们知道s的endpos完全被parent的endpos包含，所以s.longest一定长于parent.longest。所以一个状态的longest越长，它一定要被更先访问。所以，按照longest的长度进行桶排序就可以解决拓扑序了。

extend

对于一个SAM的构造，我们依次加入字符c，来进行构造。

假设原来的字符串是T，首先一定会有一个新节点。因为新加入了一个字符后，一定出现了这个新的字符T+c。此时的endpos一定是新的位置。同时，原来的T的最后一个位置也可以通过+c变到这个新位置。设原来的最后一个位置的状态是last，新的状态是np。所以tans(last,c)=np。

根据前面的东西，我们知道last的祖先们一定也会有这个trans，之后来解决这个问题——

令p=last，一直沿着parent往前跳，也就是不断令$p=p.parent$,所以p所代表的的，就是越来越短的T的后缀。因为要更新的是最后的位置。只有当存在T的最后一个位置的时候才能更新。

如果$trans(p,c)=NULL$，直接令$tans(p,c)=np$。很显然是可以在后面添加一个c到达np的，如果跳完之后发现没有parent了，直接把np.parent指向1（也就是空串所代表的状态）

如果某个$trans(p,c)$不等于NULL，那么设$q=trans(p,c)$——

如果有$longest(p)+1=longest(q)$，那么我们在p的串后面直接添上一个c之后就是q状态。没有任何问题，直接在作为T的后缀的那一个子串上，直接添加一个x显然也可以到达q状态，又因为np所代表的endpos更小，所以$np.parent=q$。

否则的话，也就是$longest(q)>longest(p)+1$（也就是前面那个while更新的时候可能会导致的情况）。如果直接插入的话，相当于给q的endpos强行插入一个np,但是我们发现，如果强行插入进去，这个T+c的后缀会出现在更多的位置，应该属于另外一个状态，不太行。

所以我们新建一个节点nq，相当于把q拆成两部分：一部分是T+c的那个后缀，一个是$longest(p)+c$，也就是$longest(nq)=longest(p)+1$，显然T+c的后缀是包含了状态较少的，拆分出来的一部分q是长度较长的。所以$q.parent=np.parent=nq$。同时，继续沿着p的parent往上走，把所有的q都替换成nq。

也就是这样——

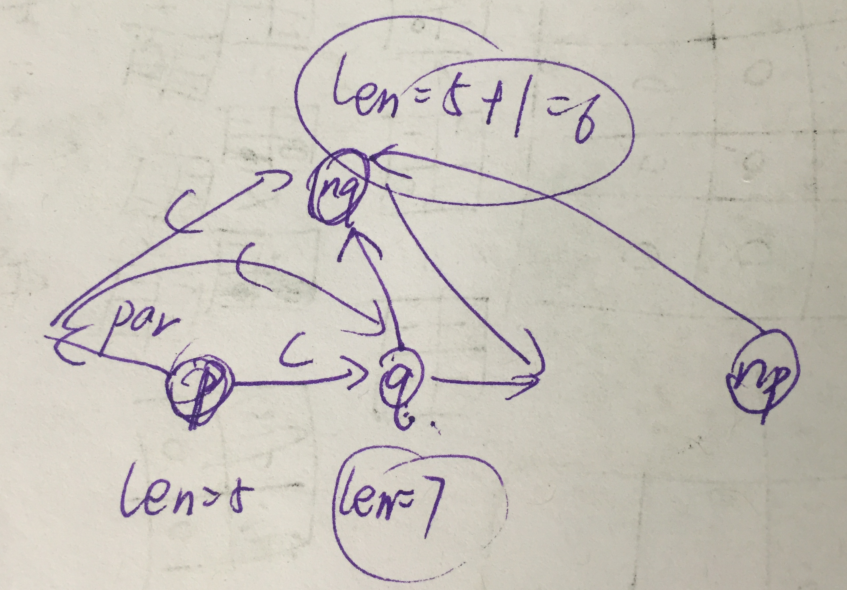
SAM里面有两种节点，一种是直接建出来，另外一种是分裂出来的。

last表示的是新建的那个节点。

一个节点可以表示一个类，里面有很多子串，他们的 endpos相同。

比如对于字符串S="aabbabd"，它的后缀自动机是：

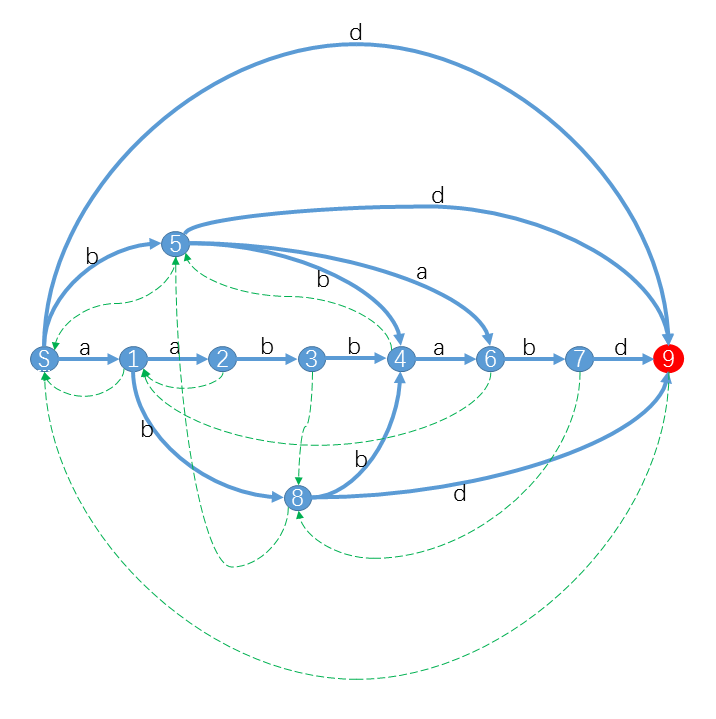
至于空间问题，开处理的字符串长度的两倍就行了qwq

如果只要求解right集合大小的话，直接基数排序一下，按照拓扑序向上合并即可。

如果要求right集合，线段树向上合并维护。

两个后缀的最长公共前缀是他们在parent tree上面LCA的len

两个前缀的最长公共后缀是他们在后缀树上面LCA的len