线性回归，感知机，逻辑回归（GD，SGD）

线性回归

线性回归是一个回归问题，即用一条线去拟合训练数据

线性回归的模型： 通过训练数据学习一个特征的线性组合，以此作为预测函数。

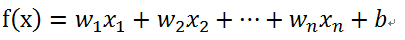
训练目标：根据训练数据学习参数(w₁,w₂, ... , w_n,b)

学习策略：

要确定参数(w₁,w₂, ... , w_n,b)，即关键在于如何衡量 预测函数f(x)与训练数据y之间的差别。

     如果要使得预测函数f(x)尽可能准确，那么即要求f(x)-y尽可能小，而f(x)-y便是一个样本（x,y）的损失函数。

对于整个训练数据的损失函数，用均方误差损失函数（1/2是为了求导方便）

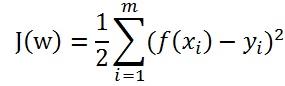
即当均方误差损失函数J最小时的参数(w₁,w₂, ... , w_n,b)，便是最终线性模型中的参数。

所以目标就是求:

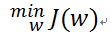
求解这个损失函数的方法主要有两个： 最小二乘法，梯度下降法

---

使用梯度下降法求解  （梯度下降，批量梯度下降，随机梯度下降）

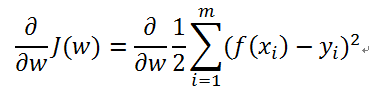
我们知道曲面上沿着梯度的方向是函数值变化（增大）最快的方向，因此要得到J(w)最小值，应该沿着梯度的反方向。

使用沿着梯度的反方向进行权重的更新，可以有效的找到全局的最优解。

更新过程如下：

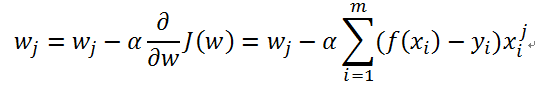
说明：

1. 上述是对参数向量W的分量w_j进行更新的表达式。由更新表达式可知，每次更新使用所有的训练数据（m个样本）。

2. 在对参数w_j更新时，使用到了样本x_i（样本x_i是个向量）的第j个分量。

3. 使用类似上面的表达式同时更新参数向量W的每一个分量，即更新参数向量W。

4. 更新参数时为什么使用 参数当前值 - 步长和导数的乘积？

更新参数时应该是 参数当前值 + 步长和导数的乘积，但是由于曲面上沿着梯度的方向是函数值变化（增大）最快的方向，而我们求函数值减小最快的方向，因此应该给梯度方向取反

       因此更新表达式为 参数当前值 - 步长和导数的乘积。

5. 未写出b的更新表达式，实质上可将参数W拓展，将b包含进W之中，更新过程是相同的。

参数拓展：w=(w₁, w₂, ... , w_n, b)  ，x=(x₁, x₂, ... , x_n, 1)

---

梯度下降，批量梯度下降，随机梯度下降 

• 梯度下降：W的每一次更新，使用所有的样本。计算得到的是一个标准梯度。更新一次的幅度较大，样本不大的情况，收敛速度可以接受；但是若样本太大，收敛会很慢。

• 随机梯度下降：随机 --- 每次使用训练数据中的一个样本更新，因而随机梯度下降是会带来一定的问题，因为计算得到的并不是准确的一个梯度，容易陷入到局部最优解中。

• 批量梯度下降：批量的梯度下降就是一种折中的方法，他用了一些小样本来近似全部的样本。即：每次更新w使用一批样本。

• 步长的选择： 
  • 步长太小，收敛速度太慢
  • 步长太大，会在最佳收敛点附近徘徊

---

感知机

感知机是一个二分类问题

感知机模型：

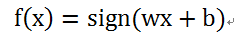
 说明：

　　1. 上式中的w和x，都表示向量。w=(w₁, w₂, ... , w_n)  ，x=(x₁, x₂, ... , x_n)

　　2. 感知机的（wx+b）可以理解为线性回归，即感知机将线性回归的输出 作为使用单位阶跃函数的输入，最终的分类结果是阶跃函数的输出。

训练目标：根据训练数据学习参数(w₁,w₂, ... , w_n,b)

学习策略：误分类点到分类超平面的总距离

---

对于超平面wx+b=0，w是垂直于超平面的法向量，因此

点到超平面的距离:

误分类点到超平面的距离：（误分类说明预测的分类 (wx+b)和实际分类不一致，因此乘积为-1，而距离是绝对值，所以应该是 -y(wx+b)）

---

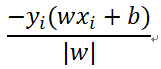
损失函数：误分类点到超平面（wx+b=0）的总距离(未考虑前面的参数1/|w|)

即当损失函数L(w,b)最小时的参数(w₁,w₂, ... , w_n,b)，便是最终模型中的参数。

所以目标就是求:

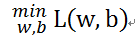
可以使用梯度下降法，更新参数w，b。类似于线性回归中的方法，可以拓展参数向量w=(w,b)

梯度：

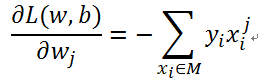
更新过程:

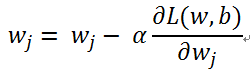
说明：

1. 上述M是误分类点的集合，每次使用一批样本更新参数

2. w_j表示参数向量w的第j个分量

3. 使用样本x_i的第j个分量 更新参数w_j

---

逻辑回归

逻辑回归是一个二分类问题

逻辑回归模型：

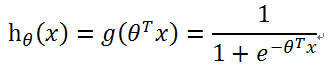
说明：本质是将线性回归的输出作为sigmoid函数的输入，最终的输出便是分类的结果。

模型解释：对于给定的x，输出y=1的概率

训练目标：根据训练数据学习参数

学习策略：条件概率p(y|x),表示x是输入，y是正确的输出的概率。学习策略即为求所有训练样本的条件概率之积的最大值。即要求概率之积尽可能大，这样模型的预测效果就会越准确。

损失函数：对数似然损失函数

---

对于y=1 以及y=0有下列概率：

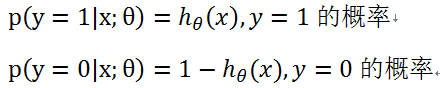
因此，综合以上两种情况：

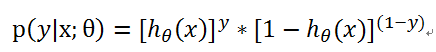
损失函数原始形式：

（L表示所有训练样本的条件概率之积）

取对数得到损失函数:

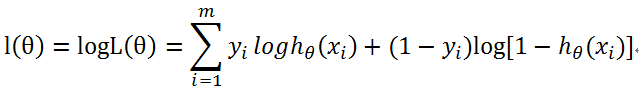
目标是求得损失函数的最大值，即：最大似然估计。要得到损失函数的最大值，可转化为求其最小值

其最小值是：

即：

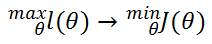
使用梯度下降法，求J的最小值。

由于：

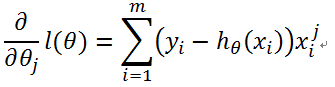
因此：

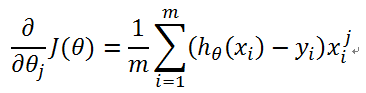
更新过程：

---

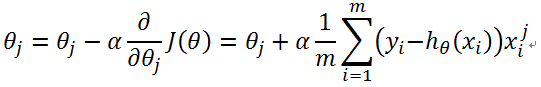
如有错误之处，请评论中指正。