[洛谷P4491] [HAOI2018]染色

洛谷题目链接:[HAOI2018]染色

题目背景

HAOI2018 Round2 第二题

题目描述

为了报答小 C 的苹果, 小 G 打算送给热爱美术的小 C 一块画布, 这块画布可 以抽象为一个长度为 \(N\) 的序列, 每个位置都可以被染成 \(M\) 种颜色中的某一种.

然而小 C 只关心序列的 \(N\) 个位置中出现次数恰好为 \(S\) 的颜色种数, 如果恰 好出现了 \(S\) 次的颜色有 \(K\) 种, 则小 C 会产生 \(W_k\) 的愉悦度.

小 C 希望知道对于所有可能的染色方案, 他能获得的愉悦度的和对 \(1004535809\) 取模的结果是多少.

输入输出格式

输入格式：

从标准输入读入数据. 第一行三个整数 \(N, M, S\).

接下来一行 \(M + 1\) 个整数, 第 \(i\) 个数表示 \(W_{i-1}\)​ .

输出格式：

输出到标准输出中. 输出一个整数表示答案．

输入输出样例

输入样例#1：

8 8 3

3999 8477 9694 8454 3308 8961 3018 2255 4910

输出样例#1：

524070430

输入样例#2：

见 https://www.luogu.org/paste/rxrv9utg

输出样例#2：

231524284

说明

特殊性质: \(\forall 1 \le i \le m, W_i = 0\)

对于 \(100\%\) 的数据, 满足 \(0 \le W_i < 1004535809\)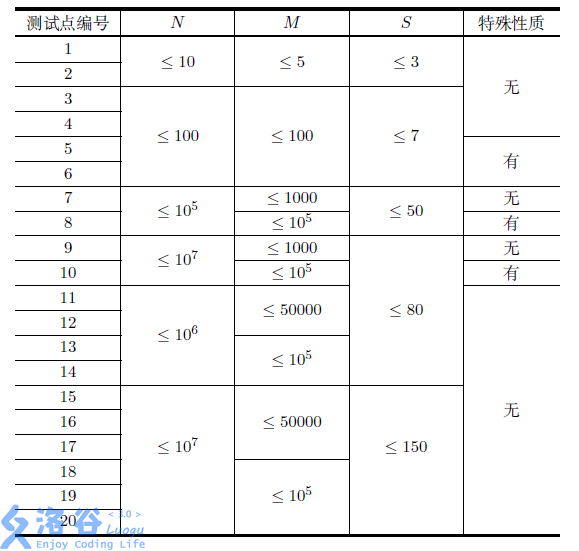

题解: 设\(f[i]\)表示出现次数恰好等于\(S\)的颜色个数大于等于\(i\)的方案数,从\(m\)种颜色中选出\(i\)种颜色的方案是\(C_m^i\),将染色的序列看做一个有可重元素的排列,那么方案数就是$$f[i]=C_m^{i*\frac{n!}{(n-S*i)!(S!)}i}(n-Si)^{m-i}$$

之所以是大于等于,是因为式子的最后面那部分还可能有出现次数恰好等于\(S\)的颜色.

设\(lim=min(\lfloor\frac{n}{s} \rfloor,m)\).

设\(ans[i]\)表示出现次数恰好等于\(S\)的颜色个数恰好等于\(i\)的方案数,根据容斥,有:$$ans[i]=\sum_{j=i}^{lim}(-1){j-i}C_j^if[j]$$

将式子中的组合数拆开$$ans[i]i!=\sum_{j=i}^{{lim}*\frac{(-1)}{j-i}}{(j-i)!}\frac{f[j]}{j!}$$

可以发现这是一个卷积的形式,设\(A[i]=\frac{(-1)^{i}}{i!},B[i]=\frac{f[i]}{i}\),那么将\(A\)的系数翻转,再与\(B\)做多项式乘法就可以了.

最后在统计答案的时候要注意,因为将\(A\)的系数翻转了,所以求出来的结果相当于是\(C_{i+lim}=A^{'}_{lim+i-j}*B_j\),所以在统计出现\(i\)次的方案数时要将数组的下标加\(lim\).

#include<bits/stdc++.h>
using namespace std;
const int N = 1e7+5;
const int M = 3e5+5;
const int mod = 1004535809;

int n, m, s, lim, r[M], len = 0, f[M], ans = 0, w[N], a[N], cnt[N];
int pinv[N], inv[N], fac[N];

void init(int n){
    pinv[0] = inv[0] = fac[0] = pinv[1] = inv[1] = fac[1] = 1;
    for(int i = 2; i <= n; i++){
        fac[i] = 1ll*fac[i-1]*i%mod;
        inv[i] = 1ll*(mod-mod/i)*inv[mod%i]%mod;
        pinv[i] = 1ll*pinv[i-1]*inv[i]%mod;
    }
}

int C(int n, int m){ return 1ll*fac[n]*pinv[m]%mod*pinv[n-m]%mod; }

int qpow(int x, int n){
    int res = 1;
    for(; n; x = 1ll*x*x%mod, n >>= 1)
        if(n & 1) res = 1ll*res*x%mod;
    return res;
}

void NTT(int *A, int f){
    for(int i = 0; i < n; i++) if(i < r[i]) swap(A[i], A[r[i]]);
    for(int i = 1; i < n; i <<= 1){
        int wi = qpow(3, (mod-1)/(i << 1)), x, y;
        if(f == -1) wi = qpow(wi, mod-2);
        for(int j = 0; j < n; j += (i << 1)){
            for(int k = 0, w = 1; k < i; k++, w = 1ll*w*wi%mod){
                x = A[j+k], y = 1ll*A[i+j+k]*w%mod;
                A[j+k] = (x+y)%mod, A[i+j+k] = (x-y+mod)%mod;
            }
        }
    }
    if(f == -1){
        int invn = qpow(n, mod-2);
        for(int i = 0; i < n; i++) A[i] = 1ll*A[i]*invn%mod;
    }
}

int main(){
    ios::sync_with_stdio(false);
    cin >> n >> m >> s, lim = min(m, n/s), init(max(n, m));
    for(int i = 0; i <= m; i++) cin >> w[i];
    for(int i = 0; i <= lim; i++)
        cnt[i] = 1ll*fac[n]*qpow(pinv[s], i)%mod*pinv[n-s*i]%mod*C(m, i)%mod*qpow(m-i, n-s*i)%mod*fac[i]%mod;
    for(int i = 0; i <= lim; i++) a[i] = (((lim-i)&1) ? (mod-pinv[lim-i]) : pinv[lim-i]);
    for(n = 1; n < (lim+1 << 1); n <<= 1) len++;
    for(int i = 0; i < n; i++) r[i] = (r[i>>1]>>1)|((i&1)<<len-1);
    NTT(cnt, 1), NTT(a, 1);
    for(int i = 0; i < n; i++) cnt[i] = 1ll*cnt[i]*a[i]%mod;
    NTT(cnt, -1);
    for(int i = 0; i <= lim; i++) (ans += 1ll*cnt[lim+i]*pinv[i]%mod*w[i]%mod) %= mod;
    cout << ans << endl;
    return 0;
}