codeforces997C Sky full of stars

传送门：http://codeforces.com/problemset/problem/997/C

【题解】

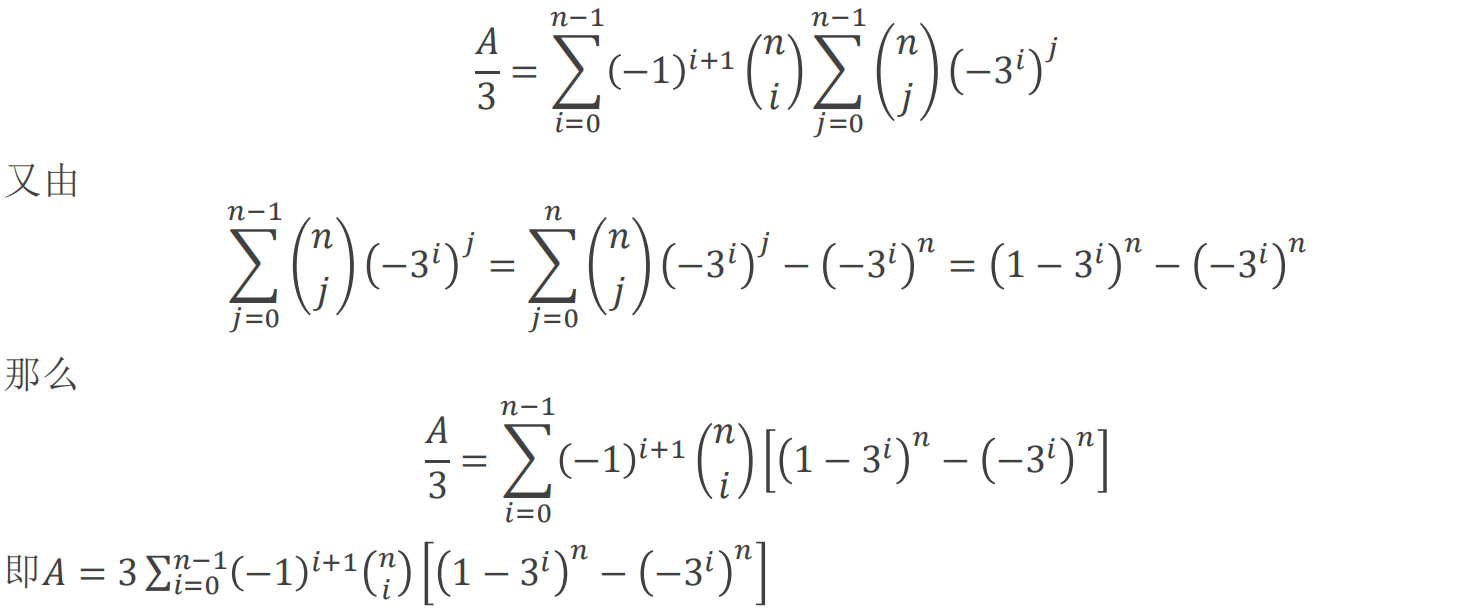
注意在把$i=0$或$j=0$分开考虑的时候，3上面的指数应该是$n(n-j)+j$

至少一行一列相同颜色，那么这些相同颜色的行列一定是同一种颜色，所以是$3^((n-i)(n-j)+1)$。

如果只有若干行相同颜色，那么这些相同颜色的行之间的颜色不一定相同，所以是$3^((n-j)j+j)$。

# include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int mod = ;
const int M = 1e6 + ;

int n, fac[M], inv[M];

inline int pwr(int a, int b) {
    int ret = ;
    while(b) {
        if(b&) ret = 1ll * ret * a % mod;
        a = 1ll * a * a % mod;
        b >>= ;
    }
    return ret;
}

inline int C(int n, int m) {
    return 1ll * fac[n] * inv[m] % mod * inv[n-m] % mod;
}

int main() {
    cin >> n;
    fac[] = ; inv[] = ;
    for (int i=; i<=n; ++i) fac[i] = 1ll * fac[i-] * i % mod;
    inv[n] = pwr(fac[n], mod-);
    for (int i=n-; i>=; --i) inv[i] = 1ll * inv[i+] * (i+) % mod;
    int A = , B = ;
    for (int j=; j<=n; ++j) {
        int tem = 1ll * C(n, j) * pwr(, (1ll * n * (n-j) + j) % (mod-)) % mod;
        if(j&) B += tem;
        else B -= tem;
        if(B >= mod) B -= mod;
        if(B < ) B += mod;
    }
    B <<= ;
    if(B >= mod) B -= mod; 

    int q = ;
    for (int i=; i<n; ++i) {
        int t = pwr(-q+mod+, n) - pwr(-q+mod, n);
        if(t < ) t += mod;
        if(i&) A = A + 1ll * C(n, i) * t % mod;
        else A = A - 1ll * C(n, i) * t % mod;
        if(A >= mod) A -= mod;
        if(A < ) A += mod;
        q = 3ll * q % mod;
    }
    A = 3ll * A % mod;
    int ans = A+B;
    if(ans >= mod) ans -= mod;
    cout << ans;

    return ;
}