梯度下降法的三种形式-BGD、SGD、MBGD

在应用机器学习算法时，我们通常采用梯度下降法来对采用的算法进行训练。其实，常用的梯度下降法还具体包含有三种不同的形式，它们也各自有着不同的优缺点。

下面我们以线性回归算法来对三种梯度下降法进行比较。

一般线性回归函数的假设函数为：

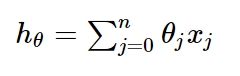
对应的损失函数为：

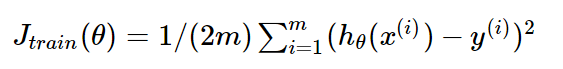
下图为一个二维参数（θ0和θ1）组对应能量函数的可视化图：

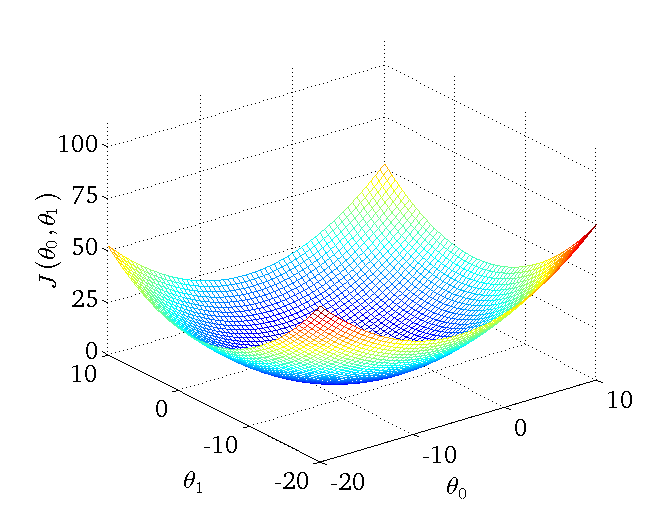
1、批量梯度下降法BGD

批量梯度下降法（Batch Gradient Descent，简称BGD）是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新。

我们的目的是要误差函数尽可能的小，即求解weights使误差函数尽可能小。首先，我们随机初始化weigths，然后不断反复的更新weights使得误差函数减小，直到满足要求时停止。这里更新算法我们选择梯度下降算法，利用初始化的weights并且反复更新weights：

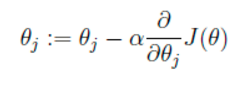
这里代表学习率，表示每次向着J最陡峭的方向迈步的大小。为了更新weights，我们需要求出函数J的偏导数。首先当我们只有一个数据点（x,y）的时候，J的偏导数是：

                                   

则对所有数据点，上述损失函数的偏导（累和）为：

再最小化损失函数的过程中，需要不断反复的更新weights使得误差函数减小，更新过程如下：

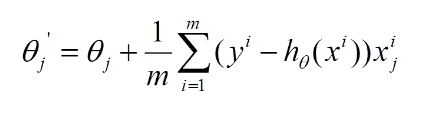
那么好了，每次参数更新的伪代码如下：

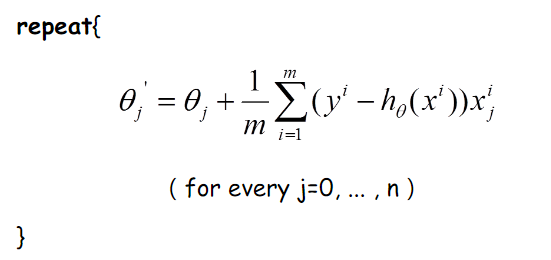
由上图更新公式我们就可以看到，我们每一次的参数更新都用到了所有的训练数据（比如有m个，就用到了m个），如果训练数据非常多的话，是非常耗时的。

下面给出批梯度下降的收敛图：

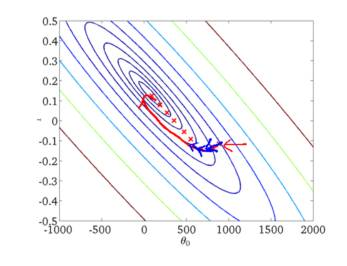
从图中，我们可以得到BGD迭代的次数相对较少。

代码实现：

def batchGradientDescent(x, y, theta, alpha, m, maxIteration):
    for i in range(maxIteration):
        hypothesis = np.dot(x, theta)
        loss = hypothesis - y
        gradient = np.dot(x.transpose(), loss) / m
        theta = theta - alpha * gradient              # 对所有样本求和
    return theta

2、随机梯度下降法SGD

由于批梯度下降每跟新一个参数的时候，要用到所有的样本数，所以训练速度会随着样本数量的增加而变得非常缓慢。随机梯度下降正是为了解决这个办法而提出的。它是利用每个样本的损失函数对θ求偏导得到对应的梯度，来更新θ：

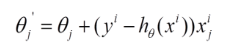
更新过程如下：

随机梯度下降是通过每个样本来迭代更新一次，对比上面的批量梯度下降，迭代一次需要用到所有训练样本（往往如今真实问题训练数据都是非常巨大），一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。

但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

随机梯度下降收敛图如下：

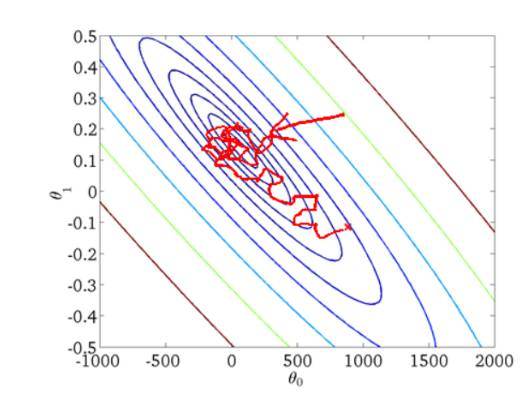
我们可以从图中看出SGD迭代的次数较多，在解空间的搜索过程看起来很盲目。但是大体上是往着最优值方向移动。

代码实现：

def StochasticGradientDescent(x, y, theta, alpha, m, maxIteration):
    data = []
    for i in range(10):
        data.append(i)
    # 这里随便挑选一个进行更新点进行即可（不用想BGD一样全部考虑）

    for i in range(maxIteration):
        hypothesis = np.dot(x, theta)
        loss = hypothesis - y  # 这里还是有十个样本
        index = random.sample(data, 1)[0]  # 随机抽取一个样本，得到它的下标
        gradient = loss[index] * x[index]  # 只取一个点进行更新计算
        theta = theta - alpha * gradient.T
    return theta

3、min-batch 小批量梯度下降法MBGD

我们从上面两种梯度下降法可以看出，其各自均有优缺点，那么能不能在两种方法的性能之间取得一个折衷呢？既算法的训练过程比较快，而且也要保证最终参数训练的准确率，而这正是小批量梯度下降法（Mini-batch Gradient Descent，简称MBGD）的初衷。

我们假设每次更新参数的时候用到的样本数为10个（不同的任务完全不同，这里举一个例子而已）

更新伪代码如下：

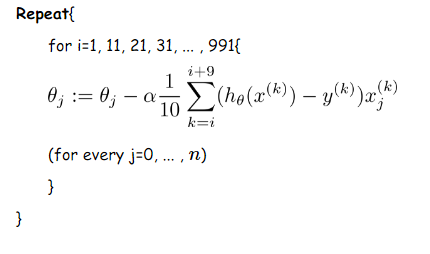
4、三种梯度下降方法的总结

1.批梯度下降每次更新使用了所有的训练数据，最小化损失函数，如果只有一个极小值，那么批梯度下降是考虑了训练集所有数据，是朝着最小值迭代运动的，但是缺点是如果样本值很大的话，更新速度会很慢。

2.随机梯度下降在每次更新的时候，只考虑了一个样本点，这样会大大加快训练数据，也恰好是批梯度下降的缺点，但是有可能由于训练数据的噪声点较多，那么每一次利用噪声点进行更新的过程中，就不一定是朝着极小值方向更新，但是由于更新多轮，整体方向还是大致朝着极小值方向更新，又提高了速度。

3.小批量梯度下降法是为了解决批梯度下降法的训练速度慢，以及随机梯度下降法的准确性综合而来，但是这里注意，不同问题的batch是不一样的。