R语言-上海二手房数据分析

案例:通过分析上海的二手房的数据,分析出性价比(地段,价格,未来的升值空间)来判断哪个区位的二手房性价比最高

1.载入包

library(ggplot2)
library(Hmisc)
library(car)
library(caret)

2.加载数据集

houses <- read.csv('E:\\Udacity\\Data Analysis High\\R\\R_Study\\二手房分析案例\\链家二手房.csv',sep=',',header=T)

3.查看数据集

describe(houses)

数据集有以下几个字段构成

## 小区名称
## 户型
## 面积
## 区域
## 楼层
## 朝向
## 价格.W.
## 单价.平方米.
## 建筑时间

探究影响房价的主要因素是什么

4.查看户型的分布

type_freq <- data.frame(table(houses$户型))
type_p <- ggplot(data=type_freq,aes(x=reorder(Var1,-Freq),y=Freq))+
  geom_bar(stat='identity',fill='steelblue')+
  theme(axis.text.x = element_text(angle = 30,vjust = 0.5))+
  xlab('户型')+
  ylab('套数')
type_p

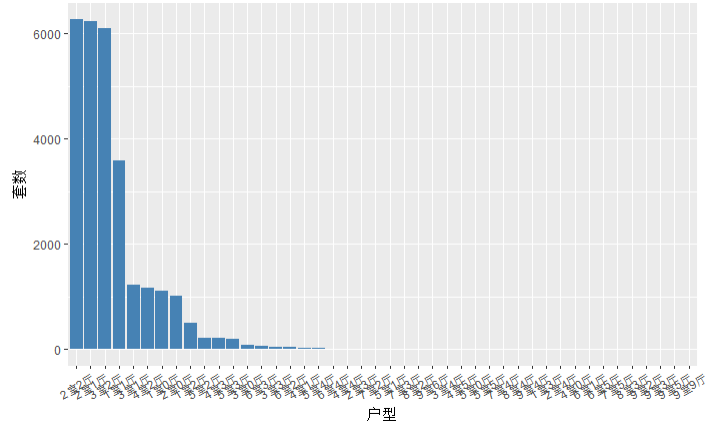
　　结论:户型的分布不符合正态分布

　　　　 需要对户型的数据进行清洗,找出主要的户型

5.对户型数据进行清洗

# 把低于一千套的房型设置为其他
type <- c('2室2厅','2室1厅','3室2厅','1室1厅','3室1厅','4室2厅','1室0厅','2室0厅','4室1厅')

houses$type.new <- ifelse(houses$户型 %in% type,as.character(houses$户型),'其他')
type_freq <- data.frame(table(houses$type.new))
# 绘图
type_p <- ggplot(data = type_freq, mapping = aes(x = reorder(Var1, -Freq),y = Freq)) +
  geom_bar(stat = 'identity', fill = 'steelblue') +
  theme(axis.text.x  = element_text(angle = 30, vjust = 0.5)) +
  xlab('户型') + ylab('套数')
type_p

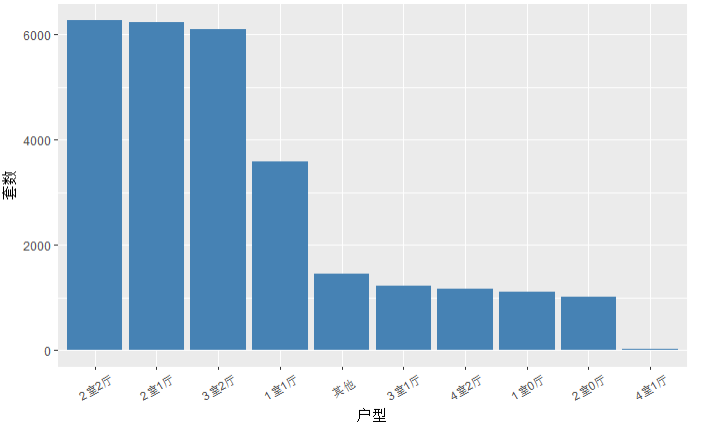
　　结论:2室2厅,2室1厅,3室2厅是上海比较多的二手房户型

6.楼层数据清洗

# 新建floor变量,使用ifelse来判断具体的楼层
houses$floor <- ifelse(substring(houses$楼层,1,2) %in% c('低区','高区','中区'),substring(houses$楼层,1,2),'低区')
# 计算百分比
percent <- paste(round(prop.table(table(houses$floor))*100,2),'%',sep = '')
df <- data.frame(table(houses$floor))
df <- cbind(df,percent)
df

7.建筑时间清洗

# 自定义众数函数
stat.mode <- function(x, rm.na = TRUE){
  if (rm.na == TRUE){
    y = x[!is.na(x)]
  }
  res = names(table(y))[which.max(table(y))]
  return(res)
}
# 自定义函数，实现分组替补
my.impute <- function(data, category.col = NULL,
                      miss.col = NULL, method = stat.mode){
  impute.data = NULL
  for(i in as.character(unique(data[,category.col]))){
    sub.data = subset(data, data[,category.col] == i)
    sub.data[,miss.col] = impute(sub.data[,miss.col], method)
    impute.data = c(impute.data, sub.data[,miss.col])
  }
  data[,miss.col] = impute.data
  return(data)
}
# 将建筑时间中空白字符串转换为缺失值
houses$建筑时间[houses$建筑时间 == ''] <- NA
#分组替补缺失值，并对数据集进行变量筛选

final_house <- subset(my.impute(houses, '区域', '建筑时间'),select = c(type.new,floor,面积,价格.W.,单价.平方米.,建筑时间))
#构建新字段builtdate2now，即建筑时间与当前2016年的时长
final_house <- transform(final_house, builtdate2now = 2016-as.integer(substring(as.character(建筑时间),1,4)))
#删除原始的建筑时间这一字段
final_house <- subset(final_house, select = -建筑时间)

8.查看房价和面积的正态分布

# 自定义正态分布的函数
# 自定义绘图函数
norm.test <- function(x, breaks = 20, alpha = 0.05,
plot = TRUE){
if(plot == TRUE)
{#设置图形界面（多图合为一张图）
opar <- par(no.readonly = TRUE)
layout(matrix(c(1,1,2,3),2,2,byrow = TRUE),
width = c(2,2),heights = c(2,2))
#绘制直方图
hist(x, freq = FALSE, breaks = seq(min(x),
max(x), length = breaks), main = 'x的直方图',
ylab = '核密度值')
#添加核密度图
lines(density(x), col = 'red', lty = 1, lwd = 2)
#添加正态分布图
x <- x[order(x)]
lines(x, dnorm(x, mean(x), sd(x)),
col = 'blue', lty = 2, lwd = 2.5)
#添加图例
legend('topright',
legend = c('核密度曲线','正态分布曲线'),
col = c('red','blue'), lty = c(1,2),
lwd = c(2,2.5), bty = 'n')
#绘制Q-Q图
qqnorm(x, xlab = '实际分布', ylab = '正态分布',
main = 'x的Q-Q图', col = 'blue')
qqline(x)
#绘制P-P图
P <- pnorm(x, mean(x), sd(x))
cdf <- 0
for(i in 1:length(x)){cdf[i] <- sum(x <= x[i])/length(x)}
plot(cdf, P, xlab = '实际分布', ylab = '正态分布',
main = 'x的P-P图', xlim = c(0,1),
ylim = c(0,1), col = 'blue')
abline(a = 0, b = 1)
par(opar)
}
#定量的shapiro检验
if (length(x) <= 5000) {
shapiro <- shapiro.test(x)
if(shapiro$p.value > alpha)
print(paste('定量结果为：', 'x服从正态分布，',
'P值 =',round(shapiro$p.value,5), '> 0.05'))
else
print(paste('定量结果为：', 'x不服从正态分布，',
'P值 =',round(shapiro$p.value,5), '<= 0.05'))
shapiro
}
else {
ks <- ks.test(x,'pnorm')
if(ks$p.value > alpha)
print(paste('定量结果为：', 'x服从正态分布，',
'P值 =',round(ks$p.value,5), '> 0.05'))
else
print(paste('定量结果为：', 'x不服从正态分布，',
'P值 =',round(ks$p.value,5), '<= 0.05'))
ks
}
}

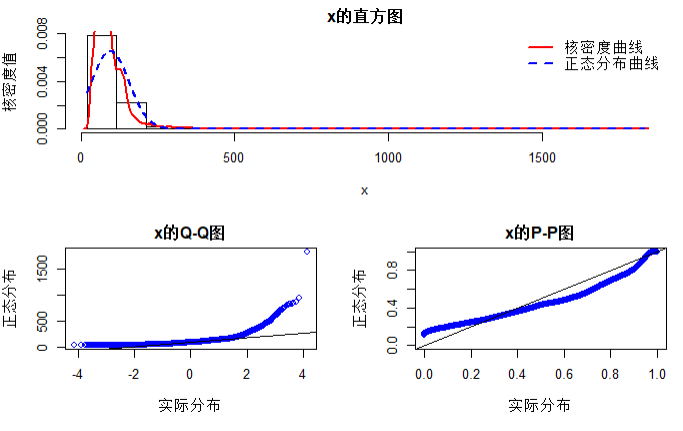
# 面积的正态检验
norm.test(houses$面积)

# 价格的正态检验
norm.test(houses$价格.W.)

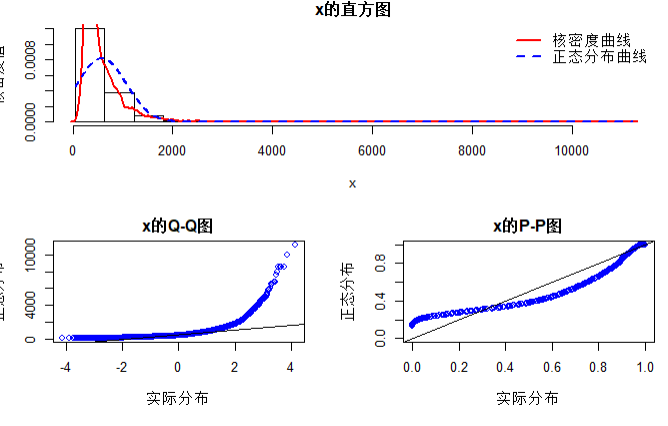
　　结论:房价和面积均不服从正态分布,因此不能对其进行做线性回归模型

9.查看上海地区二手房的均价

avg_price <- aggregate(houses$单价.平方米.,by=list(houses$区域),FUN=mean)
p <- ggplot(data=avg_price,aes(x=reorder(Group.1,-x),y=x,group=1))+
  geom_area(fill='lightgreen')+
  geom_line(colour = 'steelblue', size = 2)+
  geom_point()+
  ylab('均价')
p

　　　　 　　结论:静安区和徐汇区的价格较高

10.模型构建

　　在对房屋进行建模的时候,首先使用聚类把不同类型的房子给划分出来,我选择面积,房价,单价/㎡来进行聚类的划分

　　10.1 聚类的个数

# 模型构建
tot.wssplot <- function(data,nc,seed=1234){
# 计算距离的平方和
  tot.wss <- (nrow(data)-1) * sum(apply(data,2,var))
  for(i in 2:nc){
    set.seed(seed)
    tot.wss[i] <- kmeans(data,centers = i,iter.max = 100)$tot.withinss
  }
  plot(1:nc,tot.wss,type='b',xlab = 'Number of Cluster',
       ylab = 'Within groups sum of squares',col='blue',lwd=2,
       main='choose best clusters')
}
# 找出判断聚类的三个主要的指标
stander <- data.frame(scale(final_house[,c('面积','价格.W.','单价.平方米.')]))
# 做出聚类个数图
tot.wssplot(stander,15)

　　结论:分成5个类的模型的效果会比较好

　　10.2聚类

set.seed(1234)
clust <- kmeans(x=stander,centers = 5,iter.max = 100)
table(clust$cluster)

　　结论:每个聚类的结果

　10.3查看聚类的结果

# 查看每个户型的平均面积
aggregate(final_house$面积,list(final_house$type.new),FUN=mean)

# 比较每个类中的面积,单价,每平米价格
aggregate(final_house[,3:5],list(clust$cluster),FUN=mean)

　　结论:

　　　　第1组是地段型的房子,地段位于上海的核心区域,每平米的单价是最高的

　　　　第2组是面积型的房子,地段稍逊于第1组,面积都在350平米以上,属于享受阶层买得起的房子

　　　　第3组是均衡型的房子,地段和面积均属于发展中的状态,房价涨势稳定,将来的发展空间较大

　　　　第4组是廉价型的房子,面积和价格都相对比较低,地段和面积相对较低

　　10.4聚类的散点图

p <- ggplot(data=final_house[,3:5],aes(x=面积,y=单价.平方米.,color=factor(clust$cluster)))+
  geom_point(pch=20,size=3)+
  scale_color_manual(values = c('red','blue','green','black','orange'))
p

11建模

　　11.1 将类别变量变成因子类型

final_house$floor <- factor(final_house$floor)
final_house$type.new <- factor(final_house$type.new)
final_house$clsuter <- factor(clust$cluster)

　　11.2构建公式

# 选择出所有的因子变量
factors <- names(final_house)[sapply(final_house, class)=='factor']
formal <- f <- as.formula(paste('~',paste(factors,collapse = '+')))
dummy <- dummyVars(formula = formal,data=final_house)
pred <- predict(dummy,newdata=final_house)
head(pred)

　　11.3建模

final_house2 <- cbind(final_house,pred)
# 选择需要建模的因子
model_data <- subset(final_house2,select=-c(1,2,3,8,17,18,24))
fit1 <- lm(价格.W. ~ .,data=model_data)
summary(fit1)

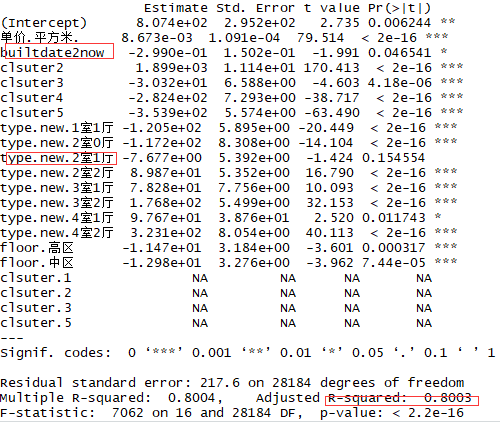
　　结论:建造时间和2室1厅的影响不明显,需要对模型进行修改

　　11.4修改模型

#由于房价不符合正态分布,所以要对价格取对数
powerTransform(fit1)
fit2 <- lm(log(价格.W.) ~ .,data=model_data)
summary(fit2)

　　结论:R²的值得到了提高,并且建造时间和2室1厅的影响已经计入到模型中去

　　11.5查看最终模型的诊断结果

opar <- par(no.readonly = TRUE)
par(mfrow = c(2,2))
plot(fit2)
par(opar)

　　结论:符合线性回归模型的假设