POJ1390 Blocks 【动态规划】

Blocks

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 4173		Accepted: 1661

Description

Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold. 
The corresponding picture will be as shown below: 
 
Figure 1

If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1
box(es) in the segments respectively. 

Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points. 

Now let's look at the picture below: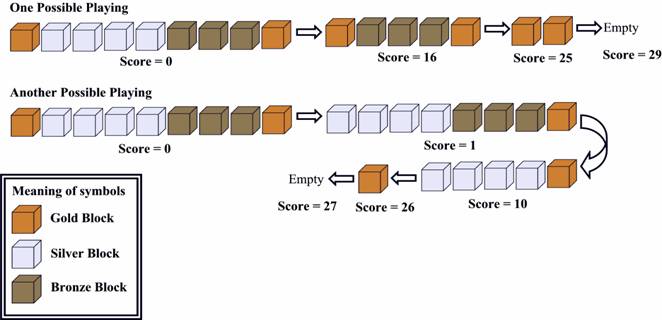 
 
Figure 2

The first one is OPTIMAL. 

Find the highest score you can get, given an initial state of this game. 

Input

The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range
1~n.

Output

For each test case, print the case number and the highest possible score.

Sample Input

2
9
1 2 2 2 2 3 3 3 1
1
1

Sample Output

Case 1: 29
Case 2: 1

题意：给定n个方块，当中有些颜色是连续的，每次点击一个方块就能够消除掉跟它连续的同样的颜色的方块，获得积分为消除长度的平方。给定一个方块序列，求最大能获得多少积分。

题解：状态方程score[i][j][k]为将连续小块统计成大块后从第i个到第j个慷慨块且第j个后面有k个连续的与其同色的方块所获得的最大积分。

我认为有问题的代码。仿照着讲义代码写的。可是也能AC。并且时间消耗是344ms。 应该是那个地方我没理解：

#include <stdio.h>
#include <string.h>
#define maxn 200

struct Node{
    int color, len;
} segment[maxn];
int score[maxn][maxn][maxn], arr[maxn];

int clickBox(int left, int right, int exLen)
{
    if(score[left][right][exLen]) return score[left][right][exLen];
    int i, ans, ans2;
    ans = segment[right].len + exLen;
    ans = ans * ans;
    if(left == right) return score[left][right][exLen] = ans;
    ans += clickBox(left, right - 1, 0);
    for(i = right - 1; i >= left; --i){
        if(segment[i].color != segment[right].color) continue;
        ans2 = clickBox(left, i, exLen + segment[right].len) +
                clickBox(i + 1, right - 1, 0);
        if(ans2 <= ans) continue;
        ans = ans2; break;
    }
    return score[left][right][exLen] = ans;
}

int main()
{
    int t, n, i, id, cas = 1;
    scanf("%d", &t);
    while(t--){
        scanf("%d", &n);
        for(i = 0; i < n; ++i) scanf("%d", arr + i);
        memset(score, 0, sizeof(score));
        segment[id = 0].color = arr[0];
        segment[id].len = 1;
        for(i = 1; i < n; ++i){
            if(arr[i] != arr[i-1]){
                segment[++id].color = arr[i];
                segment[id].len = 1;
            }else ++segment[id].len;
        }
        printf("Case %d: %d\n", cas++, clickBox(0, id, 0));
    }
    return 0;
}

我认为没问题的代码，时间消耗1688ms：

#include <stdio.h>
#include <string.h>
#define maxn 200

struct Node{
    int color, len;
} segment[maxn];
int score[maxn][maxn][maxn], arr[maxn];

int clickBox(int left, int right, int exLen)
{
    if(score[left][right][exLen]) return score[left][right][exLen];
    int i, ans, ans2;
    ans = segment[right].len + exLen;
    ans = ans * ans;
    if(left == right) return score[left][right][exLen] = ans;
    ans += clickBox(left, right - 1, 0);
    for(i = right - 1; i >= left; --i){
        if(segment[i].color != segment[right].color) continue;
        ans2 = clickBox(left, i, exLen + segment[right].len) +
                clickBox(i + 1, right - 1, 0);
        if(ans2 > ans) ans = ans2;
    }
    return score[left][right][exLen] = ans;
}

int main()
{
    int t, n, i, id, cas = 1;
    scanf("%d", &t);
    while(t--){
        scanf("%d", &n);
        for(i = 0; i < n; ++i) scanf("%d", arr + i);
        memset(score, 0, sizeof(score));
        segment[id = 0].color = arr[0];
        segment[id].len = 1;
        for(i = 1; i < n; ++i){
            if(arr[i] != arr[i-1]){
                segment[++id].color = arr[i];
                segment[id].len = 1;
            }else ++segment[id].len;
        }
        printf("Case %d: %d\n", cas++, clickBox(0, id, 0));
    }
    return 0;
}