[NOIP2016day2T1] 組合數問題(problem)

题目描述

组合数C(n,m)表示的是从n个物品中选出m个物品的方案数。举个例子，从（1,2,3) 三个物品中选择两个物品可以有（1,2),(1,3),(2,3)这三种选择方法。根据组合数的定义，我们可以给出计算组合数的一般公式：

C(n,m)=n!/m!(n-m)!

其中n! = 1 × 2 × · · · × n

小葱想知道如果给定n,m和k，对于所有的0 <= i <= n，0 <= j <= min(i,m)有多少对 (i,j)满足C(i,j)是k的倍数。

输入输出格式

输入格式：

第一行有两个整数t,k，其中t代表该测试点总共有多少组测试数据，k的意义见【问题描述】。

接下来t行每行两个整数n,m，其中n,m的意义见【问题描述】。

输出格式：

t行，每行一个整数代表答案。

输入输出样例

输入样例#1：

1 2

3 3

输出样例#1：

输入样例#2：

输出样例#2：

0

7

说明

【样例1说明】

在所有可能的情况中，只有C(2,1)=2是2的倍数。

【子任务】

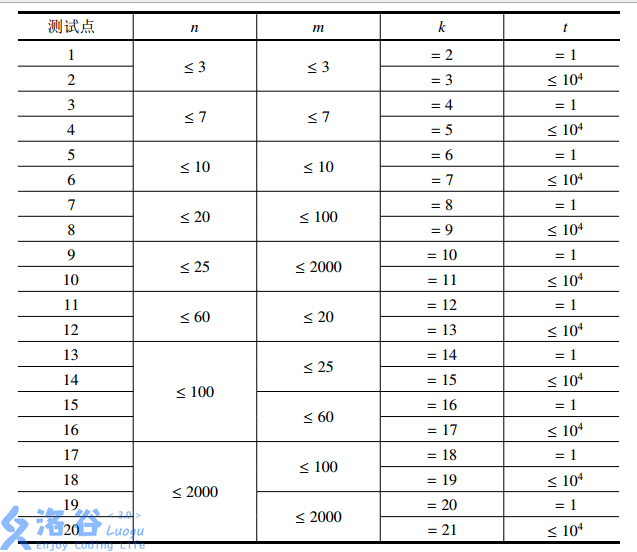
這個題，首先暴力思路是質因數分解。（70分）

 #include<cstdio>

 int t,k,n,m,ans,pd,a;

 int s[]={,,,,,,,};

 int bz[],bd[];

 int main(){

     freopen("problem.in","r",stdin);

     freopen("problem.ans","w",stdout);

     scanf("%d%d",&t,&k);

     for(int i=;i<&&k>=s[i];i++) while(k%s[i]==){k/=s[i];bz[i]++;}

     while(t--){

         ans=;

         scanf("%d%d",&n,&m);

         for(int i=;i<=n;i++)

         for(int j=;j<=i&&j<=m;j++){

             pd=;

             for(int k=j+;k<=i;k++){

                 a=k;

                 for(int l=;l<&&a>=s[l];l++) while(a%s[l]==){a/=s[l];bd[l]++;}

             }

             for(int k=;k<=i-j;k++){

                 a=k;

                 for(int l=;l<&&a>=s[l];l++) while(a%s[l]==){a/=s[l];bd[l]--;}

             }

             for(int k=;k<;k++){

                 if(bd[k]<bz[k]) pd=;

                 bd[k]=;

             }

             ans+=pd;

         }

         printf("%d\n",ans);

     }

 }

暴力

然後，組合數有一個遞推公式，即C(i,j)=C(i-1,j)+C(i-1,j-1)，也就是大名鼎鼎的楊輝三角。

 #include<cstdio>

 int t,k,n,m,ans;

 int c[][];

 int main(){

     freopen("problem.in","r",stdin);

     freopen("problem.ans","w",stdout);

     scanf("%d%d",&t,&k);

     c[][]=c[][]=;

     for(int i=;i<=;i++)

     for(int j=;j<=i;j++){

         c[i][j]=c[i-][j]+c[i-][j-];

         c[i][j]%=k;

     }

     while(t--){

         ans=;

         scanf("%d%d",&n,&m);

         for(int i=;i<=n;i++)

         for(int j=;j<=i&&j<=m;j++)

         if(!c[i][j]) ++ans;

         printf("%d\n",ans);

     }

     return ;

 }

90分

而後提前處理一下，把查詢變成O(1)。

 1 #include<cstdio>

 2 int t,k,n,m,a;

 3 int c[2010][2010];

 4 int ans[2010][2010];

 5 int main(){

 6     freopen("problem.in","r",stdin);

 7     freopen("problem.ans","w",stdout);

 8     scanf("%d%d",&t,&k);

 9     c[1][0]=c[1][1]=1;

10     for(int i=2;i<=2000;i++)

11     for(int j=0;j<=i;j++){

12         c[i][j]=c[i-1][j]+c[i-1][j-1];

13         c[i][j]%=k;

14     }

15     for(int i=1;i<=2000;i++){

16         a=0;

17         for(int j=0;j<i;j++){

18             if(!c[i][j]) ++a;

19             ans[i][j]=ans[i-1][j]+a;

20         }

21         for(int j=i;j<=2000;j++) ans[i][j]=ans[i][i-1];

22     }

23     while(t--){

24         scanf("%d%d",&n,&m);

25         printf("%d\n",ans[n][m]);

26     }

27     return 0;

28 }

NOIP第二水的題，而後。。。