一、什么是PCA

主成分分析 Principal Component Analysis

一个非监督学的学习算法

主要用于数据的降维

通过降维，可以发现更便于人类理解的特征

其他应用：可视化；去噪

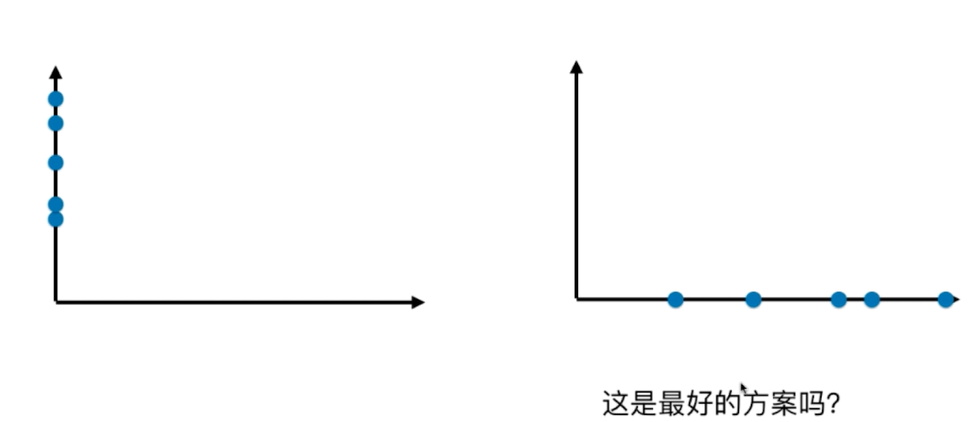
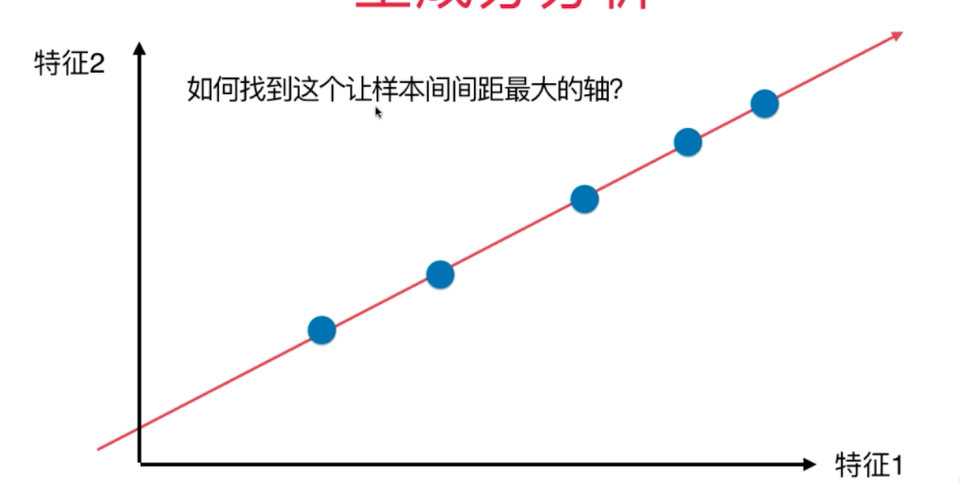
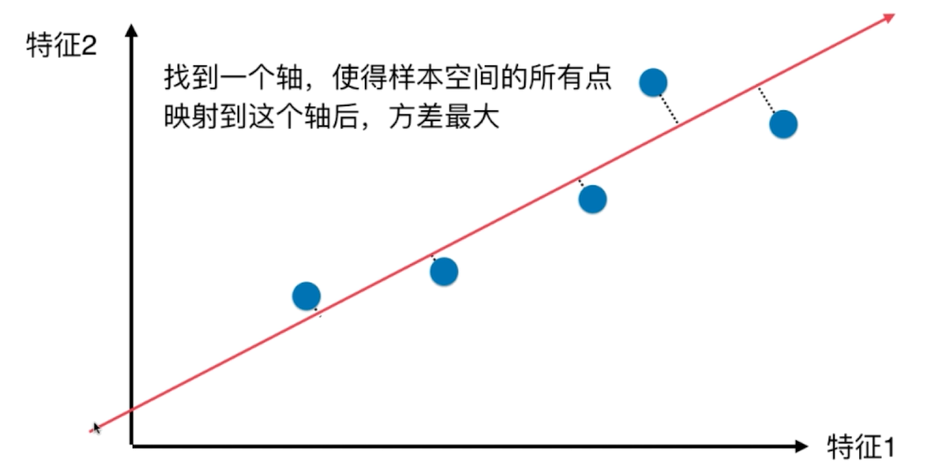
第一步：将样例的均值归零（demean）

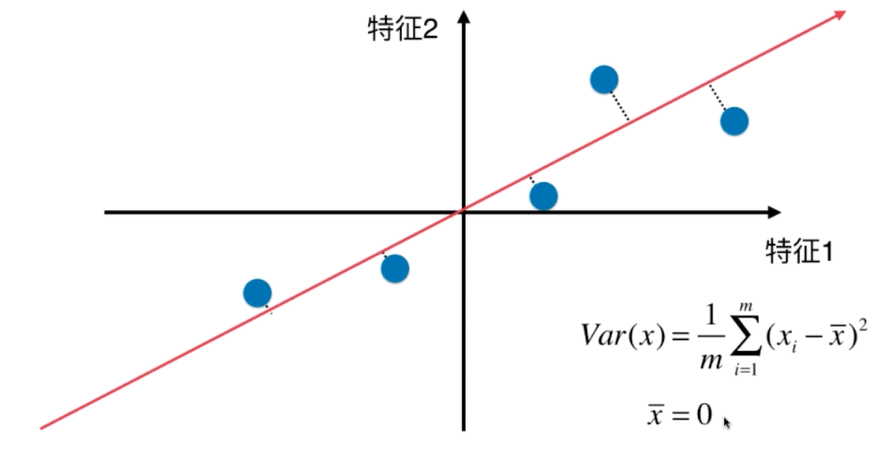
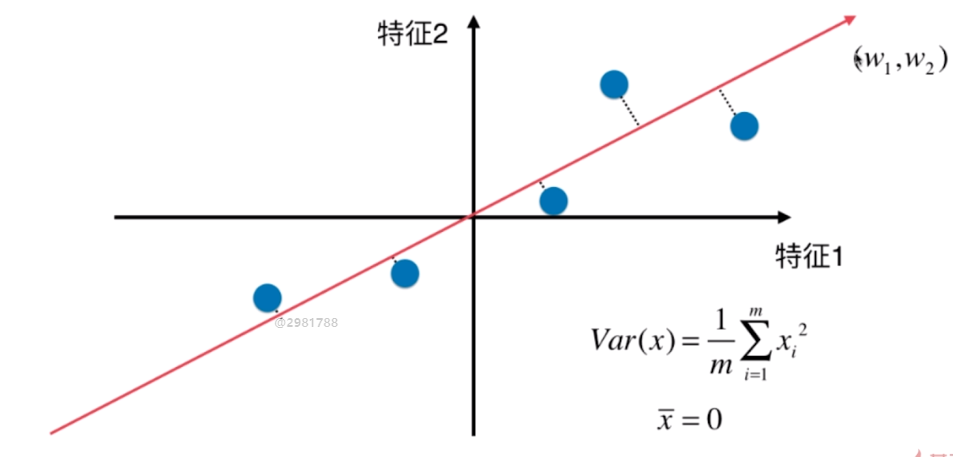
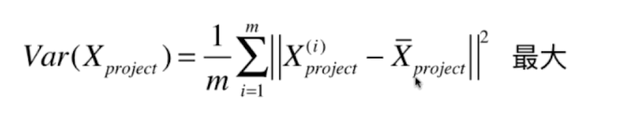
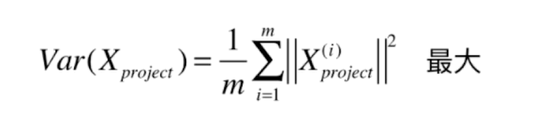
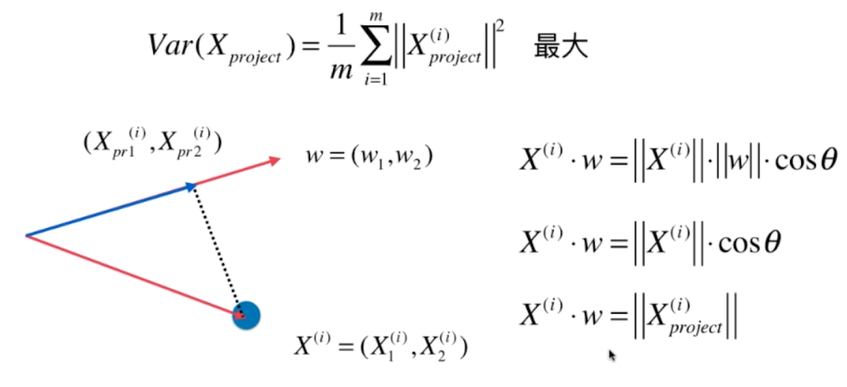
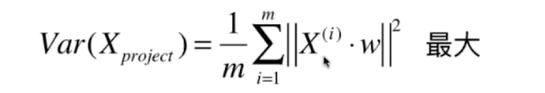
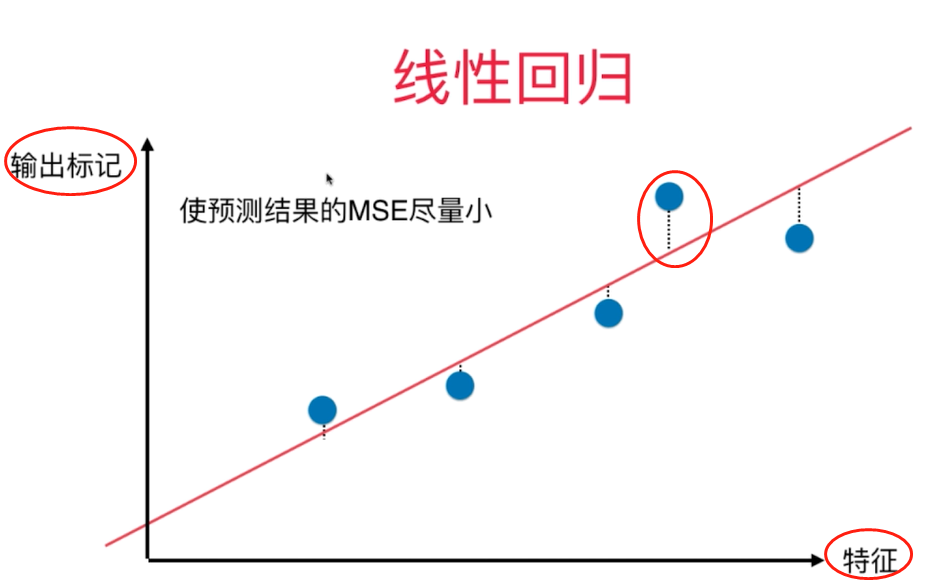
二、使用梯度上升法求解PCA问题

梯度上升法解决主成分分析问题

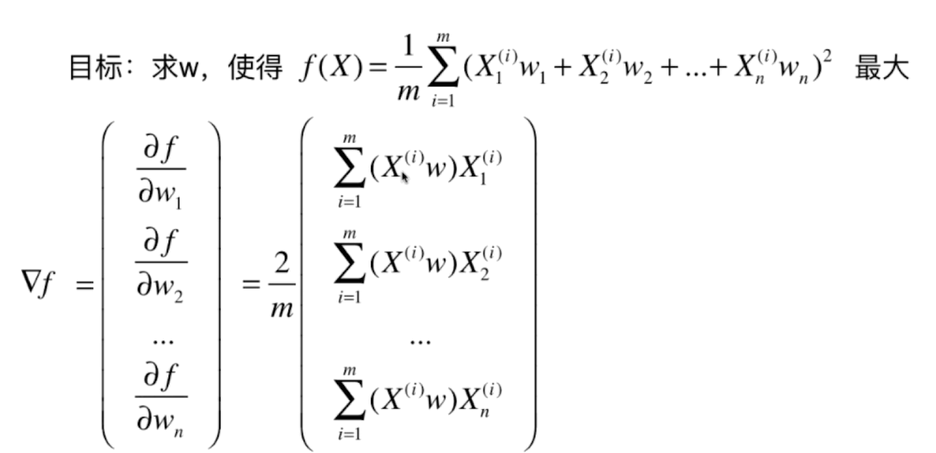
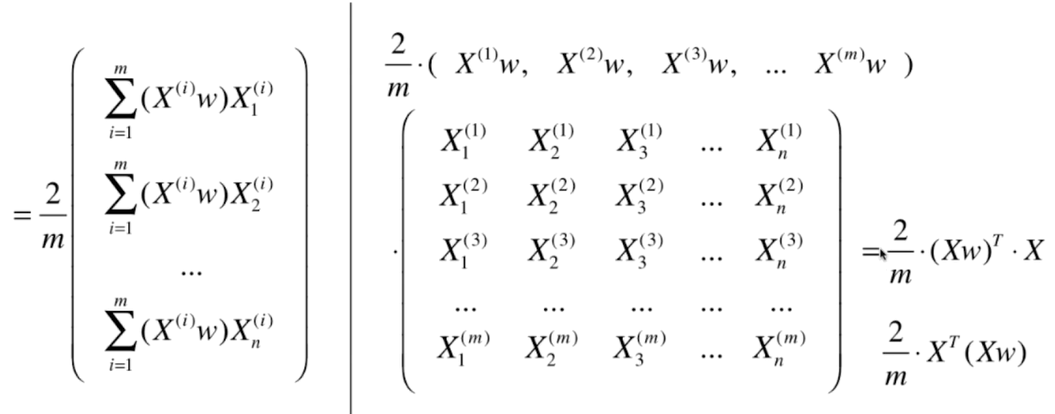
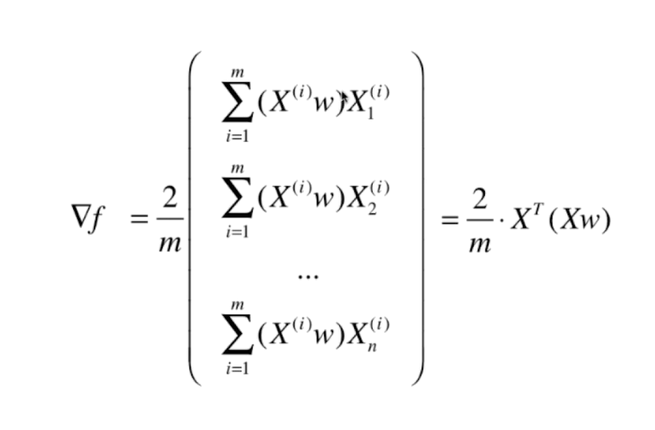
三、求数据的主成分PCA

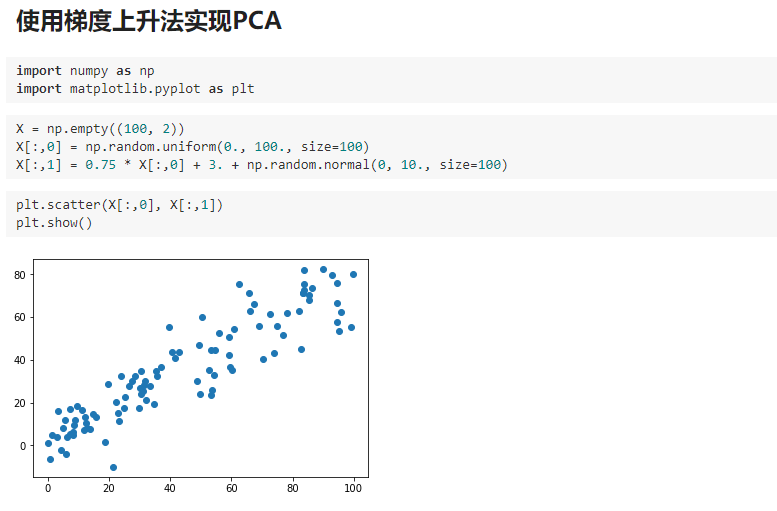
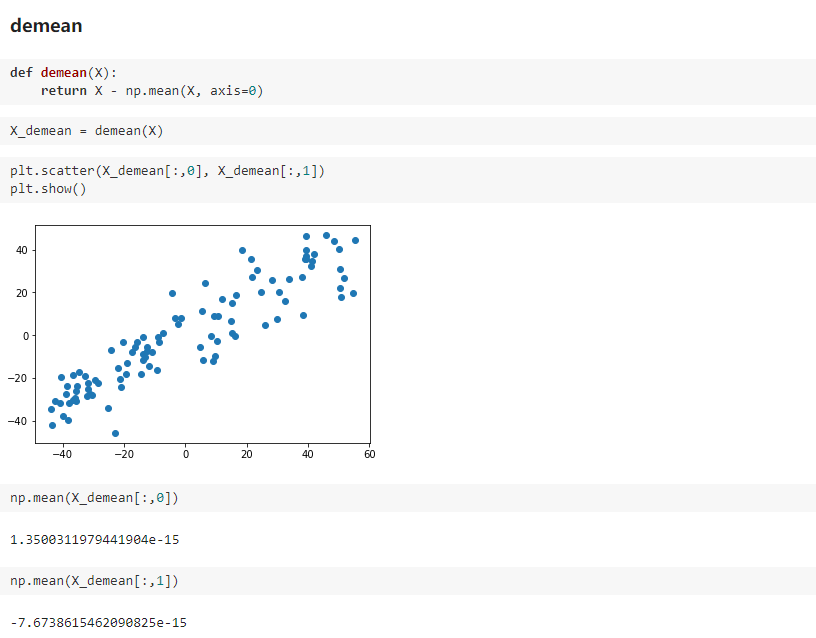
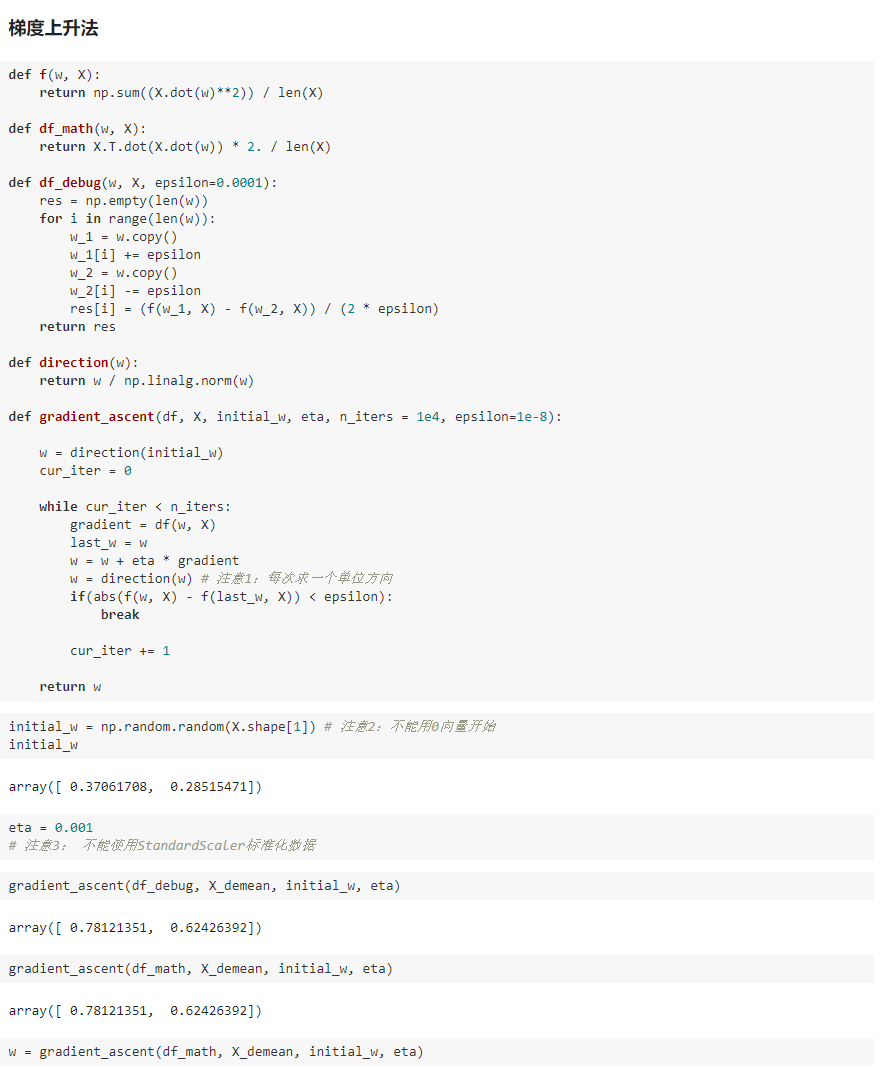
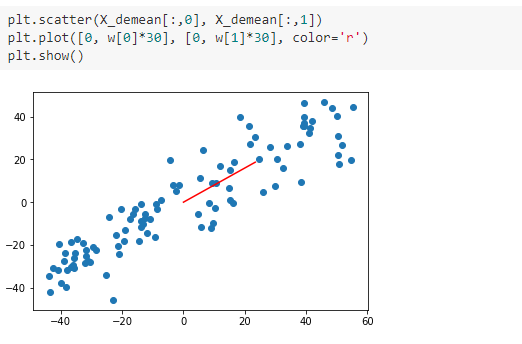
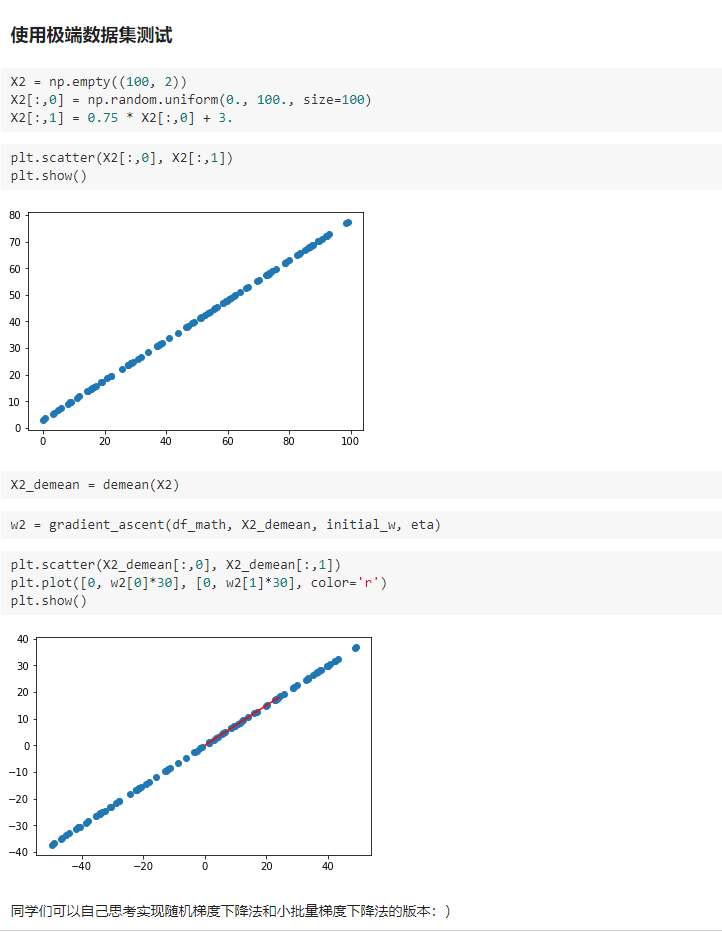
四、求数据的主成分 PCA

求数据的前 N 个主成分

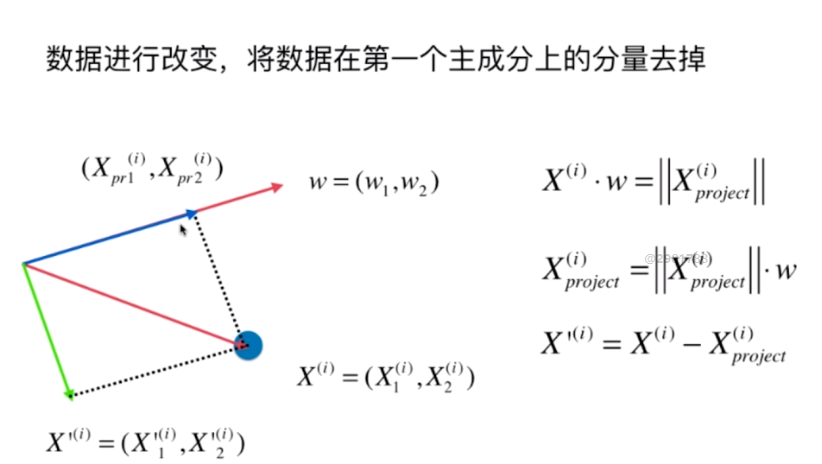
求出第一个主成分以后，如何求出下一个主成分？

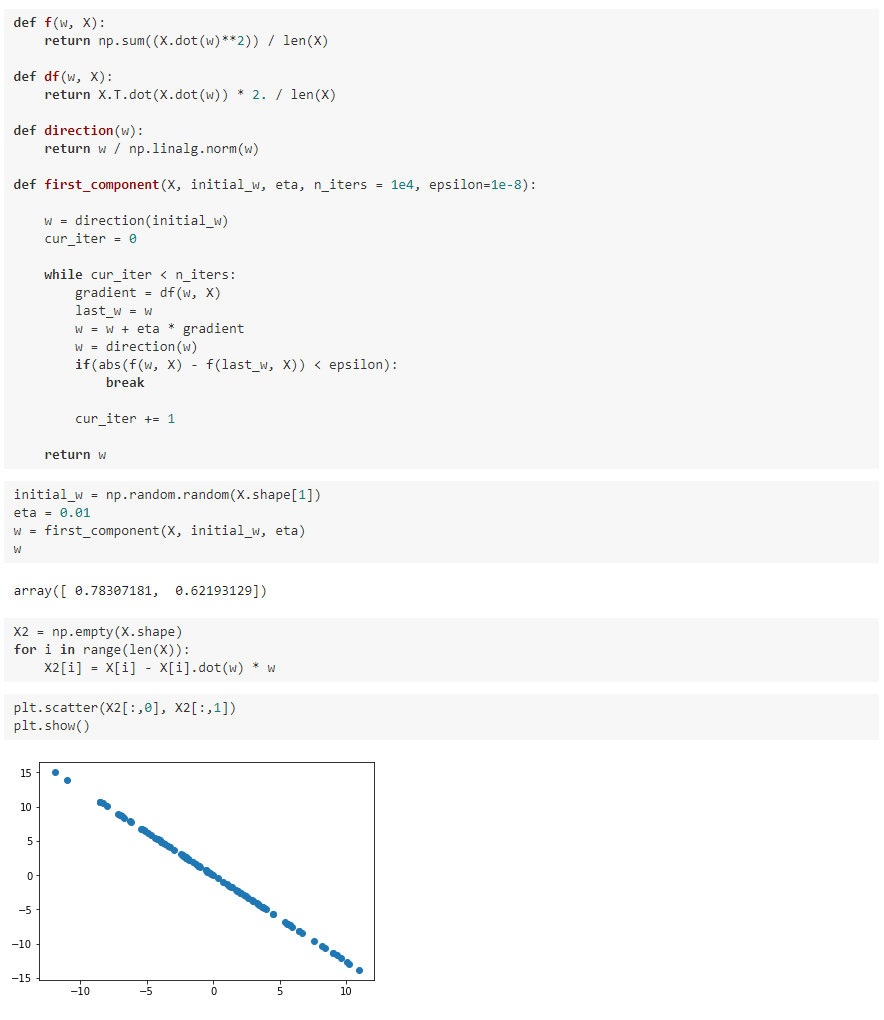
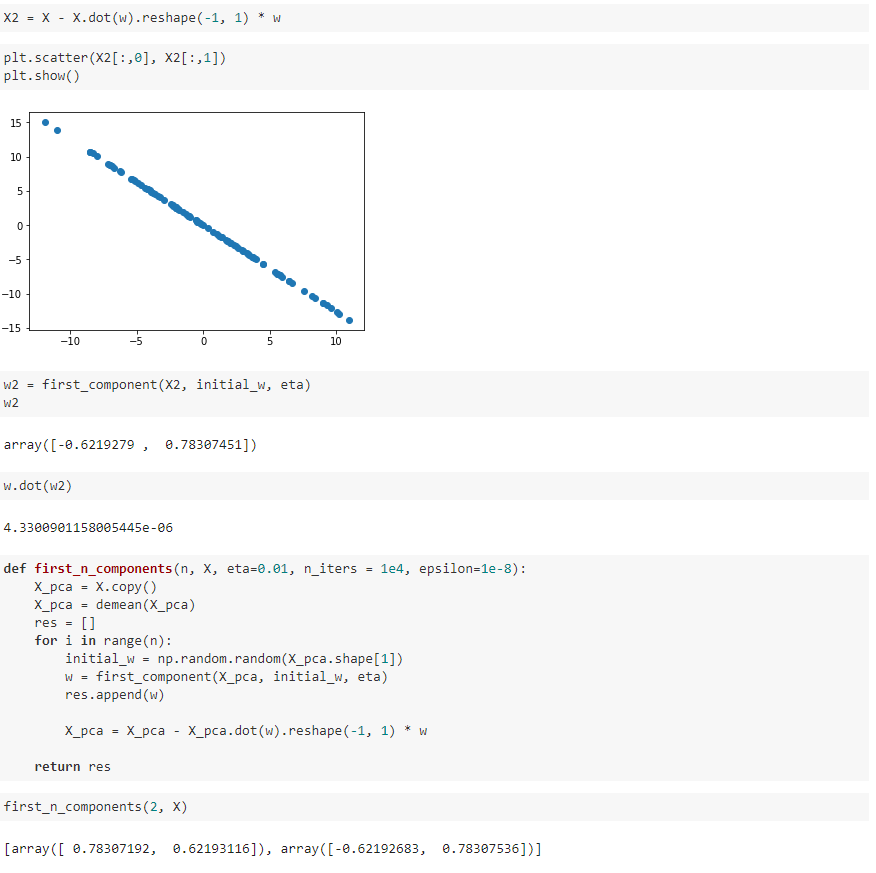
数据进行改变，将数据在第一个主成分的分量去掉。

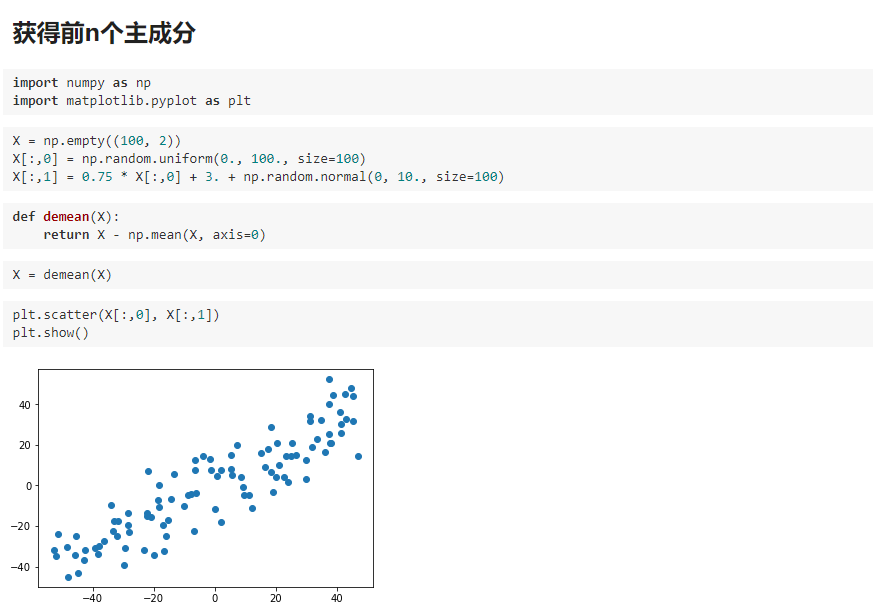
我写的文章只是我自己对bobo老师讲课内容的理解和整理，也只是我自己的弊见。bobo老师的课 是慕课网出品的。欢迎大家一起学习。

机器学习(七) PCA与梯度上升法 (上)的更多相关文章

  1. 机器学习(七) PCA与梯度上升法 (下)

    五.高维数据映射为低维数据 换一个坐标轴.在新的坐标轴里面表示原来高维的数据. 低维 反向 映射为高维数据 PCA.py import numpy as np class PCA: def __ini ...

  2. 机器学习（4）——PCA与梯度上升法

    主成分分析(Principal Component Analysis) 一个非监督的机器学习算法 主要用于数据的降维 通过降维,可以发现更便于人类理解的特征 其他应用:可视化.去噪 通过映射,我们可以 ...

  3. 4.pca与梯度上升法

    (一)什么是pca pca,也就是主成分分析法(principal component analysis),主要是用来对数据集进行降维处理.举个最简单的例子,我要根据姓名.年龄.头发的长度.身高.体重 ...

  4. 第7章 PCA与梯度上升法

    主成分分析法:主要作用是降维 疑似右侧比较好? 第三种降维方式: 问题:????? 方差:描述样本整体分布的疏密的指标,方差越大,样本之间越稀疏:越小,越密集 第一步: 总结: 问题:????怎样使其 ...

  5. 机器学习：PCA（使用梯度上升法求解数据主成分 Ⅰ ）

    一.目标函数的梯度求解公式 PCA 降维的具体实现,转变为: 方案:梯度上升法优化效用函数,找到其最大值时对应的主成分 w : 效用函数中,向量 w 是变量: 在最终要求取降维后的数据集时,w 是参数 ...

  6. 机器学习：PCA（高维数据映射为低维数据 封装&调用）

    一.基础理解 1) PCA 降维的基本原理 寻找另外一个坐标系,新坐标系中的坐标轴以此表示原来样本的重要程度,也就是主成分:取出前 k 个主成分,将数据映射到这 k 个坐标轴上,获得一个低维的数据集. ...

  7. 机器学习：PCA（基础理解、降维理解）

    PCA(Principal Component Analysis) 一.指导思想 降维是实现数据优化的手段,主成分分析(PCA)是实现降维的手段: 降维是在训练算法模型前对数据集进行处理,会丢失信息. ...

  8. 机器学习算法-PCA降维技术

    机器学习算法-PCA降维 一.引言 在实际的数据分析问题中我们遇到的问题通常有较高维数的特征,在进行实际的数据分析的时候,我们并不会将所有的特征都用于算法的训练,而是挑选出我们认为可能对目标有影响的特 ...

  9. 机器学习算法的调试---梯度检验（Gradient Checking）

    梯度检验是一种对求导结果进行数值检验的方法,该方法可以验证求导代码是否正确. 1. 数学原理   考虑我们想要最小化以 θ 为自变量的目标函数 J(θ)(θ 可以为标量和可以为矢量,在 Numpy 的 ...

随机推荐

  1. linux文件上传下载

    上传本地文件到服务器:scp 文件名 账号@服务器IP:文件路径eg:scp test.txt root@192.168.0.123:/tmp/服务器文件下载到本地:scp 账号@服务器IP:文件 本 ...

  2. POJ 3213 矩阵乘法（优化）

    思路: 1.暴力出奇迹 n=1000 n^3矩阵乘法竟然能卡过...(Tips:不要乱写读入优化,这玩意儿加了超时,不加AC--) 2. 注意题目中的"最多只能有一个地方不一样,," ...

  3. 【原创】rman备份出现ORA-19625

    [oracle@sunny stage]$ rman target / Recovery Manager: Release 10.2.0.1.0 - Production on Sun Mar 18 ...

  4. asp.net HTTP请求过程

    http://blog.csdn.net/zxxSsdsd/article/details/51909860

  5. 《Unix环境高级编程》读书笔记 第10章-信号

    1.引言 信号是软件中断. 信号提供了一种处理异步事件的方法. 2. 信号概念 信号的名字都是以3个字符SIG开头. Linux3.2.0支持31种信号.FreeBSD.Linux和Solaris作为 ...

  6. tigergao

    互联网从业 6 年.前码农&DBA,现运维&电商创业者,也在做自媒体.终生学习者. 运营微信公众号:高哥咋么看 感兴趣的朋友们可以订阅.

  7. 洛谷 P1967 货车运输 LCA + 最小生成树

    两点之间边权最大值的最小值一定在图的最小生成树中取到. 求出最小生成树,进行倍增即可. Code: #include<cstdio> #include<algorithm> u ...

  8. pyftpdlib 搭建ftp环境

    环境搭建: pythonwindows/linuxpip install pyftpdlib (安装失败请到这里下载:https://pypi.python.org/pypi/pyftpdlib/)一 ...

  9. IFC2x3标准阅读

    参考地址:西北逍遥-IFC数据模式架构的四个概念层详解说明 1.架构图 IFC模型体系结构由四个层次构成,从下到上依次是 资源层(Resource Layer).核心层(Core Layer).交互层 ...

  10. mysql 临时表和内存表

    查看内存表的最大值: show variables like '%heap%'; mysql> show variables like '%heap%'; +------------------ ...