hdu4767_Bell_矩阵快速幂+中国剩余定理

2013长春赛区网络赛的1009题

比赛的时候这道题英勇的挂掉了，原因是写错了一个系数，有时候粗心比脑残更可怕

本题是关于Bell数，关于Bell数的详情请见维基：http://en.wikipedia.org/wiki/Bell_number

其中有一句话是这么说的： And they satisfy "Touchard's congruence": If p is any prime bumber then

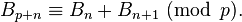
但95041567不是素数， 分解之后发现 95041567 = 31 × 37 × 41 × 43 × 47

按照上述递推式，利用矩阵快速幂可以得到 B_n mod p, (p = 31, 37, 41, 43, 47)，因为p最大47,所以矩阵快速幂O(p^3 * log(n/p))不会超时，

当然要先利用以下公式把B1-B47预处理出来：

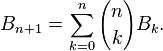
得到5个B_n mod p (p = 31, 37, 41, 43, 47)之后，怎样得到B_n mod  Πp 呢？

利用中国剩余定理可以完美的解决上述问题

详情见代码：

#include <cstdio>
#include <cstring>

#define MOD 95041567
#define LL long long

const int maxn = 50; //必须加 const，否则编译错误
LL x[5] = {31, 37, 41, 43, 47};
LL X;

class Matrix {
public:
    LL val[maxn][maxn];
    Matrix() {
        memset(val, 0, sizeof(val));
    }

    Matrix operator*(const Matrix& c) const {
        Matrix res;
        for (int i = 0; i < X; ++i)
            for (int j = 0; j < X; ++j)
                for (int k = 0; k < X; ++k) {
                    res.val[i][j] += val[i][k] * c.val[k][j];
                    res.val[i][j] = (res.val[i][j] + X) % X; //防止矩阵元素变为负数，若不需要，去掉"+MOD"
                }
        return res;
    }

    Matrix operator*=(const Matrix& c) {
        *this = *this * c;
        return *this;
    }

    Matrix Pow(LL k) { //返回one^k
        Matrix res = Zero();
        Matrix step = One();
        while (k) {
            if (k & 1)
                res *= step;
            k >>= 1;
            step *= step;
        }
        return res;
    }

    Matrix Zero() const {
        Matrix res;
        for (int i = 0; i < X; ++i)
            res.val[i][i] = 1;
        return res;
    }

    Matrix One() const {
        Matrix res;
        for (int i = 0; i < X - 1; ++i)
            res.val[i][i] = res.val[i + 1][i] = 1;
        res.val[0][X - 1] = res.val[1][X - 1] = res.val[X - 1][X - 1] = 1;
        return res;
    }
};

void gcd(LL a, LL b, LL& d, LL& xx, LL& y) {
    if (!b) {
        d = a, xx = 1, y = 0;
    } else {
        gcd(b, a % b, d, y, xx);
        y -= xx * (a / b);
    }
}

LL china(LL n, LL* a, LL* m) {
    LL M = 1, d, xx = 0, y;
    for (int i = 0; i < n; ++i) M *= m[i];
    for (int i = 0; i < n; ++i) {
        LL w = M / m[i];
        gcd(m[i], w, d, d, y);
        xx = (xx + y * w * a[i]) % M;
    }
    return (xx + M) % M;
}

LL c[50][50], f[50], a[5];

int main() {
    int T;
    for (int i = 0; i < 50; ++i) {
        c[i][0] = c[i][i] = 1;
        for (int j = 1; j < i; ++j)
            c[i][j] = (c[i-1][j] + c[i - 1][j - 1]) % MOD;
    }
    f[0] = 1;
    f[1] = 1;
    for (int i = 2; i < 50; ++i) {
        for (int j = 0; j < i; ++j)
            f[i] = (f[i] + c[i - 1][j] * f[j]) % MOD;
    }
    scanf("%d", &T);
    while (T--) {
        LL n;
        scanf("%I64d", &n);
        if (n < 50) {
            printf("%I64d\n", f[n]);
            continue;
        }
        memset(a, 0 ,sizeof(a));
        for (int i = 0; i < 5; ++i) {
            X = x[i];
            Matrix m;
            m = m.Pow(n / X);
            for (int j = 0; j < X; ++j)
                a[i] = (a[i] + f[j] * m.val[j][n % X]) % X;
        }
        printf("%I64d\n", china(5, a, x));
    }
    return 0;
}