[luogu 1270] “访问”美术馆 (树形dp)

传送门

Description

经过数月的精心准备，Peer Brelstet，一个出了名的盗画者，准备开始他的下一个行动。艺术馆的结构，每条走廊要么分叉为两条走廊，要么通向一个展览室。Peer知道每个展室里藏画的数量，并且他精确测量了通过每条走廊的时间。由于经验老到，他拿下一幅画需要5秒的时间。你的任务是编一个程序，计算在警察赶来之前，他最多能偷到多少幅画。

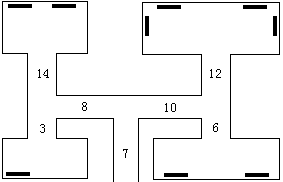
Input

第1行是警察赶到的时间，以s为单位。第2行描述了艺术馆的结构，是一串非负整数，成对地出现：每一对的第一个数是走过一条走廊的时间，第2个数是它末端的藏画数量；如果第2个数是0，那么说明这条走廊分叉为两条另外的走廊。数据按照深度优先的次序给出，请看样例。

一个展室最多有20幅画。通过每个走廊的时间不超过20s。艺术馆最多有100个展室。警察赶到的时间在10min以内。

Output

输出偷到的画的数量

Sample Input

60

7 0 8 0 3 1 14 2 10 0 12 4 6 2

Sample Output

2

Solution

dfs时记录到这个节点最多剩多长时间

然后枚举这个节点和它子节点（如果有的话）的消耗时间直接转移即可

PS:本来想着做几道做几道比较水的树形dp结果。。WA三次QAQ,查了半天代码最后绝望去看题解发现由于要“在警察赶来之前”所以输入的时间要-1。。,好吧是我太蠢了QAQ

Code

//By Menteur_Hxy
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define int long long
#define ls nd[x][0]
#define rs nd[x][1]
#define F(i,a,b) for(register int i=(a);i<=(b);i++)
using namespace std;

int read() {
	int x=0,f=1; char c=getchar();
	while(!isdigit(c)) {if(c=='-') f=-f; c=getchar();}
	while(isdigit(c)) x=(x<<1)+(x<<3)+c-48,c=getchar();
	return x*f;
}

const int N=110;
int T,tot=1;
int nd[N<<2][2],ti[N<<2],pi[N<<2],dp[N<<2][6010];

void build(int x) {
	ti[x]=read(),pi[x]=read();
	if(!pi[x]) ls=++tot,build(tot),rs=++tot,build(tot);
}

void dfs(int x,int t) {
	if(pi[x]) F(i,ti[x]*2+1,min(t,ti[x]*2+5*pi[x])) dp[x][i]=(i-ti[x]*2)/5;
	else if(t>ti[x]*2) {
		dfs(ls,t-ti[x]*2); dfs(rs,t-ti[x]*2);
		F(i,ti[x]*2+1,t) F(j,0,i-ti[x]*2)
			dp[x][i]=max(dp[x][i],dp[ls][j]+dp[rs][i-ti[x]*2-j]);
	}
//	cout<<t<<endl;
//	F(i,1,t) if(dp[x][i]) printf("dp[%d][%d]=%d\n",x,i,dp[x][i]);
}

signed main() {
	scanf("%lld",&T);
	build(1);
	dfs(1,T);
	printf("%lld",dp[1][T-1]);//要-1 QAQ
	return 0;
}