Quoit Design (HDU 1007)平面的最近点对

题目大意：
给定平面上的 n 个点，求距离最近的两个点的距离的一半。 n <= 10^5.

 

---

晕乎乎的度过了一上午。。。

总之来学习下分治吧233

分治就是把大问题拆成小问题，然后根据对小问题处理出的结果合并成大问题的答案

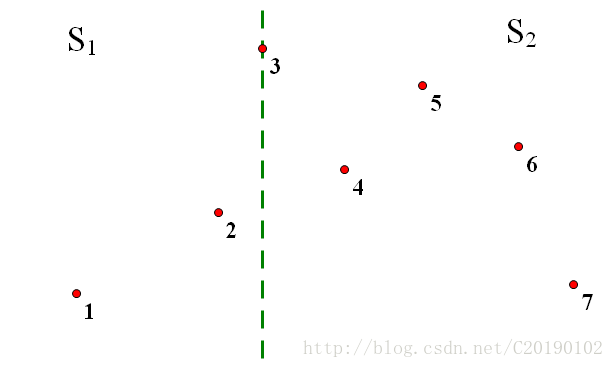
比如说这道题，如果我们按照X坐标把所有的点分成两组：

（木哈哈请叫我盗图狂魔○( ＾皿＾)っHiahiahia…

像上面我们把点分成了集合S1，S2

点对对应的被划分成3种：S1内，S2内，跨S1.S2

那假若我们分别处理出了S1，S2内的答案，再取个min叫做d

那么跨过分界线的点对就不能超过d，这是一个很有用的条件！不信？我们来看看

我们管分界线的X坐标叫x0

首先要知道，所有距离x0超过d的点都不用考虑

其次，这些点之间y的相对距离超过d的也不用考虑

这就把对一个点而言需要考虑的另一个点们限制在了一个小矩形里

再加上d是我们左右分治出来的答案

结论就是对于一个点我们最多只需要考虑6个点就可以了

你可以自己画画？这六个点都分布在矩形的顶点上

而具体实现其实就简单暴力了

具体就看码吧~

 #include<cmath>
 #include<cstdio>
 #include<algorithm>
 using namespace std;
 int n,cnt;
 struct point{
     double x,y;
 }p[];
 int mk[];
 bool cmpx(point A,point B){return A.x<B.x;}
 bool cmpy(int A,int B){return p[A].y<p[B].y;}
 double dis(int x,int y){return sqrt((p[x].x-p[y].x)*(p[x].x-p[y].x)+(p[x].y-p[y].y)*(p[x].y-p[y].y));}
 double solve(int l,int r){
     if(l==r)return 1e18;
     if(l+==r)return dis(l,r);
     int mid=(l+r)>>;
     double x0=(p[mid].x+p[mid+].x)/2.0;
     double d=min(solve(l,mid),solve(mid+,r));
     cnt=;
     for(int i=l;i<=r;i++)
     if(p[i].x-x0<=d&&p[i].x-x0>=-d)
     mk[++cnt]=i;
     sort(mk+,mk++cnt,cmpy);
     for(int i=;i<=cnt;i++)
     for(int j=i-;j>=;j--)
     if(p[mk[i]].y-p[mk[j]].y>d)break;
     else d=min(d,dis(mk[i],mk[j]));
     return d;
 }
 int main(){
     scanf("%d",&n);
     for(int i=;i<=n;i++)scanf("%lf%lf",&p[i].x,&p[i].y);
     sort(p+,p++n,cmpx);
     printf("%.4lf",solve(,n));
     return ;
 }