基于python的数学建模---运输问题

代码

import pulp
import numpy as np
from pprint import pprint

def transport_problem(costs, x_max, y_max):
    row = len(costs)
    col = len(costs[0])
    prob = pulp.LpProblem('Transportation Problem', sense=pulp.LpMaximize)
    var = [[pulp.LpVariable(f'x{i}{j}', lowBound=0, cat=pulp.LpInteger)
            for j in range(col)] for i in range(row)]
    flatten = lambda x: [y for l in x for y in flatten(l)] if type(x) is list else [x]#定义一个x，x若为列表形式则执行for循环，flatten将多维数组转换为一维数组
    prob += pulp.lpDot(flatten(var), costs.flatten())#costs是numpy定义的，有自己的函数
    for i in range(row):
        prob += (pulp.lpSum(var[i])) <= x_max[i]
    for j in range(col):
        prob += (pulp.lpSum(var[i][j] for i in range(row)) <= y_max[j])
    prob.solve()
    return {'objective': pulp.value(prob.objective), 'var': [[pulp.value(var[i][j]) for j in range(col)] for
                                                               i in range(row)]}

if __name__ == '__main__':
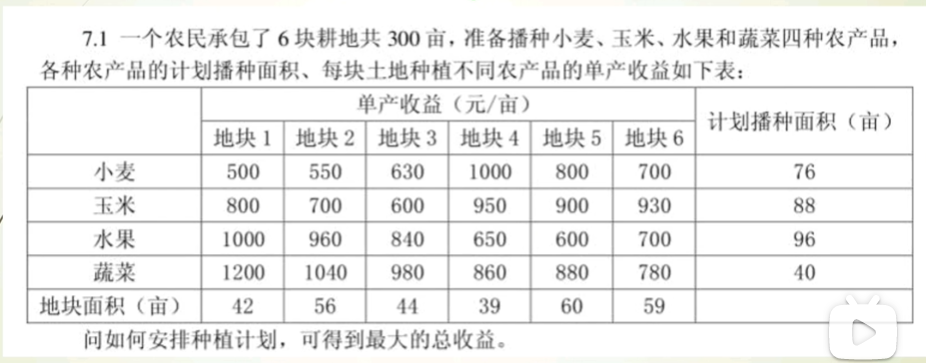
    costs = np.array([[500, 550, 630, 1000, 800, 700],
                      [800, 700, 600, 950, 900, 930],
                      [1000, 960, 840, 650, 600, 700],
                      [1200, 1040, 980, 860, 880, 780]])
    max_plant = [76, 88, 96, 40]
    max_cultivation = [42, 56, 44, 39, 60, 59]
    res = transport_problem(costs, max_plant, max_cultivation)
    print(f'最大值为{res["objective"]}')
    print('各变量的取值为: ')
    pprint(res['var'])

最大值为284230.0
各变量的取值为:
[[0.0, 0.0, 6.0, 39.0, 31.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 29.0, 59.0],
[2.0, 56.0, 38.0, 0.0, 0.0, 0.0],
[40.0, 0.0, 0.0, 0.0, 0.0, 0.0]]