7、Taylor公式(泰勒公式)通俗+本质详解
参考:https://zhuanlan.zhihu.com/p/392808684
1、比较通俗地讲解一下泰勒公式是什么。
泰勒公式,也称泰勒展开式。是用一个函数在某点的信息,描述其附近取值的公式。如果函数足够平滑,在已知函数在某一点的各阶导数值的情况下,泰勒公式可以利用这些导数值来做系数,构建一个多项式近似函数,求得在这一点的邻域中的值。
所以泰勒公式是做什么用的?
简单来讲就是用一个多项式函数去逼近一个给定的函数 ( 即尽量使多项式函数图像拟合给定的函数图像 ) ,注意,逼近的时候一定是从函数图像上的某个点展开。如果一个非常复杂的函数,想求其某点的值,直接求无法实现,这时候可以使用泰勒公式去近似的求该值,这是泰勒公式的应用之一。泰勒公式在机器学习中主要应用于梯度迭代。
2、问题的提出
多项式 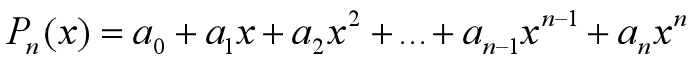 是最简单的一类初等函数。关于多项式,由于它本身的运算仅是有限项加减法和乘法,所以在数值计算方面,多项式是人们乐于使用的工具。因此我们经常用多项式来近似表达函数。这也是为什么泰勒公式选择多项式函数去近似表达给定的函数。
是最简单的一类初等函数。关于多项式,由于它本身的运算仅是有限项加减法和乘法,所以在数值计算方面,多项式是人们乐于使用的工具。因此我们经常用多项式来近似表达函数。这也是为什么泰勒公式选择多项式函数去近似表达给定的函数。
3、近似计算举例
初等数学已经了解到一些函数如: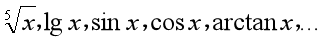 的一些重要性质,但是初等数学不曾回答怎样来计算它们,以
的一些重要性质,但是初等数学不曾回答怎样来计算它们,以 的近似计算为例:
的近似计算为例:
①一次(线性逼近)
利用微分近似计算公式 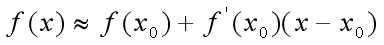 ,( 该式由导数/微分的极限表达公式转换得到 ),对
,( 该式由导数/微分的极限表达公式转换得到 ),对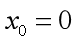 附近的
附近的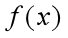 的线性逼近为:
的线性逼近为: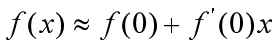 ,所以
,所以 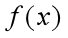 在
在 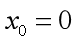 附近的线性逼近函数
附近的线性逼近函数 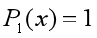 ,如下图:
,如下图:
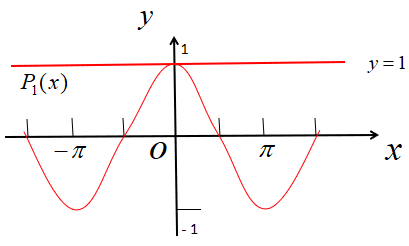
线性逼近优点:形式简单,计算方便;缺点:离原点 O 越远,近似度越差。
②二次逼近
二次多项式 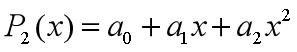 逼近
逼近 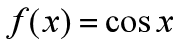 ,我们期望:
,我们期望:
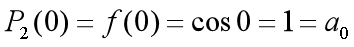 (即期望在
(即期望在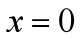 处逼近函数和给定函数值相等);
处逼近函数和给定函数值相等);
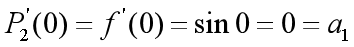 (即期望在
(即期望在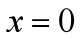 处逼近函数和给定函数的斜率相等);
处逼近函数和给定函数的斜率相等);
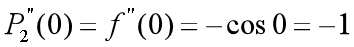 ,所以
,所以  (即期望在
(即期望在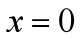 处逼近函数和给定函数的曲率相等);
处逼近函数和给定函数的曲率相等);
所以 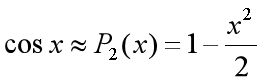 ,如下图
,如下图
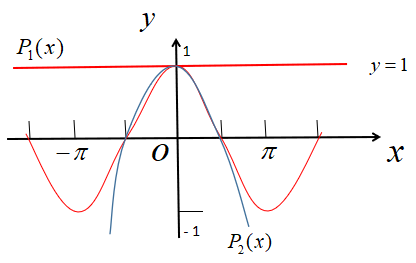
二次逼近要比线性逼近好得多,但局限于 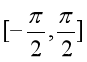 内,该范围外,图像明显差异很大。为什么我们期望两个函数在某一点的函数值、一阶导数值、二阶导数值相等?因为这些值表达了函数(图像)最基本和最主要的性质,这些性质逼近即可使两个函数逼近(由上图函数图像可以直观地看出来)
内,该范围外,图像明显差异很大。为什么我们期望两个函数在某一点的函数值、一阶导数值、二阶导数值相等?因为这些值表达了函数(图像)最基本和最主要的性质,这些性质逼近即可使两个函数逼近(由上图函数图像可以直观地看出来)
③八次逼近
八次多项式 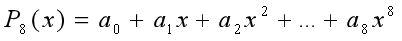 逼近
逼近 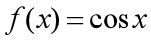 ,我们期望:
,我们期望:
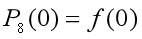 ,求出
,求出 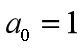 (即期望在
(即期望在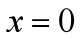 处逼近函数和给定函数值相等);
处逼近函数和给定函数值相等);
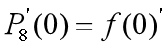 ,求出
,求出 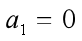 (即期望在
(即期望在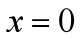 处逼近函数和给定函数的斜率相等);
处逼近函数和给定函数的斜率相等);

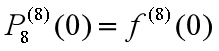 ,求出
,求出 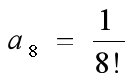 (即期望在
(即期望在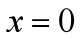 处逼近函数和给定函数的曲率相等);
处逼近函数和给定函数的曲率相等);
所以 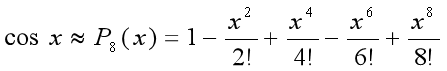 ,如下图:
,如下图:
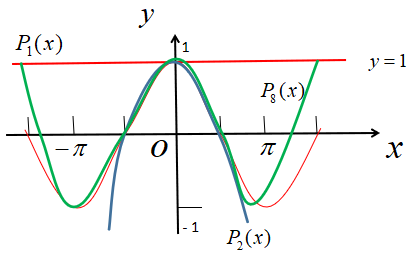
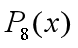 (绿色图像)比
(绿色图像)比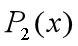 (蓝色图像)更大范围内更接近余弦函数(红色图像)
(蓝色图像)更大范围内更接近余弦函数(红色图像)
由上述3次不同程度的函数逼近可以看出:对于精确度要求较高且需要估计误差的时候,必须用高次多项式来近似表达函数,同时给出误差公式。
以上就是利用多项式函数去逼近给定函数的一个过程。
4、泰勒公式的推导
由此引出一个问题:给定一个函数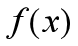 ,要找一个在指定点
,要找一个在指定点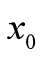 附近与
附近与 很近似的多项式函数
很近似的多项式函数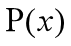 ,记为:
,记为: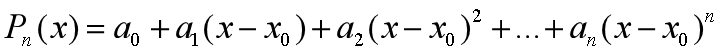 使得
使得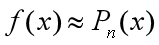 并且使得两者误差
并且使得两者误差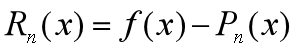 可估计。所以要找的多项式应该满足什么条件,误差是什么?
可估计。所以要找的多项式应该满足什么条件,误差是什么?
从几何上看,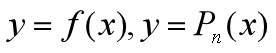 代表两条曲线,如下图:
代表两条曲线,如下图:
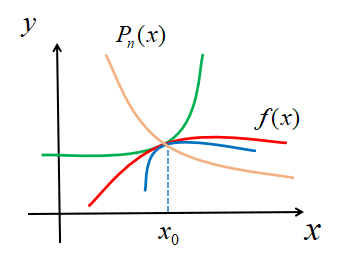
使它们在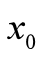 附近很靠近,很明显:
附近很靠近,很明显:
① 首先要求两曲线在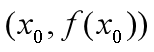 点相交,即
点相交,即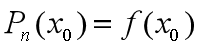
② 如果要靠得更近,还要求两曲线在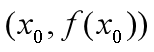 点相切,(由图像可以直观看出,相交【棕色和红色图像】和相切【绿色和红色图像】,两曲线在
点相切,(由图像可以直观看出,相交【棕色和红色图像】和相切【绿色和红色图像】,两曲线在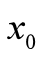 附近的靠近情况明显差异很大,相切更近),即
附近的靠近情况明显差异很大,相切更近),即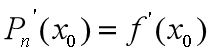
③ 如果还要靠得更近,还要求曲线在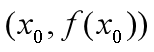 点弯曲方向相同,(如上图,弯曲方向相反【绿色和红色图像】;弯曲方向相同【蓝色和红色图像】,明显在离
点弯曲方向相同,(如上图,弯曲方向相反【绿色和红色图像】;弯曲方向相同【蓝色和红色图像】,明显在离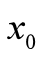 很远的地方,弯曲方向相同两函数的差异更小一点),即
很远的地方,弯曲方向相同两函数的差异更小一点),即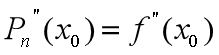 ,进而可猜想,若在
,进而可猜想,若在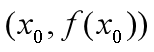 附近有
附近有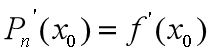 ,
,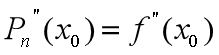 ,......,
,......,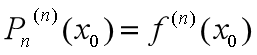 ,近似程度越来越好。
,近似程度越来越好。
综上所述,所要找的多项式应满足下列条件:
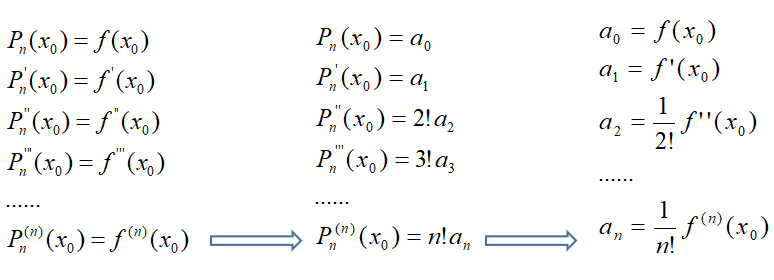
解释一下上面的转换是如何做的,以上面第三行的二阶导数为例:
第一个箭头的转换:将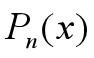 求二阶导函数后将
求二阶导函数后将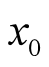 带入,求得
带入,求得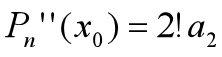
第二个箭头的转换:所以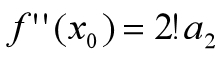 ,所以
,所以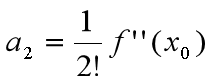
多项式函数 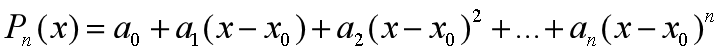 中的系数
中的系数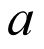 可以全部由
可以全部由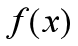 表示,则得到:
表示,则得到: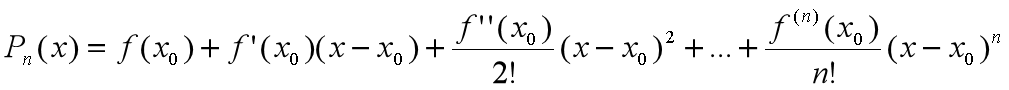
其中误差为 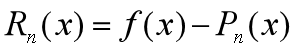 。因为是用多项式函数去无限逼近给定的函数,所以两者之间肯定存在一丢丢的误差。
。因为是用多项式函数去无限逼近给定的函数,所以两者之间肯定存在一丢丢的误差。
5、泰勒公式的定义
所以我们就得到了泰勒公式的定义:
如果函数 在含
在含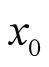 的某个开区间
的某个开区间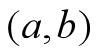 内具有直到
内具有直到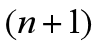 阶导数,则对
阶导数,则对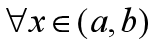 ,有
,有
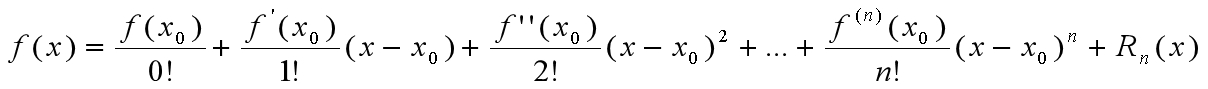
其中余项(即误差)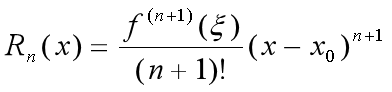 ,
,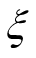 在
在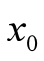 与
与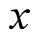 之间。泰勒公式的余项表达方式有好几种,前面这种表示方法称为
之间。泰勒公式的余项表达方式有好几种,前面这种表示方法称为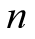 阶泰勒展开式的拉格朗日余项。拉格朗日余项是
阶泰勒展开式的拉格朗日余项。拉格朗日余项是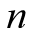 阶泰勒公式又多展开了一阶,
阶泰勒公式又多展开了一阶,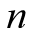 变为
变为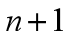 。注意,这里的余项即为误差,因为使用多项式函数在某点展开,逼近给定函数,最后肯定会有一丢丢的误差,我们称之为余项。
。注意,这里的余项即为误差,因为使用多项式函数在某点展开,逼近给定函数,最后肯定会有一丢丢的误差,我们称之为余项。
6、扩展--麦克劳林公式
是泰勒公式的一种特殊情况:即当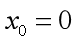 时的泰勒公式。所以将
时的泰勒公式。所以将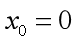 带入公式,即得:
带入公式,即得:
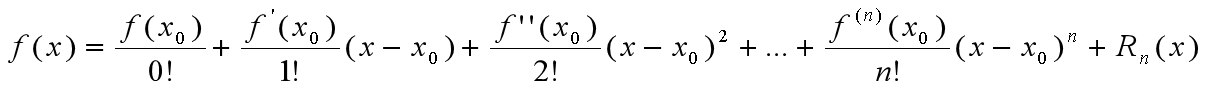
几个常见的初等函数的带有佩亚诺余项的麦克劳林公式:
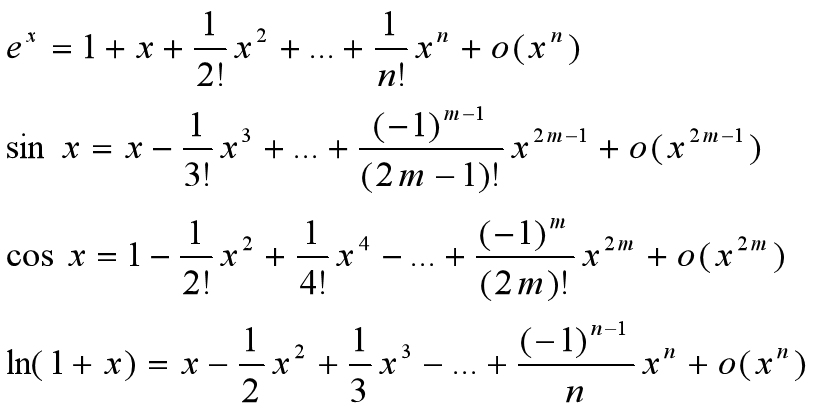
佩亚诺余项为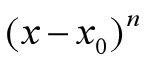 的高阶无穷小:
的高阶无穷小: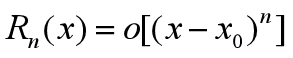
7、Taylor公式(泰勒公式)通俗+本质详解的更多相关文章
- EXC_BAD_ACCESS的本质详解以及僵尸模式调试原理
原文:What Is EXC_BAD_ACCESS and How to Debug It 有时候,你会遇到由EXC_BAD_ACCESS造成的崩溃. 这篇文章会告诉你什么是EXC_BAD_ACCES ...
- C# 委托/事件本质详解
委托 一.什么是委托 IL层面1>委托的本质就是一个类2>继承自System.MulticastDelegate3>委托里面内置了3个方法:Invoke(),BeginInvoke( ...
- golang中channels的本质详解,经典!
原文:https://www.goinggo.net/2014/02/the-nature-of-channels-in-go.html The Nature Of Channels In Go 这篇 ...
- HTTP POST GET 本质区别详解
HTTP POST GET 本质区别详解 一 原理区别 一般在浏览器中输入网址访问资源都是通过GET方式:在FORM提交中,可以通过Method指定提交方式为GET或者POST,默认为GET提交 Ht ...
- 转-HTTP POST GET SOAP本质区别详解
原文链接:HTTP POST GET SOAP本质区别详解 一 原理区别 一般在浏览器中输入网址访问资源都是通过GET方式:在FORM提交中,可以通过Method指定提交方式为GET或者POST,默认 ...
- 详解MathType中如何更改公式颜色
在MathType数学公式编辑器中可以通过更改公式颜色,起到美化.标注公式的效果.本教程将详解MathType中如何更改公式颜色. 点击菜单栏中的样式->格式->颜色,用户就可以根据自己的 ...
- 详解MathType引用公式编号功能
在论文创作期间,如果需要在文本中删除大量的公式,手动编号删除的工作量是比较大的,使用MathType引用公式编号功能就可以节约大量的时间,提供很大的方便.本教程将详解MathType引用公式编号功能. ...
- 详解MathType中如何批量修改公式字体和大小
MathType应用在论文中时,有时会因为排版问题批量修改公式字体和大小,一个一个的修改不仅费时费力,还容易出现错误,本教程将详解如何在MathType公式编辑器中批量修改公式字体和大小. MathT ...
- 详解在Word文档中常见的各种公式编辑问题
正常情况下,我们在安装完成MathType之后会直接加载在Word文档中,Word文档中的MathType比较复杂,新手操作遇到麻烦也是常有的事,今天就来给大家详解下Word文档中常见的MathTyp ...
- SIFT算法详解(转)
http://blog.csdn.net/zddblog/article/details/7521424 目录(?)[-] 尺度不变特征变换匹配算法详解 Scale Invariant Feature ...
随机推荐
- DataX插件二次开发指南
一. DataX为什么要使用插件机制? 从设计之初,DataX就把异构数据源同步作为自身的使命,为了应对不同数据源的差异.同时提供一致的同步原语和扩展能力,DataX自然而然地采用了框架 + 插件 的 ...
- 带你读AI论文丨S&P21 Survivalism: Living-Off-The-Land 经典离地攻击
摘要:这篇文章属于系统分析类的文章,通过详细的实验分析了离地攻击(Living-Off-The-Land)的威胁性和流行度,包括APT攻击中的利用及示例代码论证. 本文分享自华为云社区<[论文阅 ...
- DJI Flight Simulator 无人机模拟器 功能介绍与使用说明
0 前言 无人机是当前非常火热的"相机设备",而大疆又是其中翘楚,功能丰富,可以说是一个将带着云台的智能手机放到了天空中.如果你有自己玩过旋翼无人机航模的话,可能会体会到大疆的另一 ...
- pdf转图片加水印压缩
''' pip install pymupdf pip install pillow ''' import os import uuid import fitz from PIL import Ima ...
- MySQL-字段约束条件
1.无符号.零填充 1.unsigned:用在生成表的过程中,表示不取负数,只取正数和0,负数会直接报错,eg:id int unsigned. 2.zerofill:用在生成表的过程中,跟在整形2后 ...
- JavaScript是怎样实现继承的?
一.是什么 继承(inheritance)是面向对象软件技术当中的一个概念. 如果一个类别B"继承自"另一个类别A,就把这个B称为"A的子类",而把A称为&qu ...
- 微信小程序使用vant组件样式不生效的问题
下面提供几个解决方案 方案一: 官方文档有说明,将 app.json 中的 "style": "v2" 去除,小程序的新版基础组件强行加上了许多样式,难以覆盖, ...
- Training Spiking Neural Networks with Local Tandem Learning
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布! 36th Conference on Neural Information Processing Systems (NeurIPS 202 ...
- 教你用手机的NFC功能模拟门禁卡,实现出门不带卡
此教程教您将门禁卡.考勤卡.会员卡.停车卡.电梯卡等等各种卡片模拟进NFC手机里,从而用手机代替门禁卡 一.软硬件准备 NFC Tool 手机上的IC卡读写编辑软件,搭配蓝牙读卡器或者OTG读卡器,可 ...
- cmd数字雨原代码
转自:https://www.xitongtiandi.net/wenzhang/xp/29290.html
