迁移学习（DANN）《Domain-Adversarial Training of Neural Networks》

论文信息

论文标题：Domain-Adversarial Training of Neural Networks
论文作者：Yaroslav Ganin, Evgeniya Ustinova, Hana Ajakan, Pascal Germain, Hugo Larochelle....
论文来源： JMLR 2016
论文地址：download 
论文代码：download
引用次数：5292

1 Domain Adaptation

　　We consider classification tasks where $X$ is the input space and $Y=\{0,1, \ldots, L-1\}$ is the set of $L$ possible labels. Moreover, we have two different distributions over $X \times Y$ , called the source domain $\mathcal{D}_{\mathrm{S}}$ and the target domain $\mathcal{D}_{\mathrm{T}}$ . An unsupervised domain adaptation learning algorithm is then provided with a labeled source sample $S$ drawn i.i.d. from $\mathcal{D}_{\mathrm{S}}$ , and an unlabeled target sample $T$ drawn i.i.d. from $\mathcal{D}_{\mathrm{T}}^{X}$ , where $\mathcal{D}_{\mathrm{T}}^{X}$ is the marginal distribution of $\mathcal{D}_{\mathrm{T}}$ over $X$ .

　　　　$S=\left\{\left(\mathbf{x}_{i}, y_{i}\right)\right\}_{i=1}^{n} \sim\left(\mathcal{D}_{\mathrm{S}}\right)^{n}$

　　　　$T=\left\{\mathbf{x}_{i}\right\}_{i=n+1}^{N} \sim\left(\mathcal{D}_{\mathrm{T}}^{X}\right)^{n^{\prime}}$

　　with $N=n+n^{\prime}$ being the total number of samples. The goal of the learning algorithm is to build a classifier $\eta: X \rightarrow Y$ with a low target risk

　　　　$R_{\mathcal{D}_{\mathrm{T}}}(\eta)=\operatorname{Pr}_{(\mathbf{x}, y) \sim \mathcal{D}_{\mathrm{T}}}(\eta(\mathbf{x}) \neq y),$

　　while having no information about the labels of $\mathcal{D}_{\mathrm{T}}$ .

2 Domain Divergence

　　Definition 1. Given two domain distributions  $\mathcal{D}_{\mathrm{S}}^{X}$  and  $\mathcal{D}_{\mathrm{T}}^{X}$  over  $X$ , and a hypothesis class  $\mathcal{H}$ , the  $\mathcal{H}$ -divergence between  $\mathcal{D}_{\mathrm{S}}^{X}$  and  $\mathcal{D}_{\mathrm{T}}^{X}$  is

　　　　$d_{\mathcal{H}}\left(\mathcal{D}_{\mathrm{S}}^{X}, \mathcal{D}_{\mathrm{T}}^{X}\right)=    2 \text{sup}_{\eta \in \mathcal{H}}\left|\operatorname{Pr}_{\mathbf{x} \sim \mathcal{D}_{\mathrm{S}}^{X}}\; \;\; [\eta(\mathbf{x})=1]-\operatorname{Pr}_{\mathbf{x} \sim \mathcal{D}_{\mathrm{T}}^{X}} \; [\eta(\mathbf{x})=1]\right|$

　　该散度的意思是，在一个假设空间  $\mathcal{H}$  中，找到一个函数 $\mathrm{h}$，使得  $\operatorname{Pr}_{x \sim \mathcal{D}}[h(x)=1]$  的概率尽可能大，而  $\operatorname{Pr}_{x \sim \mathcal{D}^{\prime}}[h(x)=1]$  的概率尽可能小。【如果数据来自源域，域标签为 $1$，如果数据来自目标域，域标签为 $0$】也就是说，用最大距离来衡量  $\mathcal{D}, \mathcal{D}^{\prime}$  之间的距离。同时这个 $h$ 也可以理解为是用来尽可能区分  $\mathcal{D}$，$\mathcal{D}^{\prime}$  这两个分布的函数。

　　可以通过计算来计算两个样本 $S \sim\left(\mathcal{D}_{\mathrm{S}}^{X}\right)^{n}$ 和 $T \sim\left(\mathcal{D}_{\mathrm{T}}^{X}\right)^{n^{\prime}}$ 之间的经验 $\text { H-divergence }$：

　　　　$\hat{d}_{\mathcal{H}}(S, T)=2\left(1- \underset{\eta \in \mathcal{H}}{\text{min}} \left[\frac{1}{n} \sum\limits_{i=1}^{n} I\left[\eta\left(\mathbf{x}_{i}\right)=0\right]+\frac{1}{n^{\prime}} \sum\limits _{i=n+1}^{N} I\left[\eta\left(\mathbf{x}_{i}\right)=1\right]\right]\right) \quad\quad(1)$

　　其中，$I[a]$ 是指示函数，当 $a$ 为真时，$I[a] = 1$，否则 $I[a] = 0$。

3 Proxy Distance

　　由于经验 $\mathcal{H}$-divergence 难以精确计算，可以使用判别源样本与目标样本的学习算法完成近似。

　　构造新的数据集 $U$ ：

　　　　$U=\left\{\left(\mathbf{x}_{i}, 0\right)\right\}_{i=1}^{n} \cup\left\{\left(\mathbf{x}_{i}, 1\right)\right\}_{i=n+1}^{N}\quad\quad(2)$

　　使用 $\mathcal{H}$-divergence 的近似表示 Proxy A-distance（PAD），其中 $\epsilon$ 为 源域和目标域样本的分类泛化误差：

　　　　$\hat{d}_{\mathcal{A}}=2(1-2 \epsilon)\quad\quad(3)$

4 Method

　　为学习一个可以很好地从一个域推广到另一个域的模型，本文确保神经网络的内部表示不包含关于输入源（源或目标域）来源的区别信息，同时在源(标记)样本上保持低风险。

　　首先考虑一个标准的神经网络(NN)结构与一个单一的隐藏层。为简单起见，假设输入空间由 $m$ 维向量 $X=\mathbb{R}^{m}$ 构成。隐层 $G_{f}$ 学习一个函数  $G_{f}: X \rightarrow \mathbb{R}^{D}$ ，该函数将一个示例映射为一个 $\mathrm{d}$  维表示，并由矩阵-向量对 $  (\mathbf{W}, \mathbf{b}) \in \mathbb{R}^{D \times m} \times \mathbb{R}^{D}  $ 参数化：

　　　　$\begin{array}{l}G_{f}(\mathbf{x} ; \mathbf{W}, \mathbf{b})=\operatorname{sigm}(\mathbf{W} \mathbf{x}+\mathbf{b}) \\\text { with } \operatorname{sigm}(\mathbf{a})=\left[\frac{1}{1+\exp \left(-a_{i}\right)}\right]_{i=1}^{|\mathbf{a}|}\end{array}$

　　类似地，预测层 $G_{y}$ 学习一个函数 $G_{y}: \mathbb{R}^{D} \rightarrow[0,1]^{L}$，该函数由一对 $(\mathbf{V}, \mathbf{c}) \in \mathbb{R}^{L \times D} \times \mathbb{R}^{L}$：

　　　　$\begin{array}{l}G_{y}\left(G_{f}(\mathbf{x}) ; \mathbf{V}, \mathbf{c}\right)=\operatorname{softmax}\left(\mathbf{V} G_{f}(\mathbf{x})+\mathbf{c}\right)\\\text { with }\quad \operatorname{softmax}(\mathbf{a})=\left[\frac{\exp \left(a_{i}\right)}{\sum_{j=1}^{|a|} \exp \left(a_{j}\right)}\right]_{i=1}^{|\mathbf{a}|}\end{array}$

　　其中 $L=|Y|$。通过使用 softmax 函数，向量 $G_{y}\left(G_{f}(\mathbf{x})\right)$ 的每个分量表示神经网络将 $\mathbf{x}$ 分配给该分量在 $Y$ 中表示的类的条件概率。给定一个源样本 $\left(\mathbf{x}_{i}, y_{i}\right)$，使用正确标签的负对数概率：

　　　　$\mathcal{L}_{y}\left(G_{y}\left(G_{f}\left(\mathbf{x}_{i}\right)\right), y_{i}\right)=\log \frac{1}{G_{y}\left(G_{f}(\mathbf{x})\right)_{y_{i}}}$

　　对神经网络的训练会导致源域上的以下优化问题：

　　　　$\underset{\mathbf{W}, \mathbf{b}, \mathbf{V}, \mathbf{c}}{\text{min}} \left[\frac{1}{n} \sum_{i=1}^{n} \mathcal{L}_{y}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{V}, \mathbf{c})+\lambda \cdot R(\mathbf{W}, \mathbf{b})\right]$

　　其中，$\mathcal{L}_{y}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{V}, \mathbf{c})=\mathcal{L}_{y}\left(G_{y}\left(G_{f}\left(\mathbf{x}_{i} ; \mathbf{W}, \mathbf{b}\right) ; \mathbf{V}, \mathbf{c}\right), y_{i}\right)$，$R(\mathbf{W}, \mathbf{b})$ 是一个正则化项。

　　我们的方法的核心是设计一个直接从 Definition 1 的 $\mathcal{H}$-divergence 推导出的域正则化器。为此，我们将隐层 $G_{f}(\cdot)$（$\text{Eq.4}$）的输出视为神经网络的内部表示。因此，我们将源样本表示法表示为

　　　　$S\left(G_{f}\right)=\left\{G_{f}(\mathbf{x}) \mid \mathbf{x} \in S\right\}$

　　类似地，给定一个来自目标域的未标记样本，我们表示相应的表示形式

　　　　$T\left(G_{f}\right)=\left\{G_{f}(\mathbf{x}) \mid \mathbf{x} \in T\right\}$

　　在 $\text{Eq.1}$ 的基础上，给出了样本 $S\left(G_{f}\right)$ 和 $T\left(G_{f}\right)$ 之间的经验 $\mathcal{H}\text{-divergence}$：

　　　　$\hat{d}_{\mathcal{H}}\left(S\left(G_{f}\right), T\left(G_{f}\right)\right)=2\left(1-\min _{\eta \in \mathcal{H}}\left[\frac{1}{n} \sum\limits_{i=1}^{n} I\left[\eta\left(G_{f}\left(\mathbf{x}_{i}\right)\right)=0\right]+\frac{1}{n^{\prime}} \sum\limits_{i=n+1}^{N} I\left[\eta\left(G_{f}\left(\mathbf{x}_{i}\right)\right)=1\right]\right]\right) \quad\quad(6)$

　　域分类层 $G_{d}$ 学习了一个逻辑回归变量  $G_{d}: \mathbb{R}^{D} \rightarrow[0,1]$ ，其参数为 向量-常量对 $(\mathbf{u}, z) \in \mathbb{R}^{D} \times \mathbb{R}$，它模拟了给定输入来自源域 $\mathcal{D}_{\mathrm{S}}^{X}$ 或目标域 $\mathcal{D}_{\mathrm{T}}^{X}$ 的概率：

　　　　$G_{d}\left(G_{f}(\mathbf{x}) ; \mathbf{u}, z\right)=\operatorname{sigm}\left(\mathbf{u}^{\top} G_{f}(\mathbf{x})+z\right)\quad\quad(7)$

　　因此，函数 $G_{d}(\cdot)$ 是一个域回归器。我们定义它的损失是：

　　　　$\mathcal{L}_{d}\left(G_{d}\left(G_{f}\left(\mathbf{x}_{i}\right)\right), d_{i}\right)=d_{i} \log \frac{1}{G_{d}\left(G_{f}\left(\mathbf{x}_{i}\right)\right)}+\left(1-d_{i}\right) \log \frac{1}{1-G_{d}\left(G_{f}\left(\mathbf{x}_{i}\right)\right)}$

　　其中，$d_{i}$ 表示第 $i$ 个样本的二进制域标签，如果 $d_{i}=0$ 表示样本 $\mathbf{x}_{i}$ 是来自源分布 $\mathbf{x}_{i} \sim \mathcal{D}_{\mathrm{S}}^{X}$），如果 $d_{i}=1$ 表示样本来自目标分布 $\mathbf{x}_{i} \sim \mathcal{D}_{\mathrm{T}}^{X} $。

　　回想一下，对于来自源分布（$d_{i}=0$）的例子，相应的标签 $y_{i} \in Y$ 在训练时是已知的。对于来自目标域的例子，我们不知道在训练时的标签，而我们想在测试时预测这些标签。这使得我们能够在 $\text{Eq.5}$ 的目标中添加一个域自适应项，并给出以下正则化器：

　　　　$R(\mathbf{W}, \mathbf{b})=\underset{\mathbf{u}, z}{\text{max}}  {}\left[-\frac{1}{n} \sum\limits _{i=1}^{n} \mathcal{L}_{d}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{u}, z)-\frac{1}{n^{\prime}} \sum\limits_{i=n+1}^{N} \mathcal{L}_{d}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{u}, z)\right]\quad\quad(8)$

　　其中，$\mathcal{L}_{d}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{u}, z)=\mathcal{L}_{d}\left(G_{d}\left(G_{f}\left(\mathbf{x}_{i} ; \mathbf{W}, \mathbf{b}\right) ; \mathbf{u}, z\right), d_{i}\right)$ 。这个正则化器试图近似 $\text{Eq.6}$ 的 $\mathcal{H}\text{-divergence}$，因为 $2(1-R(\mathbf{W}, \mathbf{b}))$ 是 $\hat{d}_{\mathcal{H}}\left(S\left(G_{f}\right), T\left(G_{f}\right)\right)$ 的一个替代品。

　　为了学习，可以将 $\text{Eq.5}$ 的完整优化目标重写如下：

　　　　$\begin{array}{l}E(\mathbf{W}, \mathbf{V}, \mathbf{b}, \mathbf{c}, \mathbf{u}, z) \\\quad=\frac{1}{n} \sum\limits _{i=1}^{n} \mathcal{L}_{y}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{V}, \mathbf{c})-\lambda\left(\frac{1}{n} \sum\limits_{i=1}^{n} \mathcal{L}_{d}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{u}, z)+\frac{1}{n^{\prime}} \sum_{i=n+1}^{N} \mathcal{L}_{d}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{u}, z)\right)\end{array}\quad\quad(9)$

　　对应的参数优化 $\hat{\mathbf{W}}$, $\hat{\mathbf{V}}$, $\hat{\mathbf{b}}$, $\hat{\mathbf{c}}$, $\hat{\mathbf{u}}$, $\hat{z}$：

　　　　$\begin{array}{l}(\hat{\mathbf{W}}, \hat{\mathbf{V}}, \hat{\mathbf{b}}, \hat{\mathbf{c}}) & =&  \underset{\mathbf{W}, \mathbf{V}, \mathbf{b}, \mathbf{c}}{\operatorname{arg min}} E(\mathbf{W}, \mathbf{V}, \mathbf{b}, \mathbf{c}, \hat{\mathbf{u}}, \hat{z}) \\(\hat{\mathbf{u}}, \hat{z}) & =&\underset{\mathbf{u}, z}{\operatorname{arg max}} E(\hat{\mathbf{W}}, \hat{\mathbf{V}}, \hat{\mathbf{b}}, \hat{\mathbf{c}}, \mathbf{u}, z)\end{array}$

　　

Generalization to Arbitrary Architectures

　　分类损失和域分类损失：

　　　　$\begin{aligned}\mathcal{L}_{y}^{i}\left(\theta_{f}, \theta_{y}\right) & =\mathcal{L}_{y}\left(G_{y}\left(G_{f}\left(\mathbf{x}_{i} ; \theta_{f}\right) ; \theta_{y}\right), y_{i}\right) \\\mathcal{L}_{d}^{i}\left(\theta_{f}, \theta_{d}\right) & =\mathcal{L}_{d}\left(G_{d}\left(G_{f}\left(\mathbf{x}_{i} ; \theta_{f}\right) ; \theta_{d}\right), d_{i}\right)\end{aligned}$

　　优化目标：

　　　　$E\left(\theta_{f}, \theta_{y}, \theta_{d}\right)=\frac{1}{n} \sum\limits_{i=1}^{n} \mathcal{L}_{y}^{i}\left(\theta_{f}, \theta_{y}\right)-\lambda\left(\frac{1}{n} \sum\limits_{i=1}^{n} \mathcal{L}_{d}^{i}\left(\theta_{f}, \theta_{d}\right)+\frac{1}{n^{\prime}} \sum\limits_{i=n+1}^{N} \mathcal{L}_{d}^{i}\left(\theta_{f}, \theta_{d}\right)\right)  \quad\quad(10)$

　　对应的参数优化 $\hat{\theta}_{f}$, $\hat{\theta}_{y}$, $\hat{\theta}_{d}$：

　　　　$\begin{array}{l}\left(\hat{\theta}_{f}, \hat{\theta}_{y}\right) & =&\underset{\theta_{f}, \theta_{y}}{\operatorname{argmin}} E\left(\theta_{f}, \theta_{y}, \hat{\theta}_{d}\right) \quad\quad(11) \\\hat{\theta}_{d} & =&\underset{\theta_{d}}{\operatorname{argmax}} E\left(\hat{\theta}_{f}, \hat{\theta}_{y}, \theta_{d}\right)\quad\quad(12)\end{array}$

　　 如前所述，由 $\text{Eq.11-Eq.12}$ 定义的鞍点可以作为以下梯度更新的平稳点找到：

　　　　$\begin{array}{l}\theta_{f} \longleftarrow \theta_{f}-\mu\left(\frac{\partial \mathcal{L}_{y}^{i}}{\partial \theta_{f}}-\lambda \frac{\partial \mathcal{L}_{d}^{i}}{\partial \theta_{f}}\right)\quad\quad(13) \\\theta_{y} \longleftarrow \quad \theta_{y}-\mu \frac{\partial \mathcal{L}_{y}^{i}}{\partial \theta_{y}}\quad\quad\quad\quad \quad\quad(14)  \\\theta_{d} \quad \longleftarrow \quad \theta_{d}-\mu \lambda \frac{\partial \mathcal{L}_{d}^{i}}{\partial \theta_{d}}\quad\quad\quad\quad(15)  \\\end{array}$

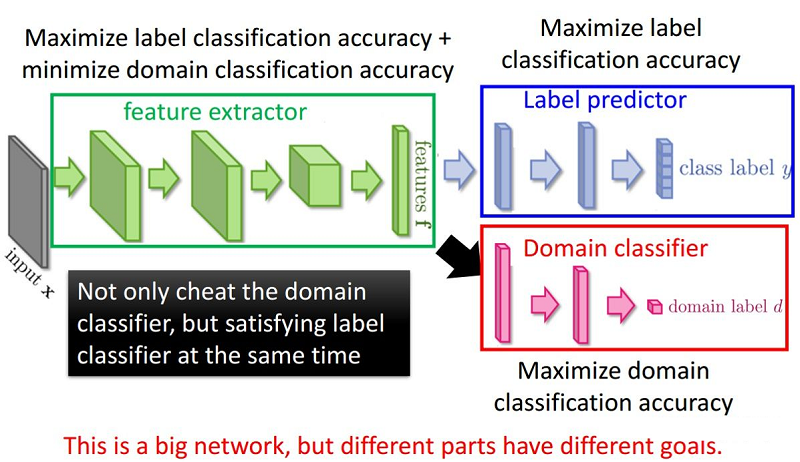
　　整体框架：

　　

　　组件：

• • 特征提取器（feature extractor）$G_{f}\left(\cdot ; \theta_{f}\right)$ ：将源域样本和目标域样本进行映射和混合，使域判别器无法区分数据来自哪个域；提取后续网络完成任务所需要的特征，使标签预测器能够分辨出来自源域数据的类别；
  • 标签预测器（label predictor）$G_{y}\left(\cdot ; \theta_{y}\right)$：对 Source Domain 进行训练，实现数据的分类任务，本文就是让 Source Domain 的图片分类越正确越好；
  • 域分类器（domain classifier）$G_{d}\left(\cdot ; \theta_{d}\right)$：二分类器，要让 Domain 的分类越正确越好，分类出是 Source 还是 Target ；

　　为什么要加梯度反转层：GRL？

　　域分类器和特征提取器中间有一个梯度反转层（Gradient reversal layer）。梯度反转层顾名思义将梯度乘一个负数，然后进行反向传播。加入GRL的目的是为了让域判别器和特征提取器之间形成一种对抗。

　　最大化 loss $L_{d}$  ，这样就可以尽可能的让两个 domain 分不开， feature 自己就渐渐趋于域自适应了。这是使用 GRL 来实现的，loss $L_{d}$  在 domain classifier 中是很小的，但通过 GRL 后，就实现在 feature extractor 中不能正确的判断出信息来自哪一个域。