P5192 Zoj3229 Shoot the Bullet|东方文花帖|【模板】有源汇上下界最大流

我们要做这道题首先先来学习：

无源汇上下界可行流

什么是无源汇上下界可行流

在一张图中，没有s和t，每条边有流量下界和流量上界，流量在这个区间内，求是否存在一种方案在满足流量平衡的情况下，使所有边满足上下界限制。

先说解法（先接受这种解法再将为什么）：

这是一个网络图（图1）：

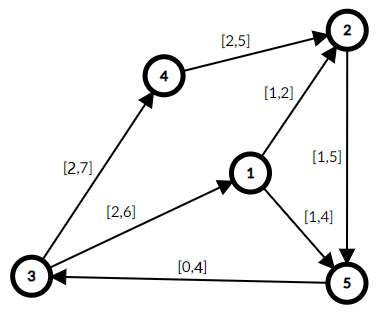
（图1）

以他的每条边的下届为容量再画一个图（图2）

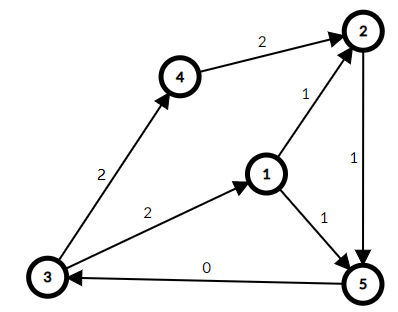
（图2）

在图二上记录每个点为了保持流量平衡，还需要出/入多少流量（这里出/入代表还要出/入多少才可以保证流量平衡（入=出））

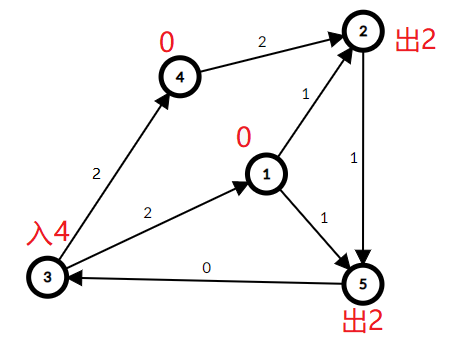
（图2）

在根据他每条边上届减去下届的为容量再画一个图（图3）：

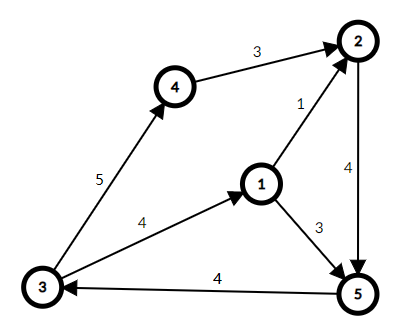
（图3）

将图4跑一边最大流，如果S的出边和T的入边都是满流（流量=容量），则有解。图4跑完最大流的流量+图二每个边的流量就是一种可行流（不算虚点的）（黑色是容量，红色是实际流量）

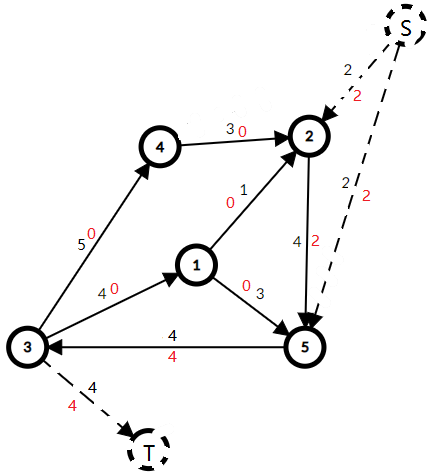
（图4）

下面就是可行流的结果

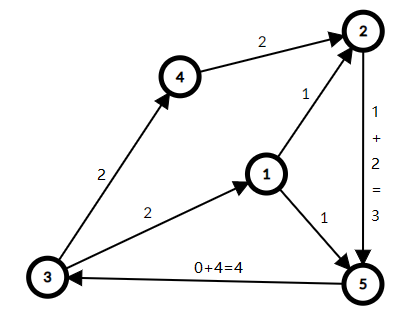
为什么这样是正确的呢？

正确性理解

图2是我们可行流最小的限度，那么可行流一定是在图2（最小流）加上一些值使他流量平衡，这个值肯定是在图3（上下界差）中得出的。

那么这个值到底怎么算出来的呢

首先我们记录了每个点还需要出/入多少流量才能保持流量平衡，如图：

先看点③，还需要流入4的流量才能保持平衡，那么这4的流量一定从别的地方流入，我们让③和T连接一条容量为4的边，并且必须满流（流量也等于4），相当于③必须向T流4的流量，这4的流量必须从别的地方流向③，那么去除虚点后就可以保证有4的流量会流入③，这样图4（差值图/还可以加的图）就抵消了③在图2（最小届）还需要入4的条件。

接着看②，还需要流出2的流量才能保持平衡，那么这2的流量一定从别的地方流出，我们让S和②连接一条容量为2的边，并且必须满流（流量也等于2），相当于S必须向②流2的流量，这2的流量必须向别的地方流出②，那么去除虚点后就可以保证有2的流量会流出②，这样图4（差值图/还可以加的图）就抵消了②在图2（最小届）还需要出2的条件。

点⑤也是同理的哦喵喵~

上面的过程也同时解决了为什么要满流和为什么要跑最大流（最大流可以尽可能保证S，T流出流入的量最多，也就是保证了尽可能满流）和为什么要图4跑完最大流的流量+图二每个边的流量

有源汇上下界可行流

我们在上面考虑无源汇上下界可行流的时候是保证每个点的入流和出流一样就是可行解，现在加入两个点：S和T，只需要再保证S的出=S的入，T的入=T的出就可以直接把有源汇转换成无源汇，现在S有出边，T有入边，并且S的出流=T的入流（这显而易见），我们只用给T一个出边，S一个入边就可行了。

各位巨稍微想一下就可以秒切这个问题：直接从T向S修一条界限为0-inf（这样可以取任何值）的边就可以了

有源汇上下界最大流

搞出可行流，怎么搞最大流呢？

这是作者手胡的一个图：

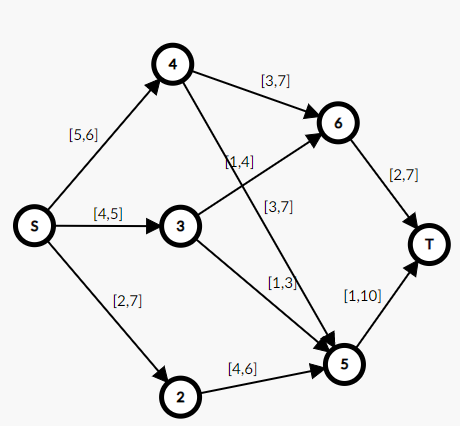
首先我们再来看看我们的可行流

假设我们跑出来的这是可行流（作者也不知道根据上述方法跑出来可行流是什么，先假设是这个）

ans1=我们建的那个t-s的虚边的val（也就是s-t的流量）

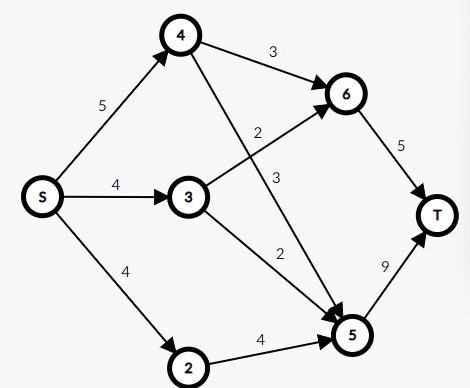
我们用最大界限减去这个可行流，在这个剪出来的图上跑一次最大流ans2：

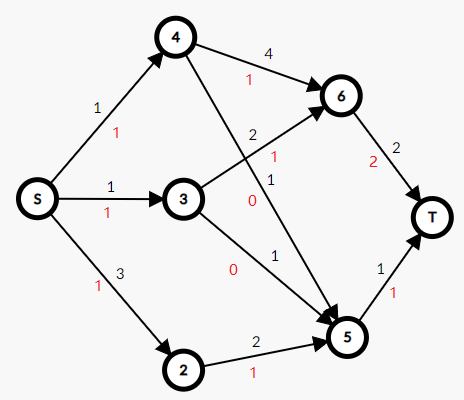
最大流方案就是把这个红色的val和可行流的val加起来

如果只求一个最后最大流把ans1、ans2加起来就是最后的答案啦！

学会了模板，那么我们接下来来分析题目~~

题目分析

“第x个少女拍摄至少Gx​张照片“则S到少女x建\([G_{x},inf]\)

"在第k天的时候文文有Ck​个取材对象，且对于每个取材对象拍的照片必须在闭区间\([L_{k_i},R_{k_i}]\)"则少女i到天k建\([L_{k_i},R_{k_i}]\)

每天的拍照数量不能超过Di​张",则天i到T建\([0,D_{i}]\)

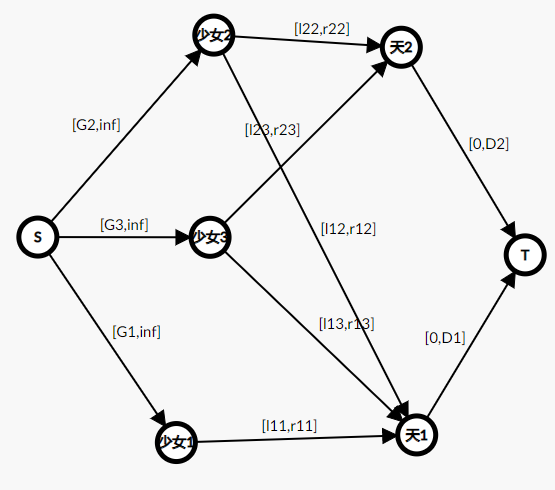
代码细节

看上去有114514张图，其实你只需要建一张图。

那如何算每个点在图2（最下界图）需要再出/入多少呢?(add函数的2,3行就是解决方法)

这是前向星记录的东西(该记的都记)：

这是input函数，注意每次add之前的chu[]++,ru[]++,可以直接算

下面是点的下标

`

s点为1
少女点为2--m+1
天点为m+2--m+n+1
t点为m+n+2
虚拟s为0,虚拟t为m+n+3

`

void input(){
    s=1;t=m+n+2;
    x_s=0;x_t=m+n+3;
    for(int i=1;i<=m;i++){
        scanf("%d",&g);
        ru[i+1]+=g;
        chu[s]+=g;
        add(s,i+1,g,inf);
        add(i+1,s,0,0);
        //add(s,i+1,g,inf);
    }
    for(int i=1;i<=n;i++){
        scanf("%d%d",&c,&d);
        ru[t]+=0;
        chu[i+m+1]+=0;
        add(i+m+1,t,0,d);
        add(t,i+m+1,0,0);
        for(int j=1;j<=c;j++){
            scanf("%d%d%d",&num,&l,&r);
            ru[i+m+1]+=l;
            chu[num+2]+=l;
            add(num+2,i+m+1,l,r);
            add(i+m+1,num+2,0,0);
        }
    }
}

下面是建虚边

void op1(){//建虚边
    for(int i=1;i<=m+n+2;i++){//出入的差距向ST建
        if(chu[i]>ru[i]){
            add(i,x_t,0,chu[i]-ru[i]);
            add(x_t,i,0,0);
        }else if(chu[i]<ru[i]){
            add(x_s,i,0,ru[i]-chu[i]);
            add(i,x_s,0,0);
        }
    }
    add(t,s,0,inf);//TS直接修[0,inf]
    add(s,t,0,0);
}

上文”最大界限减去这个可行流，在这个剪出来的图上跑一次最大流“这个图怎么得到呢？

其实直接把这些虚边删去，然后从原本s-t跑一次最大流就可以得到ans2

为什么呢？其实最大流-这个可行流=r-(l+在有虚ST通过delta跑最大流)=delta-在有虚ST通过delta跑最大流=在第一次跑完最大流（用dinic或者EK或者其他什么高级算法）delta已经减过了在有虚ST通过delta跑最大流，所以可以直接删去虚点跑最大流。

删去虚点虚边代码：

`

void delet(){
    for(int i=head[x_s];i;i=edge[i].next){
        edge[i].l=0;
        edge[i].r=0;
        edge[i].delta=0;
        edge[i^1].l=0;
        edge[i^1].r=0;
        edge[i^1].delta=0;
    }
    for(int i=head[x_t];i;i=edge[i].next){
        edge[i].l=0;
        edge[i].r=0;
        edge[i].delta=0;
        edge[i^1].l=0;
        edge[i^1].r=0;
        edge[i^1].delta=0;
    }
    edge[tot].l=0;//tot代表最后一次建的边也就是t-s那个虚边
    edge[tot].r=0;
    edge[tot].delta=0;
    edge[tot^1].l=0;
    edge[tot^1].r=0;
    edge[tot^1].delta=0;
    x_s=s;
    x_t=t;
} `

这是判断是否满流：

`

bool pd(){
    for(int i=head[x_s];i;i=edge[i].next){
        if(edge[i].delta!=0){
            return 0;
        }
    }
    return 1;
}`

总代码

`

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10,inf=1e9+7;
int n,m,s,t,g,c,d;//实际st
int x_s,x_t,tot=1,head[N],l,r,num;//虚拟st
int ru[N],chu[N],de[N],now[N],vis[N],bj;
int ans1=0,ans2;
queue<int>q;
//s点为1
//少女点为2--m+1
//天点为m+2--m+n+1
//t点为m+n+2
//虚拟s为0,t为m+n+3
struct node{
    int from,next,to,l,r,delta;
}edge[2*N];
void add(int x,int y,int l,int r){
    tot++;
    edge[tot].from=x;
    edge[tot].to=y;
    edge[tot].l=l;
    edge[tot].r=r;
    edge[tot].delta=r-l;
    edge[tot].next=head[x];
    head[x]=tot;
}
void input(){
    s=1;t=m+n+2;
    x_s=0;x_t=m+n+3;
    for(int i=1;i<=m;i++){
        scanf("%d",&g);
        ru[i+1]+=g;
        chu[s]+=g;
        add(s,i+1,g,inf);
        add(i+1,s,0,0);
        //add(s,i+1,g,inf);
    }
    for(int i=1;i<=n;i++){
        scanf("%d%d",&c,&d);
        ru[t]+=0;
        chu[i+m+1]+=0;
        add(i+m+1,t,0,d);
        add(t,i+m+1,0,0);
        for(int j=1;j<=c;j++){
            scanf("%d%d%d",&num,&l,&r);
            ru[i+m+1]+=l;
            chu[num+2]+=l;
            add(num+2,i+m+1,l,r);
            add(i+m+1,num+2,0,0);
        }
    }
}
bool bfs(){//分层
    memset(de,127,sizeof(de));
    q.push(x_s);
    de[x_s]=1;
    vis[x_s]=1;
    while(!q.empty()){
        int x=q.front();
        q.pop();
        vis[x]=0;
        for(int i=head[x];i;i=edge[i].next){
            int y=edge[i].to;
            if(de[y]>de[x]+1&&edge[i].delta){
                de[y]=de[x]+1;
                if(vis[y]==0){
                    q.push(y);
                }
            }
        }
    }
    if(de[x_t]<inf) return 1;
    return 0;
}
int dfs(int x,int ans){
    int rest=ans;
    if(x==x_t) return ans;
    vis[x]=1;
    for(int i=now[x];i&&rest;i=edge[i].next){
        int y=edge[i].to;
        now[x]=i;
        if(de[y]==de[x]+1&&!vis[y]&&edge[i].delta!=0){
            int k=dfs(y,min(rest,edge[i].delta));
            if(k){
                edge[i].delta-=k;
                edge[i^1].delta+=k;
                rest-=k;
            }
        }
    }
    vis[x]=0;
    return ans-rest;
}
void op1(){//在区间最小的时候跑一下出和入
    for(int i=1;i<=m+n+2;i++){
        if(chu[i]>ru[i]){
            add(i,x_t,0,chu[i]-ru[i]);
            add(x_t,i,0,0);
        }else if(chu[i]<ru[i]){
            add(x_s,i,0,ru[i]-chu[i]);
            add(i,x_s,0,0);
        }
    }
    add(t,s,0,inf);
    add(s,t,0,0);
}
void op2(){//用新建的和delta跑最大流
    while(bfs()){
//        for(int i=0;i<=n+m+3;i++) printf("%d",de[i]);
//        cout<<endl;
        for(int i=0;i<=n+m+3;i++) now[i]=head[i];
        ans1+=dfs(x_s,inf);
    }
}
void delet(){
    for(int i=head[x_s];i;i=edge[i].next){
        edge[i].l=0;
        edge[i].r=0;
        edge[i].delta=0;
        edge[i^1].l=0;
        edge[i^1].r=0;
        edge[i^1].delta=0;
    }
    for(int i=head[x_t];i;i=edge[i].next){
        edge[i].l=0;
        edge[i].r=0;
        edge[i].delta=0;
        edge[i^1].l=0;
        edge[i^1].r=0;
        edge[i^1].delta=0;
    }
    edge[tot].l=0;
    edge[tot].r=0;
    edge[tot].delta=0;
    edge[tot^1].l=0;
    edge[tot^1].r=0;
    edge[tot^1].delta=0;
    x_s=s;
    x_t=t;
}
bool pd(){
    for(int i=head[x_s];i;i=edge[i].next){
        if(edge[i].delta!=0){
            return 0;
        }
    }
    return 1;
}
int main(){
    while(cin>>n>>m){
        bj=0;
        memset(head,0,sizeof(head));
        memset(edge,0,sizeof(edge));
        memset(chu,0,sizeof(chu));
        memset(ru,0,sizeof(ru));
        input();
        op1();
        op2();
        if(!pd()){
            printf("-1\n\n");
            continue;
        }
        ans2=edge[tot].delta;
        ans1=0;
        delet();
        op2();
        printf("%d\n\n",ans1+ans2);
    }

    return 0;
}`

完结撒花~~~~