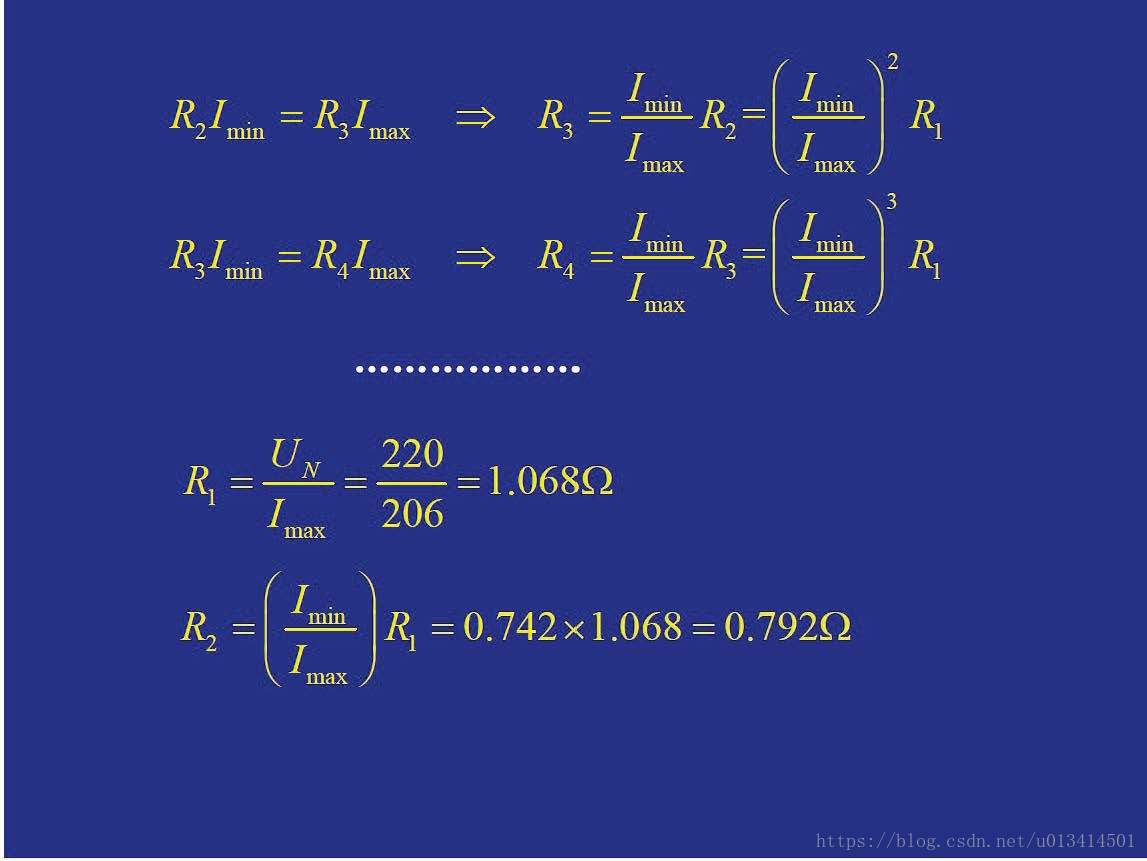模型预测控制(MPC)简介
1.引言
在当今过程控制中,PID当然是用的最多的控制方法,但MPC也超过了10%的占有率。MPC是一个总称,有着各种各样的算法。其动态矩阵控制(DMC)是代表作。DMC采用的是系统的阶跃响应曲线,其突出的特点是解决了约束控制问题。那么是DMC是怎么解决约束的呢?在这里只给出宏观的解释,而不做详细的说明。DMC把线性规划和控制问题结合起来,用线性规划解决输出约束的问题,同时解决了静态最优的问题,一石二鸟,在工业界取得了极大的成功。
2.作用机理
MPC作用机理描述为:在每一个采用时刻,根据获得的当前测量信息,在线求解一个有限时间开环优化问题,并将得到的控制序列的第一个元素作用于被控对象。在下一个采样时刻,重复上述过程:用新的测量值作为此时预测系统未来动态的初始条件,刷新优化问题并重新求解 。
即MPC算法包括三个步骤:
(1)预测系统未来动态;
(2)(数值)求解开环优化问题;
(3)将优化解的第一个元素(或者说第一部分)作用于系统
这三步是在每个采样时刻重复进行的,且无论采用什么样的模型,每个采样时刻得到的测量值都作为当前时刻预测系统未来动态的初始条件
在线求解开环优化问题获得开环优化序列是MPC和传统控制方法的主要区别,因为后者通常是离线求解一个反馈控制律,并将得到的反馈控制律一直作用于系统。
在这里给出两点说明:
1.MPC是一个反馈控制策略,但是之前不是说将得到的控制序列中的第一个元素作用于被控对象,求解开环问题。那么哪来的反馈呢?
实际上在下一个采样周期,下一时刻的测量值又被使用上了,用下一时刻的测量值求解下一时刻的控制值。故这是一个反馈控制策略
2.传统的控制方法为什么被称为离线控制?
举例说明:
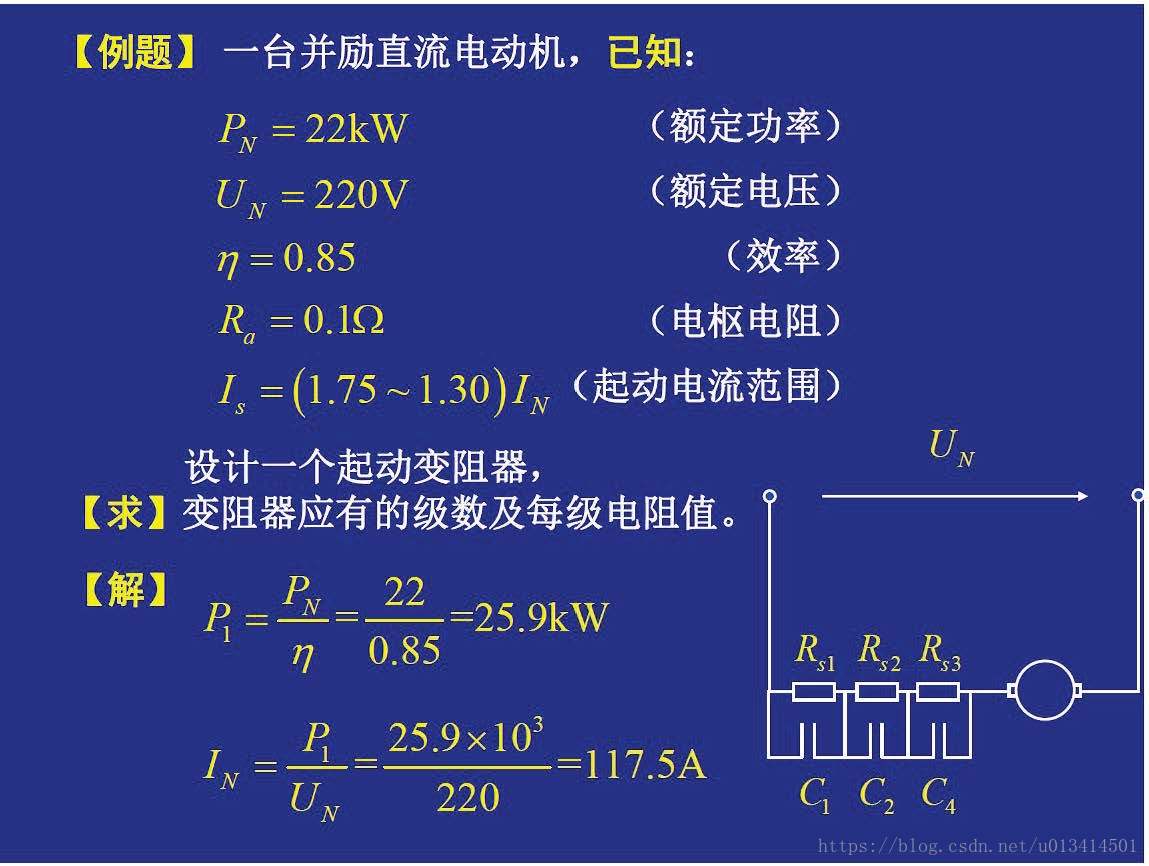
上面几张图片是设计变阻器应有的级数来达到控制并励直流电动机启动的例子,那么如何看的出来是离线控制呢?其实很简单,在起始的时候就已经把每级电阻值就给定出来了,但是实际上是否能如理论计算的这样呢?比如我电压突然受到了扰动了怎么办?那么这个计算的每级电阻值肯定不对了啦,但是传统的控制方法对此确是无能为力的,因为每级启动电阻在最早的时候已经计算好了的。
3.MPC的基本特点
不管是何种算法,他们的基本特点都是:基于模型的预测、滚动优化和前馈-反馈的控制结构。
1.基于模型的预测
在MPC算法中,需要一个描述对象动态行为的模型,这个模型的作用是预测系统未来的动态。即能够根据系统k时刻的状态和k时刻的控制输入,预测到k+1时刻的输出。在这里k时刻的输入正是用来控制系统k+1时间的输出,使其最大限度的接近k+1时刻的期望值。故我们强调的是该模型的预测作用,而不是模型的形式。
在这里我重点讲解一下状态空间模型。那么什么是状态?输出是不是也是状态的一种?
对的,输出也是一种状态,只不过我们赋予了这个状态特殊的意义。举个例子来说,舞龙,假设是只能通过龙尾的人A指挥前面一个人B动作,然后B指挥他前面的一个人C动作….依次如此,达到控制龙头的人F叼住绣球的动作。如果只关注龙头的人(输出)和龙尾的人(输入),而忽略龙身子的动态,那就是所谓的输入—输出系统。经典控制理论就是建立在输入—输出系统的基础上面的。 但是我如果不管要管龙尾和龙头的人,我连龙身子上面的人也要要求在固定的位置,那么这就是状态空间的概念,即我对系统中的每一个状态都要控制到。龙头位置的人也是一个状态,故输出本身就是一个状态,或者说是状态的一个组合。
这里可以将经典控制理论中的微分方程/传递函数做对比
微分方程/传递函数所描绘是输入输出的转态情况,即上面所说的龙头和龙尾的状态变化
现代控制理论中的状态空间模型,所描绘的是系统中所有状态量之间的变化情况,即上面所说的龙头、龙尾以及之间的每个节点(人)的状态变化。
2.滚动优化
因为外部干扰和模型失配的影响,系统的预测输出和实际输出存在着偏差,如果测量值能测到这个偏差,那么在下一时刻能根据这个测量到偏差的测量值在线求解下一时刻的控制输入,即优化掉了这个偏差值。若将求解的控制输出的全部序列作用于系统,那么k+1时刻的测量值不能影响控制动作,也就是说测量值所包括的外部干扰或模型误差信息得不到有效利用。故我们将每个采样时刻的优化解的第一个分量作用于系统,在下一个采用时刻,根据新得到的测量值为初始条件重新预测系统的未来输出并求解优化解,继续将这个时刻的优化解的第一个分量作用于系统,这样重复至无穷。
故预测控制不是采用一个不变的全局优化目标,而是采用时间向前滚动式的有限时域优化策略。这也就是意味着优化过程不是一次离线进行,而是反复在线进行的。
3.前馈-反馈的控制结构
这个在前面给出的两点说明中的第一点就已经给出了。
实际上在下一个采样周期,此这一时刻测量值又被使用上了,用这一时刻的测量值求解这一时刻的控制值。故这是一个反馈控制策略
模型预测控制(MPC)简介的更多相关文章
- 【控制】模型预测控制 MPC 【合集】Model Predictive Control
1.模型预测控制--运动学模型 2.模型预测控制--模型线性化 3.模型预测控制--模型离散化 4.模型预测控制--预测 5.模型预测控制--控制律优化二次型优化 6.模型预测控制--反馈控制 7.模 ...
- 模型预测控制 MPC
使用MPC的原因:
- MATLAB模型预测控制(MPC,Model Predictive Control)
模型预测控制是一种基于模型的闭环优化控制策略. 预测控制算法的三要素:内部(预测)模型.参考轨迹.控制算法.现在一般则更清楚地表述为内部(预测)模型.滚动优化.反馈控制. 大量的预测控制权威性文献都无 ...
- 无人驾驶——4.控制之MPC模型预测控制
源自:<无人驾驶无人驾驶车辆模型预测控制>——龚建伟 参考:https://wenku.baidu.com/view/8e4633d519e8b8f67c1cb9fa.html 0.车辆模 ...
- 一个模型预测控制(MPC)的简单实现
1 生活中的启示 情景如下:你们团队每天早晨开一次例会,主要会议内容是你汇报工作进度,领导根据工作目标和工作进度,制定当天的工作计划,你领到工作计划后开始工作.每天都这样周而复始,从领导的角度看,这件 ...
- python 全栈开发,Day70(模板自定义标签和过滤器,模板继承 (extend),Django的模型层-ORM简介)
昨日内容回顾 视图函数: request对象 request.path 请求路径 request.GET GET请求数据 QueryDict {} request.POST POST请求数据 Quer ...
- Django基础(2)--模板自定义标签和过滤器,模板继承 (extend),Django的模型层-ORM简介
没整理完 昨日回顾: 视图函数: request对象 request.path 请求路径 request.GET GET请求数据 QueryDict {} request.POST POST请求数据 ...
- 基本I/O模型与Epoll简介
5种基本的I/O模型:1)阻塞I/O ;2)非阻塞I/O; 3)I/O复用(select和poll);4)信号驱动I/O(SIGIO);5)异步I/O(POSIX.1的aio_系列函数). 操作系统中 ...
- Apollo代码学习(七)—MPC与LQR比较
前言 Apollo中用到了PID.MPC和LQR三种控制器,其中,MPC和LQR控制器在状态方程的形式.状态变量的形式.目标函数的形式等有诸多相似之处,因此结合自己目前了解到的信息,将两者进行一定的比 ...
随机推荐
- weblogic自动化打补丁脚本
转至:https://www.it610.com/article/1294086996750311424.htm 目的 weblogic每个季度都会有psu更新,打补丁操作也变成了每个季度都要做的事情 ...
- redis数据类型的使用及介绍
Redis数据类型 1.Sting类型 set命令 设置键值,存在则覆盖,不存在则新建 set key value EX 秒 设置有效时长为秒 nx 如果键不存在则新建,如果存在返回nil xx 只有 ...
- Flutter ChartSpace:通过跨端 Canvas 实现图表库
基于Flutter 的图形语法库,通过跨端 Canvas ,将基于 Javascript 的图形语法库 ChartSpace 扩展至 Flutter 端 作者:字节跳动终端技术--胡珀 背景 数据平台 ...
- jQuery Validatede 结合Ajax 表单验证提交
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- vant list列表滚动到底部加载更多会滚动到顶部问题
如果使用异步加载数据并使用了vant中的toast做加载中提示,则有可能会导致列表滚动高度为0,也就是回到了顶部.只要在list加载回调里不使用toast就可以避免这个问题.
- VuePress 博客之 SEO 优化(三)标题、链接优化
前言 在 <一篇带你用 VuePress + Github Pages 搭建博客>中,我们使用 VuePress 搭建了一个博客,最终的效果查看:TypeScript 中文文档. 本篇讲讲 ...
- freeswitch tts_commandline模块介绍
概述 freeswitch是开源.免费的VOIP软交换平台,自带了很多功能各异的模块. mod_tts_commandline模块,本身没有TTS能力,而是通过调用TTS引擎的命令生成语音文件,tts ...
- ArcMap操作随记(11)
1.直方图 在[Spatial Analyst]工具条中 2.分辨率变换 [重采样] :①最近邻法 ②双线性 ③三次卷积 重采样过程中要注意Nodata值 3.用ArcGIS进行监督分类 [影像分类] ...
- kubernetes证书过期处理
rancher中文文档:http://docs.rancher.cn/ k8s中文文档:https://kubernetes.io/zh/docs 一.修改kubeadm 源码 增加证书到100年 $ ...
- MySQL知识补充(表字段操作、视图、触发器、事物、存储过程、内置函数、流程控制、索引、慢查询)
今日内容概要 表字段操作补充(掌握) 视图(了解) 触发器(了解) 事务(掌握) 存储过程(了解) 内置函数(了解) 流程控制(了解) 索引(熟悉) 内容详细 1.表字段操作补充 # 1.添加表字段 ...