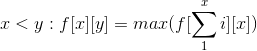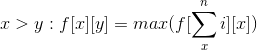弹簧高跷题解---双向DP---DD(XYX)的博客
三 . 弹簧高跷
时间限制: 1 Sec 内存限制: 128 MB
题目描述、输入、输出
-----------
方法
这道题用DP是可以解决的。因为每一次跳跃都与前一次跳跃有关,也就是说,每次要枚举前两次的跳跃落点,然后才能计算出某点到一个落点的最优解。这样一来,就可以定义一个 f [ ] [ ] ,f[ i ][ j ] 表示 以 “ 从 i 点跳到 j 点 ” 结束 的 一整次跳跃过程 中,得到的最高分 (注意: 可能是 i < j,也可能是 i > j,当然也有 i = j 的情况)。状态转移方程:
(分数)
先处理 f[ i ][ i ] 的情况,然后正逆序都进行一次三重循环。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
void read(int &x) {
int f = 1;x = 0;char s = getchar();
while(s < '0' || s > '9') {if(s == '-')f = -1;s = getchar();}
while(s >= '0' && s <= '9') {x = x * 10 + s - '0';s = getchar();}
x *= f;
}
struct no{
int x,h;
}a[1005];
bool operator < (no a,no b) {
return a.x < b.x;
}
bool operator > (no a,no b) {
return b < a;
}
int n,m,s,o,i,j,k,ans = 0;
int dp[1005][1005];
int main() {
read(n);
for(i = 1;i <= n;i ++) {
read(a[i].x);read(a[i].h);
ans = max(ans,a[i].h);
}
sort(a + 1,a + 1 + n);
for(i = 1;i <= n;i ++) {
dp[i][i] = a[i].h;
for(j = 1;j < i;j ++) {
dp[j][i] = dp[j][j];
for(k = j - 1;k > 0 && a[j].x - a[k].x <= a[i].x - a[j].x;k --) {
dp[j][i] = max(dp[j][i],dp[k][j]);
}
dp[j][i] += a[i].h;
ans = max(ans,dp[j][i]);
}
}
for(i = n;i > 0;i --) {
for(j = n;j > i;j --) {
dp[j][i] = dp[j][j];
for(k = j + 1;k <= n && a[k].x - a[j].x <= a[j].x - a[i].x;k ++) {
dp[j][i] = max(dp[j][i],dp[k][j]);
}
dp[j][i] += a[i].h;
ans = max(ans,dp[j][i]);
}
}
printf("%d",ans);
return 0;
}
弹簧高跷题解---双向DP---DD(XYX)的博客的更多相关文章
- (四连测)滑雪场的高度差题解---二分 + 搜索---DD(XYX)的博客
滑雪场的高度差 时间限制: 1 Sec 内存限制: 128 MB 题目描述 滑雪场可以看成M x N的网格状山地(1 <= M,N <= 500),每个网格是一个近似的平面,具有水平高度 ...
- 圆形谷仓Circular Barn_Silver---(DP优化 / )队列 + 贪心(复杂度O(2n))---DD(XYX)的博客
目录 小数据 大数据 小数据 题目描述 农夫约翰有一个圆形的谷仓,谷仓分成了环形的n(3≤n≤1000)个房间,编号为1 , 2 , -- .每个房间有三个门,两个门通往两个相邻的房间,第三个门朝外. ...
- 拥挤的奶牛题解---队列优化DP---DD(XYX)的博客
拥挤的奶牛 时间限制: 1 Sec 内存限制: 128 MB 题目描述 FJ的n头奶牛(1<=n<=50000)在被放养在一维的牧场.第i头奶牛站在位置x(i),并且x(i)处有一个高度 ...
- 你有PSD的学位吗? - dp的日志 - 网易博客
你有PSD的学位吗? - dp的日志 - 网易博客 你有PSD的学位吗? 2011-08-01 12:58:40| 分类: 感悟 | 标签:自我提升 |字号 大中小 订阅 去年, ...
- 洛谷P2507 [SCOI2008]配对 题解(dp+贪心)
洛谷P2507 [SCOI2008]配对 题解(dp+贪心) 标签:题解 阅读体验:https://zybuluo.com/Junlier/note/1299251 链接题目地址:洛谷P2507 [S ...
- Blocks题解(区间dp)
Blocks题解 区间dp 阅读体验...https://zybuluo.com/Junlier/note/1289712 很好的一道区间dp的题目(别问我怎么想到的) dp状态 其实这个题最难的地方 ...
- POJ-2282题解&数位DP总结
一.题意 给定一个区间[a, b](注意输入的时候可能a > b,所以,在数据输入后,要先比较a和b,如果a > b,交换a和b的值),统计这个区间里面,数位上有多少个0.多少个1.--. ...
- HDU3085NightmareII题解--双向BFS
题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=3085 分析 大意就是一个男孩和一个女孩在网格里,同时还有两个鬼,男孩每轮走三步,女孩每轮走一步,与鬼曼 ...
- HDU4507 吉哥系列故事——恨7不成妻 题解 数位DP
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4507 题目大意: 找到区间 \([L,R]\) 范围内所有满足如下条件的数的 平方和 : 不包含'7' ...
随机推荐
- SpringCloudAlibaba分布式流量控制组件Sentinel实战与源码分析(上)
概述 定义 Sentinel官网地址 https://sentinelguard.io/zh-cn/index.html 最新版本v1.8.4 Sentinel官网文档地址 https://senti ...
- Linux(Centos7)静默安装Oracle19C
Oracle数据库服务器一般都是Linux,Linux服务器一般都是在非图形界面的操作,本文章手把手教你如何在非图形界面安装Oracle19C. ORACLE 19C 的安装包自行在官网下载,下载免费 ...
- C#中常用的目录|文件|路径信息操作
更新记录 本文迁移自Panda666原博客,原发布时间:2021年5月16日. 说明 .NET的类库API设计的非常优秀,再加上文档docs.com写的非常优秀,写代码给人一种十分优雅的感觉. 获得当 ...
- 解决maven依赖冲突,这篇就够了!
一.前言 什么是依赖冲突 依赖冲突是指项目依赖的某一个jar包,有多个不同的版本,因而造成了包版本冲突. 依赖冲突的原因 我们在maven项目的pom中 一般会引用许许多多的dependency.例如 ...
- vue大型电商项目尚品汇(后台篇)day03
今天把平台属性的管理基本完成了,后台管理做到现在基本也开始熟悉,确实就是对ElementUI的一个熟练程度. 一.平台属性管理 1.动态展示数据 先把接口弄好,应该在第三级标题选择后进行发请求 静态页 ...
- 一文get到SOLID原则的重点
最近没事再次翻开<敏捷软件开发:原则.模式与实践>看,发现以前似懂非懂的东西突然就看懂了,get到了讲的重点. SOLID(单一职责原则.开放-封闭原则.里氏替换原则.接口隔离原则以及 ...
- 有关于weiphp2.00611上传sae的一些注意(图片上传解决方案)
一.安装中注意的事项 安装时使用的系统为weiphp2.0611 版本 1.将所有文件上传到代码库中 2.按照步骤进行安装weiphp,注意在数据库导入的时候需要手动导入. ...
- SpringBoot项目集成Swagger启动报错: Failed to start bean 'documentationPluginsBootstrapper'; nested exception is
使用的Swagger版本是2.9.2.knife4j版本是2.0.4. SpringBoot 版本是2.6.2将SpringBoot版本回退到2.5.6就可以正常启动
- AI 绘画极简教程
昨天在朋友圈发了几张我用AI绘画工具Disco Diffusion画的画 既然有同学问,就写个极简教程吧,画个图是足够了,想要深入了解还是自行百度吧,可以找到更详细的教程. 第 0 步:学会上网,注册 ...
- C++ 练气期之二维数组与矩阵运算
1. 前言 C++中的一维数组可以存储线性结构的数据,二维数组可以存储平面结构的数据.如班上所有学生的各科目成绩就有二个维度,学生姓名维度和科目成绩维度. 这样的表格数据可以使用二维数组进行存储. 当 ...