Graph Theory の brief introduction

一. 图的概念

  1.定义

  某类具体事物（顶点）和这些事物之间的联系（边）,由顶点（vertex）和边（edge）组成, 顶点的集合V，边的集合E，图记为G = (V,E)

2.分类

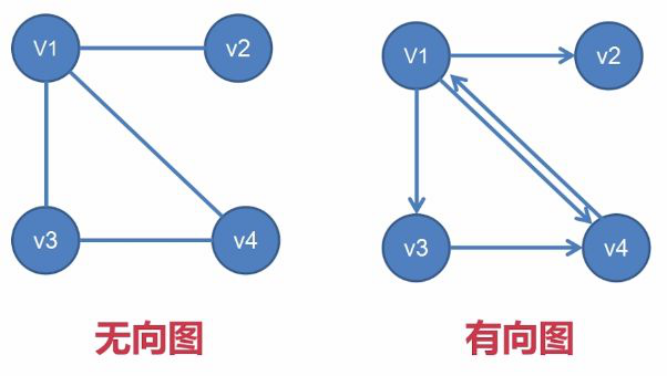
    1、无向图 Def：边没有指定方向的图

    2、有向图 Def：边具有指定方向的图 （有向图中的边又称为弧，起点称为弧头，终点称为 弧尾）

    3.带权图 Def: 边上带有权值的图。（不同问题中，权值意义不同，可以是距离、时间、价格、代价等不同属性）

3.无向图的术语

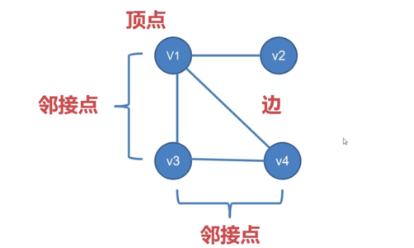
 两个顶点之间如果有边连接，那么就视为两个顶点相邻。

 路径：相邻顶点的序列。

 圈：起点和终点重合的路径。

 连通图：任意两点之间都有路径连接的图。

 度：顶点连接的边数叫做这个顶点的度。

树：没有圈的连通图。

 森林：没有圈的非连通图。

                  连通图                   非连通图

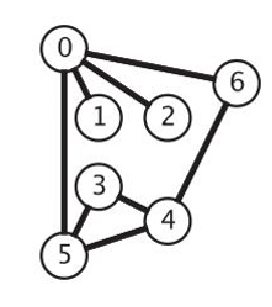
4.有向图的术语

在有向图中，边是单向的：每条边所连接的两个顶点是一个有序对，他们的邻接性是单向的。

有向路径：相邻顶点的序列。

有向环：一条至少含有一条边且起点和终点相同的有向路径。

有向无环图（DAG）：没有环的有向图。

度：一个顶点的入度与出度之和称为该顶点的度。

  1）入度：以顶点为弧头的边的数目称为该顶点的入度

  2）出度：以顶点为弧尾的边的数目称为该顶点的出度

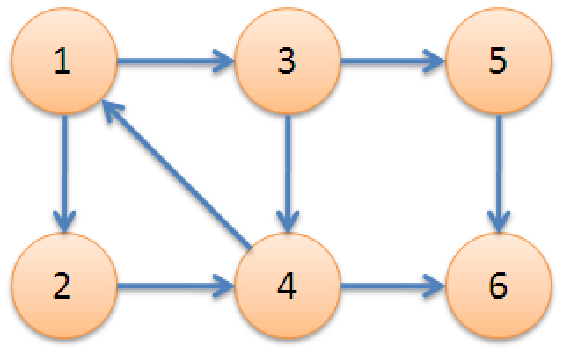
eg.

1->3->5->6 ：有向路径      1->3->4->1 ：有向环      (3、4、5、6) ：无环有向图

节点1的度：3     节点1的入度：1     节点1的出度：2

二.图的表示

  引入：如何用计算机来存储图的信息（顶点、边），这是图的存储结构要解决的问题？

 1、邻接矩阵

  对于一个有V的顶点的图而言，可以使用V*V的二维数组表示。G[i][j] 表示的是顶点i与顶点j的关系。

    如果顶点i和顶点j之间 有边相连， G[i][j]=1

    如果顶点i和顶点j之间 无边相连， G[i][j]=0

  对于无向图：G[i][j]=G[j][i]

  在带权图中，如果在边不存在的情况下，将G[i][j]设置为0，则无法与权值为0的情况分开，因此选择较大的常数INF即可。

  邻接矩阵的优点：可以在常数时间内判断两点之间是否有边存在。

    邻接矩阵的缺点：表示稀疏图时，浪费大量内存空间。表示稠密图还是很划算。

  

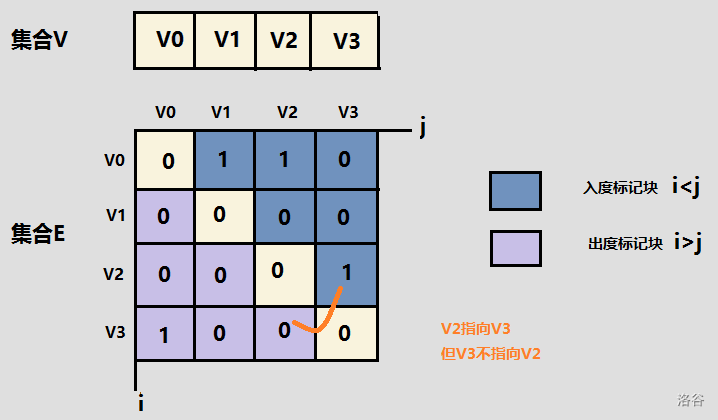
  eg. 邻接矩阵存储图

Code

 #include<bits/stdc++.h>
using namespace std;
int a[1005][1005];
int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	int u,v;
	for(int i=1;i<=m;i++){
		scanf("%d%d",&u,&v);
		a[u][v]=a[v][u]=1;
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(a[i][j])
				printf("%d ",j);
		}
		printf("\n");
	}
	return 0;
}

 2、邻接表

  通过把“从顶点0出发有到顶点2，3，5的边”这样的信息保存在链表中来表示图。

  

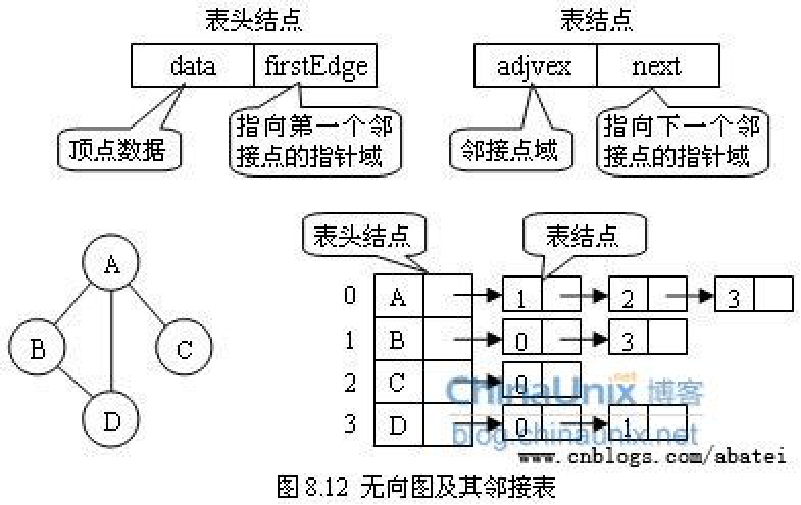
出边表的表结点存放的是从表头结点出发的有向边所指的尾顶点

入边表的表结点存放的则是指向表头结点的某个头顶点

 带权图的邻接表  :在表结点中增加一个存放权的字段 

  

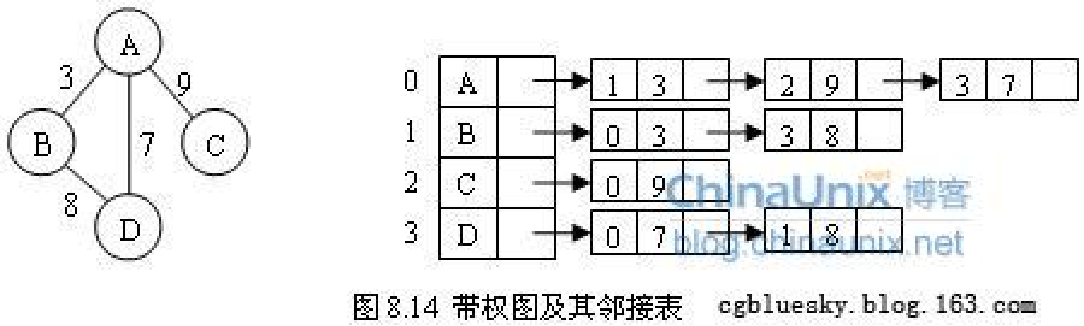
eg.

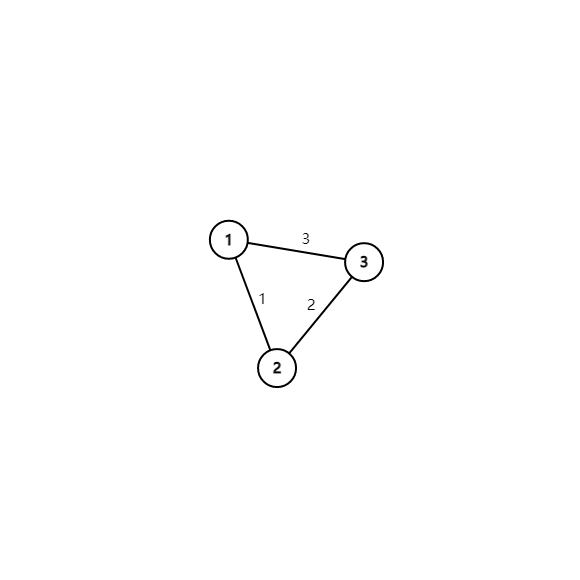
将如下的图利用邻接表进行表示，并输出每个顶点的度。 

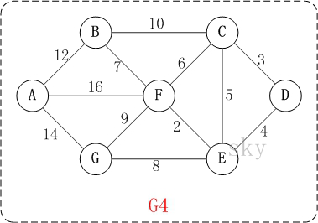
Code

 #include<vector>
//存边（编号和边权）
struct edge{
	int v,w;
	edge(){}
	//构造函数
	edge(int V,int W){
		v=V;
		w=W;
	}
};
vector<edge> G[maxn];

void addEdge(int u,int v,int w){
	G[u].push_back(edge(v,w));
}

for(int i=1;i<=N;++i){
	int u,v,w;
	cin>>u>>v>>w;
	addEdge(u,v,w);
	addEdge(v,u,w);
}

 3.链式前向星

  参考：链式前向星--最通俗易懂的讲解

如果说邻接表是不好写但效率好，邻接矩阵是好写但效率低的话，前向星就是一个相对中庸的数据结构。前向星固然好写，但效率并不高。而在优化为链式前向星后，效率也得到了较大的提升。虽然说，世界上对链式前向星的使用并不是很广泛，但在不愿意写复杂的邻接表的情况下，链式前向星也是一个很优秀的数据结构。                                                                                                                                                                  ——摘自《百度百科》

链式前向星其实就是静态建立的邻接表，时间效率为O（m），空间效率也为O（m）。遍历效率也为O（m）。

对于下面的数据，第一行5个顶点，7条边。接下来是边的起点，终点和权值。也就是边1 -> 2 权值为1。

样例

 5 7
1 2 1
2 3 2
3 4 3
1 3 4
4 1 5
1 5 6

链式前向星存的是以【1，n】为起点的边的集合，对于上面的数据输出就是：

print

 1 //以1为起点的边的集合
1 5 6
1 3 4
1 2 1

2 //以2为起点的边的集合
2 3 2

3 //以3为起点的边的集合
3 4 3

4  //以4为起点的边的集合
4 5 7
4 1 5

5 //以5为起点的边不存在

对比邻接表

 对于邻接表来说是这样的：
1 -> 2 -> 3 -> 5
2 -> 3
3 -> 4
4 -> 1 -> 5
5 -> ^
对于链式前向星来说是这样的：
edge[0].to = 2; edge[0].next = -1; head[1] = 0;
edge[1].to = 3; edge[1].next = -1; head[2] = 1;
edge[2].to = 4; edge[2],next = -1; head[3] = 2;
edge[3].to = 3; edge[3].next = 0; head[1] = 3;
edge[4].to = 1; edge[4].next = -1; head[4] = 4;
edge[5].to = 5; edge[5].next = 3; head[1] = 5;
edge[6].to = 5; edge[6].next = 4; head[4] = 6;
简化后：1 -> 5 -> 3 -> 2

  由此可见对于每一个节点，输出的顺序为输入时的逆序

我们先对上面的7条边进行编号第一条边是0以此类推编号【0~6】，然后我们要知道两个变量的含义：

• Next ：表示与这个边起点相同的上一条边的编号。
• head[ i ] ：数组，表示以 i 为起点的最后一条边的编号。

  加边函数是这样的：

void add_edge(int u, int v, int w)//加边，u起点，v终点，w边权
{
    edge[cnt].to = v; //终点
    edge[cnt].w = w; //权值
    edge[cnt].next = head[u];//以u为起点上一条边的编号，也就是与这个边起点相同的上一条边的编号
    head[u] = cnt++;//更新以u为起点上一条边的编号
}

  遍历函数是这样的：

for(int i = 1; i <= n; i++)//n个起点
    {
        cout << i << endl;
        for(int j = head[i]; j != -1; j = edge[j].next)//遍历以i为起点的边
        {
            cout << i << " " << edge[j].to << " " << edge[j].w << endl;
        }
        cout << endl;
    }

第一层for循环是找每一个点，依次遍历以【1，n】为起点的边的集合。第二层for循环是遍历以 i 为起点的所有边，k首先等于head[ i ]，注意head[ i ]中存的是以 i 为起点的最后一条边的编号。然后通过edge[ j ].next来找下一条边的编号。我们初始化head为-1，所以找到你最后一个边（也就是以 i 为起点的第一条边）时，你的edge[ j ].next为 -1做为终止条件。

Code

 #include<bits/stdc++.h>
using namespace std;
const int maxn = 1005;//点数最大值
int n, m, cnt;//n个点，m条边
struct Edge
{
    int to, w, next;//终点，边权，同起点的上一条边的编号
}edge[maxn];//边集
int head[maxn];//head[i],表示以i为起点的第一条边在边集数组的位置（编号）
void init()//初始化
{
    for (int i = 0; i <= n; i++) head[i] = -1;
    cnt = 0;
}
void add_edge(int u, int v, int w)//加边，u起点，v终点，w边权
{
    edge[cnt].to = v; //终点
    edge[cnt].w = w; //权值
    edge[cnt].next = head[u];//以u为起点上一条边的编号，也就是与这个边起点相同的上一条边的编号
    head[u] = cnt++;//更新以u为起点上一条边的编号
}
int main()
{
    cin >> n >> m;
    int u, v, w;
    init();//初始化
    for (int i = 1; i <= m; i++)//输入m条边
    {
        cin >> u >> v >> w;
        add_edge(u, v, w);//加边
        /*
        加双向边
        add_edge(u, v, w);
        add_edge(v, u, w);
        */
    }
    for (int i = 1; i <= n; i++)//n个起点
    {
        cout << i << endl;
        for (int j = head[i]; j != -1; j = edge[j].next)//遍历以i为起点的边
        {
            cout << i << " " << edge[j].to << " " << edge[j].w << endl;
        }
        cout << endl;
    }
    return 0;
}

三.图的遍历

  从图中的某个顶点出发，按某种方法对图中的所有顶点访问且仅访问一次。为了保证图中的顶点在遍历过程中仅访问一次，要为每一个顶点设置一个访问标志。

  1.DFS

概念

深度优先搜索(Depth-First Search)遍历类似于树的先根遍历，是树的先根遍历的推广。假设初始状态是图中所有顶点未曾被访问，则深度优先搜索可从图中某 个顶点v出发，访问此顶点，然后依次从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到；若此时图中尚有顶点未被访 问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

Code

Code

 #include<bits/stdc++.h>
#define Maxn 205
using namespace std;
int n, m;
bool a[Maxn][Maxn], vis[Maxn];
void DFS(int i) {
    cout << i << ' ';
    vis[i] = 1;
    for (int j = 1; j <= n; j++) {
        if (a[i][j]) {
            if (!vis[j]) {
                vis[j] = 1;
                DFS(j);
            }
        }
    }
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        a[x][y] = 1;
    }
    for (int i = 1; i <= n; i++) {
        if (!vis[i])
            DFS(i);
    }
    return 0;
}

2.BFS

对(a)进行广度优先搜索 遍历的过程如图(b)所示， 得到的顶点访问序列为: v1->v2->v3->v4->v5->v6->v7->v8

       

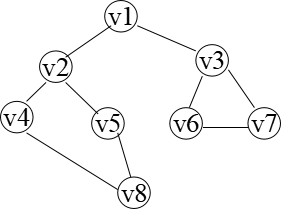
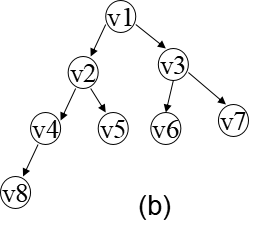
概念

广度优先搜索(Breadth-First Search)遍历类似于树的按层次遍历的过程。 假设从图中某顶点v出发，在访问v之后依次访问v的各个未被访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接 点”先于“后被访问的顶点的邻接点”被访问，直至图中所有已被访问的顶点的邻接点都被访问到。若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的 顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。换句话说，广度优先搜索遍历图的过程是以v为起始点，由近至远，依次访问和v有路径相通 且路径长度为1，2，…的顶点。

Code

 #include<bits/stdc++.h>
using namespace std;
int n,m;
int a[205][205],vis[205];
void bfs(int x){
	queue<int> Q;
	Q.push(x);
	printf("%d ",x);
	vis[x]=1;
	while(!Q.empty()){
		int now=Q.front();
		Q.pop();
		for(int i=1;i<=n;i++){
			if(a[now][i]&&!vis[i]){
				Q.push(i);
				printf("%d ",i);
				vis[i]=1;
			}
		}
	}
}
int main() {
	scanf("%d%d",&n,&m);
	int u,v;
	for(int i=1;i<=m;i++){
		scanf("%d%d",&u,&v);
		a[u][v]=a[v][u]=1;
	}
	int k;
	scanf("%d",&k);
	bfs(k);
    return 0;
}

3.欧拉路径和欧拉回路

欧拉路是指存在这样一种图 , 可以从其中一点出发 , 不重复地走完其所有的边 .  如果欧拉路的起点与终点相同  则称之为欧拉回路

欧拉路存在的充要条件 : 图是连通的 ,因为若不连通不可能一次性遍历所有边。

对于无向图有且仅有两个点 ,与其相连的边数为奇数 ,其他点相连边数皆为偶数 ;对于两个奇数点 , 一个为起点 , 一个为终点 . 起点需要出去 ,终点需要进入 ,故其必然与奇数个边相连 .

对于有向图 除去起点和终点 , 所有点的出度与入度相等 。且起点出度比入度大 1。终点入度比出度大 1。 若起点终点出入度也相同 ，则称为欧拉回路。
可参见鸽巢原理

eg.一笔画问题

Code

 #include <bits/stdc++.h>
using namespace std;
int g[1005][1005], ans[1005], num[1005], idx = 0, n, m, st = 1;
;
void dfs(int i) {
    for (int j = 1; j <= n; j++) {
        if (g[i][j]) {
            g[i][j] = g[j][i] = 0;
            dfs(j);
        }
    }
    ans[++idx] = i;
}
int main() {
    memset(g, 0, sizeof(g));
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        g[x][y] = g[y][x] = 1;
        num[x]++;
        num[y]++;
    }
    for (int i = 1; i <= n; i++) {
        if (num[i] % 2)
            st = i;
    }
    dfs(st);
    for (int i = 1; i <= idx; i++) {
        printf("%d ", ans[i]);
    }
    return 0;
}

4.哈密顿路

哈密顿路径也称作哈密顿链，指在一个图中沿边访问每个顶点恰好一次的路径。

Code

 #include<bits/stdc++.h>
using namespace std;
int n,a[105][105],ans=0;
bool mp[105];
void dfs(int k,int t)
{
    if(t==n){
        ans++;
        return;
    }
    for(int i=1;i<=n;i++)
    {
        if(a[k][i]==1 &&mp[i]==true)
        {
            mp[i]=false;
            dfs(i,t+1);
            mp[i]=true;
        }
    }
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++){
        memset(mp,true,sizeof(mp));
        mp[i]=false;
        dfs(i,1);
    }
    printf("%d",ans);
    return 0;
}

四.最短路问题

最短路径问题是图论研究中的一个经典算法问题， 旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。

1.Floyd

佛洛伊德是最简单的最短路径算法，可以计算图中任意两点间的最短路径。时间复杂度为O(N³)，适用于出现负边权的情况。

算法描述：

(a)初始化：点u、v如果有边相连，则F[u][v]=w[u][v]

如果不相连，则

for(int k=1;k<=n;k++) {
		for(int i=1;i<=n;i++) {
			for(int j=1;j<=n;j++) {
				F[i][j]=max(F[i][j],F[i][k]+F[k][j]);
			}
		}
	}

(c)算法结束：F[i][j]得出的就是任意起点i到任意终点j的最短路径。

疑问：为什么枚举中间点的循环k要放在最外层？

Answer

 可以从一定不经过k点与一定经过k点的三维数组比较中推导出来
动态规划以”途径点集大小”为阶段？
决策需要枚举中转点，不妨考虑也以中转点集为阶段
F[k,i,j]表示”可以经过标号≤k的点中转时”从i到j的最短路
F[0,i,j]=W[i,j]，W为前面定义的邻接矩阵
F[k,i,j]=min{F[k-1,i,j] , F[k-1,i,k]+F[k-1,k,j]}，O(N^3)
k这一维空间可以省略，变成F[i,j]
就成为了我们平时常见的Floyd算法
由于k是DP的阶段循环，所以k循环必须要放在最外层

动态规划以”途径点集大小”为阶段？

决策需要枚举中转点，不妨考虑也以中转点集为阶段 F[k,i,j]表示”可以经过标号≤k的点中转时”从i到j的最短路 F[0,i,j]=W[i,j]，W为前面定义的邻接矩阵 F[k,i,j]=min{F[k-1,i,j] , F[k-1,i,k]+F[k-1,k,j]}，O(N³)

k这一维空间可以省略，变成F[i,j] 就成为了我们平时常见的Floyd算法 由于k是DP的阶段循环，所以k循环必须要放在最外层 。

也就是说每进行一次K的循环，计算的都是任意两点之间只经过前K个中转点（可以不选）的最短路。

使用floyd输出最短路径

Floyd算法输出路径也是采用记录前驱点的方式。因为floyd是计算任意两点间最短路径的算法，F[i][j]记录从i到j的最短路径值。故我们定义pre[i][j]为一个二维数组，记录从i到j的最短路径中，j的前驱点是哪一个。递归还原路径。

初始化pre[i][i]为0，输入相连边时，重置相连边尾结点的前驱

若有无向边：pre[a][b]=a;  pre[b][a]=b; 更新若floyd最短路有更新，那么pre[i][j]=pre[k][j];

Q：(这能不能直接赋值k的值？)

Answer

 不能，因为不一定选了第K个点。

递归输出指两点s，e的最短路，先输出起点s，再将终点e放入递归，输出s+1~e的所有点。

Code

 void print(int x) {    
    if(pre[s][x]==0) return;
    print(pre[s][x]);
    printf(“->%d”,x);
}

2.Dijkstra

预备知识：松弛操作

  原来用一根橡皮筋连接a,b两点，现在有一点k，使得a->k->b比a->b的距离更短，则把橡皮筋改为a->k->b，这样橡皮筋更加松弛。这样说或许不好理解，毕竟两点之间线段最短是常识。可以这样想，如果今天我要去罗马，有很多种选择。当然选择最短的路。但如果最短的那条路太堵了，还不如选远一点但不堵的呢,就可以试着转站。这就是带权的最短路问题。

if(dis[b]<dis[k]+w[k][b])
    dis[b]=dis[k]+w[k][b]

结点分成两组：已经确定最短路、尚未确定最短路 不断从第2组中选择路径长度最短的点放入第1组并扩展 本质是贪心，只能应用于正权图 普通的Dijkstra算法O(N^2) 堆优化的Dijkstra算法O(NlogN)~O(MlogN)

算法描述：

设起点为s，dis[v]表示从指定起点s到v的最短路径，pre[v]为v的前驱，用来输出路径

(a)初始化

memset(dis,+∞)，memset(vis,false)；

(v:1~n)dis[v]=w[s][v]；

dis[s]=0；pre[s]=0；

vis[s]=true；

(b)for(i=1;i<=n-1;i++)

①在没有被访问过的点中找一个相邻顶点k，使得dis[k]是最小的；

②k标记为已确定的最短路vis[k]=true;

③用for循环更新与k相连的每个未确定最短路径的顶点v (所有未确定最短路的点都松弛更新)

if(dis[k]+w[k][v]<dis[v]) dis[v]=dis[k]+w[k][v],pre[v]=k;

(c)算法结束dis[v]为s到v的最短路距离；pre[v]为v的前驱结点，用来输出路径。

Code

 #include <bits/stdc++.h>
using namespace std;
int n,m,s,t;
const int N =100001;
int dis[N];//从起始点到i的最短路
int vis[N];//是否确定最短路
struct edge {
    int v,w;
};
struct node {
    int u,dis;//下标,距离
    bool operator<(const node &tmp)
    const {
        return dis>tmp.dis;//让还没有确定最短路的数以距离 从小到大，每一次选最小的作为松弛点
    }
};
priority_queue<node> Q;
vector<edge> G[N];
int Dijkstra(int S,int T) {
    memset(vis,0,sizeof(vis));
    memset(dis,0x3f,sizeof(dis));
    dis[S]=0;
	Q.push((node){S,0});//将起点压入队列
    while(!Q.empty()) {
    	int u=Q.top().u;//取出起点下标
    	Q.pop();
    	if(vis[u]) continue;//如果已经确定最短路径，continue
    	vis[u]=1;
    	int v,w,siz=G[u].size();
    	for(int i=0;i<siz;i++) {//枚举与u相邻的点
    		v=G[u][i].v,w=G[u][i].w;//取出与它相邻点下的标，与它的距离
    		if(dis[v]>dis[u]+w) {//将起点到此相邻点的距离 与将u作为起点到v的松弛点比较（进行松弛操作）
    			dis[v]=dis[u]+w;
    			Q.push((node){v,dis[v]}); //如果进行松弛操作，压入队列
			}
		}
	}
	return dis[T];
}
int main()
{
    int u,v,w;
    scanf("%d %d %d %d",&n,&m,&s,&t);
    for(int i=0;i<m;i++) {
        scanf("%d %d %d",&u,&v,&w);
        G[u].push_back((edge){v,w});
        G[v].push_back((edge){u,w});
    }
    cout<<Dijkstra(s,t);
    return 0;
}

3.Bellman-Ford算法 与SPFA算法

Bellman-Ford算法：对每条边执行更新，迭代N-1次。 具体操作是对图进行最多n-1次松弛操作，每次操作对所有的边进行松弛，为什么是n-1次操作呢？这是因为我们输入的边不一定是按源点由近至远，万一是由远至近最坏情况就得n-1次，我们可以以一个单链A→B→C→D来举例(由老师写黑板吧) 可以应用于负权图

SPFA:对每条边执行更新，迭代N-1次 SPFA = 队列优化的Bellman-Ford算法 本质上还是迭代——每更新一次就考虑入队 稀疏图上O(kN)，稠密图上退化到O(N^2)

SLF优化：Small Label First, 新入队点与队头比较

LLL优化：Large Label Last, 队头与平均值比较 可以应用于有向负权图

算法实现：

在Bellmanford算法中，有许多松弛是无效的。这给了我们很大的改进的空间。SPFA算法正是对Bellmanford算法的改进。它是由西南交通大学段丁凡1994提出的。它采用了队列和松弛技术。先将源点加入队列。然后从队列中取出一个点(此时该点为源点)，对该点的邻接点进行松弛，如果该邻接点松弛成功且不在队列中，则把该点加入队列。如此循环往复，直到队列为空，则求出了最短路径。           判断有无负环：如果某个点进入队列的次数超过N次则存在负环 ( 存在负环则无最短路径,如果有负环则会无限松弛,而一个带n个点的图至多松弛n-1次)

五.最小生成树

  树有这样一个定理：N个点用N-1条边连接成一个连通块，形成的图形只可能是树，叫做生成树！因此，一个有N个点的连通图，边一定是≥N-1条的！特别的 口袋的天空 ，如果想要连出k棵树，就需要连n-k条边。

1.Kruskal算法

  利用并查集维护。初始时每个点单独为一个集合，把边的权值从小到大排序后依次扫描。如果这条边的u，v在一个集合，那么如果把u，v连上就会形成一个回路，因此不管（见下图）。如果不在一个集合，就合并。

很显然，按照我们的思路，权值为3的这条边是不应该被连的。又因为前面排过序，保证了最小值的准确性

具体流程

(a)初始化

①写出找祖先函数int find_father(int x)

②写出合并函数void union_set(int x , int y)

③写出sort的cmp(结构体a.u , a.v , a.w),对存在的边权(a.w)从小到大排序

④主函数里面：for输入边，for把每个点的父节点初始化为自己,sort排序

⑤MST=0

(b)for(i=1;i<=m;i++)

①if两个点的祖先不是同一个,连接两个点,MST+=边权,边+1;

②if(边==n-1)break;

(c)算法结束：MST即为最小生成树的权值之和。

Code

 #include<bits/stdc++.h>
using namespace std;
struct edge {
	int u,v,c;
}G[10005];
int fa[10005];
int Find(int x) {
	if(fa[x]==x) return x;
	return fa[x]=Find(fa[x]);
}
bool cmp(edge x,edge y) {
	return x.c<y.c;
}
int main() {
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=1;i<=n;i++)
    	fa[i]=i;
    for(int i=1;i<=m;i++) {
    	scanf("%d %d %d",&G[i].u,&G[i].v,&G[i].c);
	}
	sort(G+1,G+m+1,cmp);
	int cnt=0,sum=0;
	for(int i=1;i<=m;i++) {
		int x=Find(G[i].u),y=Find(G[i].v);
		if(x==y) continue;
		fa[x]=y;
		sum=max(G[i].c,sum);
		cnt++;
		if(cnt==n) break;
	}
	printf("%d %d",n-1,sum);
    return 0;
}

2.Prim算法

笔者还是更喜欢Kruskal

以任意一个点为基准点 节点分为两组：

1. 在MST上到基准点的路径已经确定的点

2. 尚未在MST中与基准点相连的点

不断从第2组中选择与第1组距离最近的点加入第1组 类似于Dijkstra，本质也是贪心，O(N^2)

具体流程

  也使用“蓝白点”思想，白点代表已进入最小生成树的点，蓝点代表未进入最小生成树的点。以1为起点生成最小生成树，min[v]表示蓝点v与白点相连的最小边权，MST表示最小生成树的权值之和。

  (a)初始化：min[v]=∞(v≠1);  min[1]=0;  MST=0;

  (b)for(i=1;i<=n;i++)

    ①for寻找min[u],最小的蓝点u;

    ②将u标记为白点;

    ③MST+=min[u];

    ④for与白点u相连的所有蓝点v(可暴力枚举，更好的是求vector的size)

     if(w[u][v]<min[v])   min[v]=w[u][v];

  (c)算法结束：MST即为最小生成树的权值之和。

Code

 #include<bits/stdc++.h>
using namespace std;
int n,ans, a[105][105],m[105],p[105];
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
	    for (int j=1;j<=n;j++)
	        scanf("%d",&a[i][j]);
	memset(m,0x3f,sizeof(m));
	memset(p,0,sizeof(p));
	m[1]=0;
	for (int i=1;i<=n;i++)
	{
		int k=0;
		for (int j=1;j<=n;j++)
		    if (p[j]==0&&m[j]<m[k])
		       k=j;
		p[k]=1;
		ans+=m[k];
		for (int j=1;j<=n;j++)
		    if (p[j]!=1&&a[k][j]<m[j])
		       m[j]=a[k][j];
	}
	cout<<ans<<endl;
	return 0;
}

堆优化和邻接表就不写了吧……（心虚……）

Show time

No.1  走廊泼水节

  给定一棵N个节点的树，要求增加若干条边，把这棵树扩充为完全图，并满足图的唯一最小生成树仍然是这棵树。

求增加的边的权值总和最小是多少。

 题目分析

  首先说明，笔者是看懂的 LINK 这篇博客。

  看到题面，我们首先需要知道完全图是什么。度娘如是说道：“完全图是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连”。相当于题目给了你一颗子树，让你填充。倒着想，如果给了你一颗完全图求最小生成树，你会怎么求？先从小到大排序。然后你会发现对于最小生成树的每两个，如果在完全图中还存在另一边（最小生成树中不包含），那么这一边一定比对于这两点在最小生成树的任意边小。倒回来，你填充的任意边必须比这两点连通的边大。

首先我们设S_x表示为x之前所在的连通块 那么S_y表示为y之前所在的连通块.
假如说点A属于S_x这个集合之中 点B属于S_y这个集合之中.  那么点A与点B之间的距离,必须要大于之前的w,否则就会破坏之前的最小生成树，所以说(A,B)之间的距离最小为w+1。假如说我们知道S_x有p个元素,然后S_y有q个元素。那么将Sx与Sy连通块的所有点相连.显然这个两个连通块会增加.p×q−1条边。然后每一条边的最小长度都为w+1。

所以我们会得出
(w+1)×(p∗q−1)为两个连通块成为完全图的最小代价

Code

 #include <bits/stdc++.h>
using namespace std;
int s[6005],fa[6005];
struct Edge {
	int u,v,w;
}edge[6005];
bool cmp (Edge x,Edge y) {
	return x.w<y.w;
}
int Find(int x) {
	if(fa[x]==x) return x;
	return fa[x]=Find(fa[x]);
}
int main() {
	int t;
	scanf("%d",&t);
	while(t--) {
		int n;
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
			fa[i]=i,s[i]=1;
		for(int i=1;i<n;i++) {
			scanf("%d %d %d",&edge[i].u,&edge[i].v,&edge[i].w);
		}
		sort(edge+1,edge+n,cmp);
		int ans=0;
		for(int i=1;i<n;i++) {
			int x=Find(edge[i].u),y=Find(edge[i].v);
			if(x==y) continue;
			fa[x]=y;
			ans+= (edge[i].w+1) * (s[x]*s[y]-1);
			s[y]+=s[x];
		}
		printf("%d\n",ans);
	}
	return 0;
}

No.2 最短路上的统计

既然是多源最短路，就应该用Floyd来做。

我们先用三重循环跑一遍Floyd，先求得最短路。

对于每一个ask，依次枚举每一个点看最短路经不经过。

Code

 #include<bits/stdc++.h>
using namespace std;
int n,m,a[101][101],ans[101][101],p,x,y;
int main()
{
    memset(a,127/3,sizeof(a));
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i){
        scanf("%d%d",&x,&y);
        a[x][y]=1;a[y][x]=1;  //权值为1
    }
    for(int i=1;i<=n;++i)     //初始化一下
      a[i][i]=0;
    for(int k=1;k<=n;k++)     //Floyed
        for(int i=1;i<=n;++i)
          for(int j=1;j<=n;++j)
            a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
    scanf("%d",&p);
	for(int i=1;i<=p;++i){
		scanf("%d%d",&x,&y);
		if(ans[x][y]==0){
			for(int k=1;k<=n;++k)   //枚举点k
			  if(a[x][k]+a[k][y]==a[x][y]) ans[x][y]++; //如果点k在最短路上，ans++
			ans[y][x]=ans[x][y];
		}
		printf("%d\n",ans[x][y]);  //输出
	}
}

No.3 Kuglarz

我们可以发现，我们要确定 i 里面有没有东西，有两种方法：

1.直接看 ( i , i )
2.看 ( i , j ) 和 ( i + 1 , j ) 
我们可以把点变成边权， i 变成 i − 1 到 i的一条边。（ 对于（i,i）这种自环情况可以设置一个虚点0 ）
那我们就发现我们要让最小的边权使得所有的点都被连起来。

如果我们知道每一个位置是否有小球，那么就可以知道区间[ 0 , i ] (1≤i≤n)的奇偶性。

相反，如果我们知道区间 [ 0 , i ] (1≤i≤n)的奇偶性，那么我们就可以知道每个位置是否有小球。所以我们只用花费最小代价求知每个[0,i]区间的奇偶性。

如果我们知道区间[0,i-1]和[i,j]的奇偶性，就可以知道[0,j]的奇偶性。同理，如果知道[0,j]和[i,j]的奇偶性，我们就可以知道[0,i-1]的奇偶性。

位置0是我们虚构的节点，该位置上一定没有小球，所以[0,0]为偶。

对于一次询问[i,j]，我们将[0,i-1]和[0,j]之间连一条权值为c_i,j的边，表示知道其中一个，花费c_i,j​代价可以知道另一个。

只要保证所有点和[0,0]联通，即整个图联通，即可保证知道所有[0,i]的奇偶性，就可以知道所有位置上是否有小球。

图已经建好了，直接求最小生成树即可。边数较多，建议使用Prim，但笔者很菜只会kruscal。

Code

 #include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct Edge {
	ll u,v,w;
}edge[5000005];
ll fa[5000005];
bool cmp(Edge x,Edge y) {
	return x.w<y.w;
}
ll Find(ll x) {
	if(x==fa[x]) return x;
	return fa[x]=Find(fa[x]);
}
int main() {
	//freopen("kuglurz.in","r",stdin);
	//freopen("kuglurz.out","w",stdout);
	ll n,a,idx=0;
	scanf("%lld",&n);
	for(ll i=1;i<=n;i++)
		fa[i]=i;
	for(ll i=1;i<=n;i++) {
		for(ll j=i;j<=n;j++) {
			scanf("%lld",&a);
			edge[++idx].u=i-1,edge[idx].v=j,edge[idx].w=a;
		}
	}
	sort(edge+1,edge+idx+1,cmp);
	ll sum=0,cnt=0;
	for(ll i=1;i<=idx;i++) {
		ll x=Find(edge[i].u),y=Find(edge[i].v);
		if(x==y) continue;
		cnt++;
		fa[x]=y;
		sum+=edge[i].w;
		if(cnt==n) break;
	}
	printf("%lld",sum);
	return 0;
}

No.4 棋盘上的守卫

  在( i,j )这个点上我们可以放置两种守卫，第一种是横向守卫，第二种是竖向守卫，所以它们之间只能选择一种，可以抽象成一条边，链接的是横向的第 i 个阶段，竖向的第 j 个阶段，为了方便，我们将 j的下标写作j + n。

可以得到一条性质： 对于任意一个点 i， 若 i > n，则这是列的阶段。

• 将行列看成 n+m个点。将每个格点放置守卫看成所在行列连了一条边，然后把每条边定向，如果被指向表示当前格点对当前 行/列 进行了保护。

• 这样就会有 n+m个点，n+m条有向边，同时每条边最多有 1 的入度。形成了基环树森林。

如果当前两个点在同一集合，那么判断是否已经成环，如果不成环还可以加上这一条边。
如果当前两个点不在同一个集合，那么判断是否存在一个点所在集合没有成环，如果是，可以加边。

Code

 //基环树
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct Edge {
    ll u, v, w;
} edge[100005];
ll fa[100005];
bool vis[100005];
ll Find(ll x) {
    if (x == fa[x])
        return x;
    return fa[x] = Find(fa[x]);
}
bool cmp(Edge x, Edge y) { return x.w < y.w; }
int main() {
    ll n, m, a, idx = 0;
    scanf("%lld %lld", &n, &m);
    for (ll i = 1; i <= n; i++) {
        for (ll j = 1; j <= m; j++) {
            scanf("%lld", &a);
            edge[++idx].u = i, edge[idx].v = j + n, edge[idx].w = a;
        }
    }
    for (ll i = 1; i <= m + n; i++) {
        fa[i] = i;
    }
    sort(edge + 1, edge + idx + 1, cmp);
    ll ans = 0;
    for (ll i = 1; i <= idx; i++) {
        ll x = Find(edge[i].u), y = Find(edge[i].v);
        if (vis[x] && vis[y]) { //如果已经成环
            continue;
        } else if (x == y) { //如果在一个集合,连一条边可以成环
            vis[y]=vis[x] = 1;//记录这两边已经成一个环
            ans += edge[i].w;
        } else {
            fa[x] = y;
            ans += edge[i].w;
            vis[y] = vis[y] | vis[x];//如果原x或y与别的树成环 ，记录y是已成环树
        }
    }
    printf("%lld", ans);
    return 0;
}