Machine Learning 学习笔记 03 最小二乘法、极大似然法、交叉熵

损失函数

神经网络里的标准和人脑标准相比较 相差多少的定量表达。

最小二乘法

首先要搞明白两个概率模型是怎么比较的。有三种思路，最小二乘法、极大似然估计，交叉熵

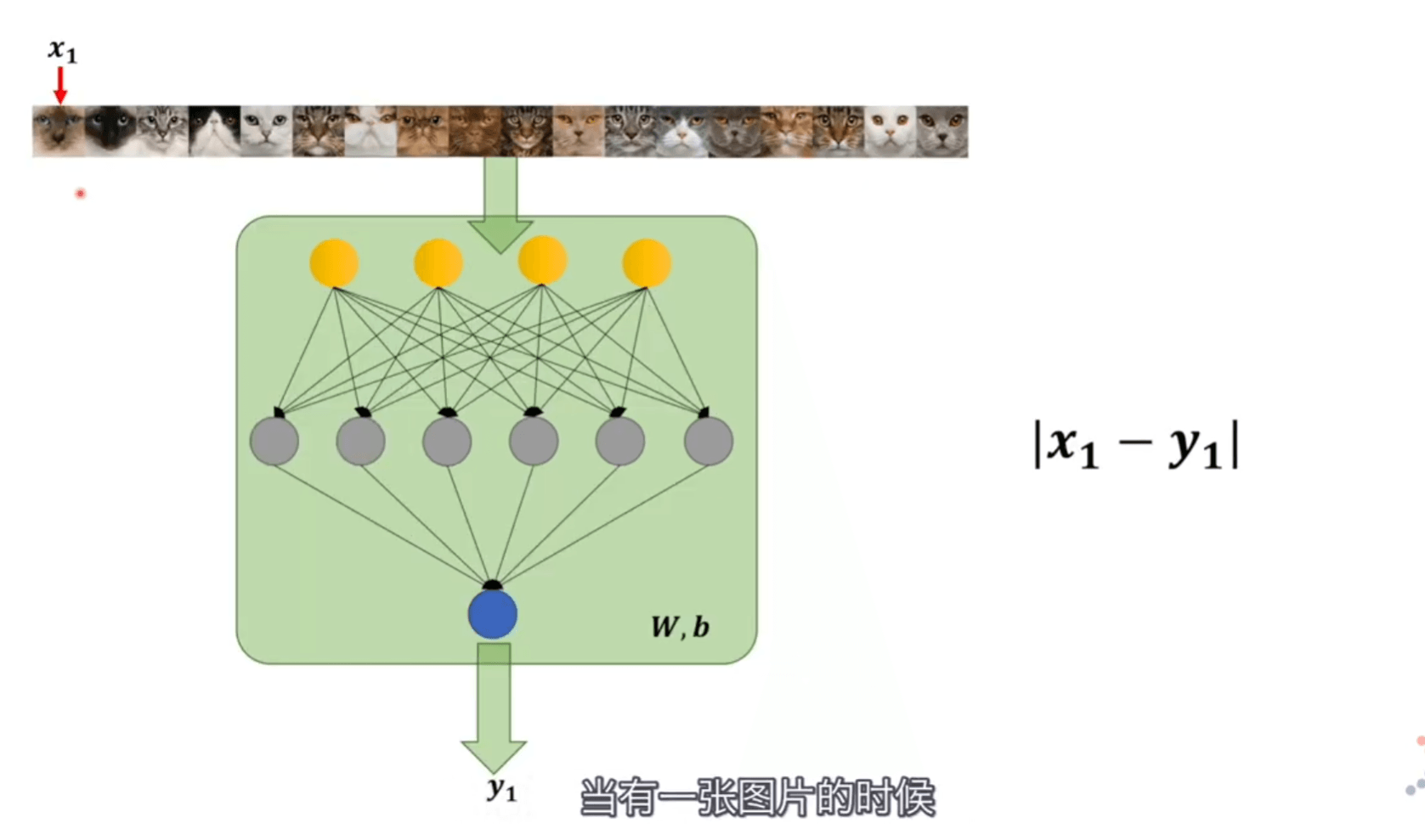
当一张图片人脑判断的结果是 \(x1\)，神经网络判断的结果是 \(y1\)，直接把它们相减 \(\left|x_{1}-y_{1}\right|\) 就是他们相差的范围。我们将多张图片都拿过来判断加起来，当最终值最小的时候，\(\min \sum_{i=1}^{n}\left|x_{i}-y_{i}\right|\) 就可以认定两个模型近似。

但是绝对值在定义域内不是全程可导的，所以可以求平方 \(\min \sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}\)

就这是最小二乘法，但是只用它判断两个概率模型差别有多少，去作为损失函数会比较困难。所以引入极大似然估计

极大似然估计

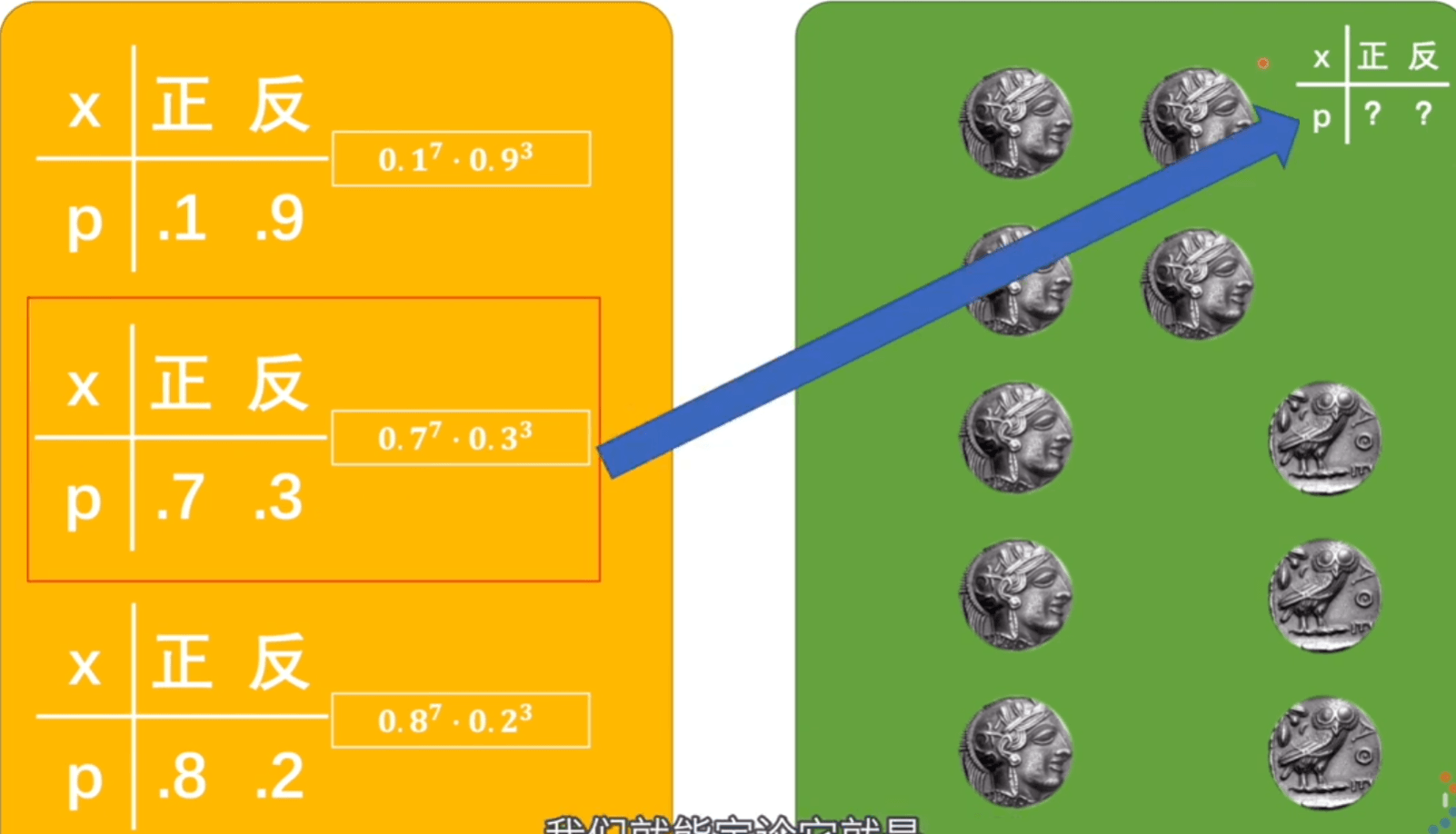
似然值是真实的情况已经发生，我们假设它有很多模型，在这个概率模型下，发生这种情况的可能性就叫似然值。

挑出似然值最大的，那可能性也就越高，此时的概率模型应该是与标准模型最接近的。

\[\begin{array}{l} P\left(C_{1}, C_{2}, C_{3}, \ldots, C_{10} \mid \theta\right) \\ P\left(x_{1}, x_{2}, x_{3}, x_{4}, \ldots, x_{n} \mid W, b\right) \end{array} \]

\(\theta\) 是抛硬币的概率模型，\(W,b\) 是神经网络的概率模型。前者结果是硬币是正还是反，后者结果是图片到底是不是猫。

\[\begin{array}{l} P\left(x_{1}, x_{2}, x_{3}, x_{4}, \ldots, x_{n} \mid W, b\right) \\ =\prod_{i=1}^{n} P\left(x_{i} \mid W, b\right) \end{array} \]

在神经网络是这样的参数下，输入的照片如果是猫概率是多少、如果不是猫概率是多少，所有图片判断后，相乘得到的值就是似然值。取到极大似然值就是最接近的值。

但在训练的时候 \(W、b\) 无论输入什么样的照片都是固定的值，如果我们都用猫的照片来确定的话标签都是\(1\)，那就没有办法进行训练，理论可行却没有操作性。但是我们还可以利用条件，训练神经网络的时候既可以得到 \(x_{i}\) 也可以得到 \(y_{i}\)， \(y_{i}\) 的输出结果依赖 \(W,b\) 。每次输入照片不一样，\(y_{i}\) 的结果也就不一样。

\[\begin{array}{l} =\prod_{i=1}^{n} P\left(x_{i} \mid W, b\right) \\ =\prod_{i=1}^{n} P\left(x_{i} \mid y_{i}\right) \end{array} \]

\(x_{i}\) 的取值是 \(0、1\) ，符合二项伯努利分布，概率分布表达式为

\[f(x)=p^{x}(1-p)^{1-x}=\left\{\begin{array}{ll} p, & x=1 \\ 1-p, & x=0 \end{array}\right. \]

\(x=1\) 就是图片为猫的概率。而 \(p\) 就是 \(y_{i}\) (神经网络认定是猫的概率)，将其带入替换 $ P\left(x_{i} \mid y_{i}\right)$

\[=\prod_{i=1}^{n} y_{i}^{x_{i}}\left(1-y_{i}\right)^{1-x_{i}} \]

我们更喜欢连加，在前面加 \(log\) ，并化简

\[\begin{array}{l} \log \left(\prod_{i=1}^{n} y_{i}^{x_{i}}\left(1-y_{i}\right)^{1-x_{i}}\right) \\ =\sum_{i=1}^{n} \log \left(y_{i}^{x_{i}}\left(1-y_{i}\right)^{1-x_{i}}\right) \\ =\sum_{i=1}^{n}\left(x_{i} \cdot \log y_{i}+\left(1-x_{i}\right) \cdot \log \left(1-y_{i}\right)\right) \end{array} \]

所以，求极大似然值，就是求如下公式

\[\begin{array}{l} \max \left(\sum_{i=1}^{n}\left(x_{i} \cdot \log y_{i}+\left(1-x_{i}\right) \cdot \log \left(1-y_{i}\right)\right)\right) \\ \min -\left(\sum_{i=1}^{n}\left(x_{i} \cdot \log y_{i}+\left(1-x_{i}\right) \cdot \log \left(1-y_{i}\right)\right)\right) \end{array} \]

复习一下对数

1. $\log _{a}(1)=0 $
2. $ \log _{a}(a)=1 $
3. \(负数与零无对数\)
4. \(\log _{a} b * \log _{b} a=1\)
5. $ \log _{a}(M N)=\log _{a} M+\log _{a} N $
6. $\log _{a}(M / N)=\log _{a} M-\log _{a} N $
7. $ \log _{a} M^{n}=n \log _{a} M(\mathrm{M}, \mathrm{N} \in \mathrm{R}) $
8. $ \log _{a^{n}} M=\frac{1}{n} \log _{a} M $
9. $a^{\log _{a} b}=b $

交叉熵

要想直接比较两个模型，前提是两个模型类型是同一种，否则就不能公度。概率模型如果想要被统一衡量，我们需要引入熵（一个系统里的混乱程度）。

信息量

我们想获取信息量的函数，就要进行定义。并找寻能让体系自洽的公式。

\[{f}({x}):=\text { 信息量 }\\ {f}( 阿根廷夺冠 )={f}( 阿根廷进决赛 )+{f}( 阿根廷赢了决赛 ) \\ f\left(\frac{1}{8}\right)=f\left(\frac{1}{4}\right)+f\left(\frac{1}{2}\right)\\ P(\text { 阿根廷夺冠 })=P(\text { 阿根廷进决赛 }) \cdot {P} \text { (阿根廷赢了决赛 })\\ \]

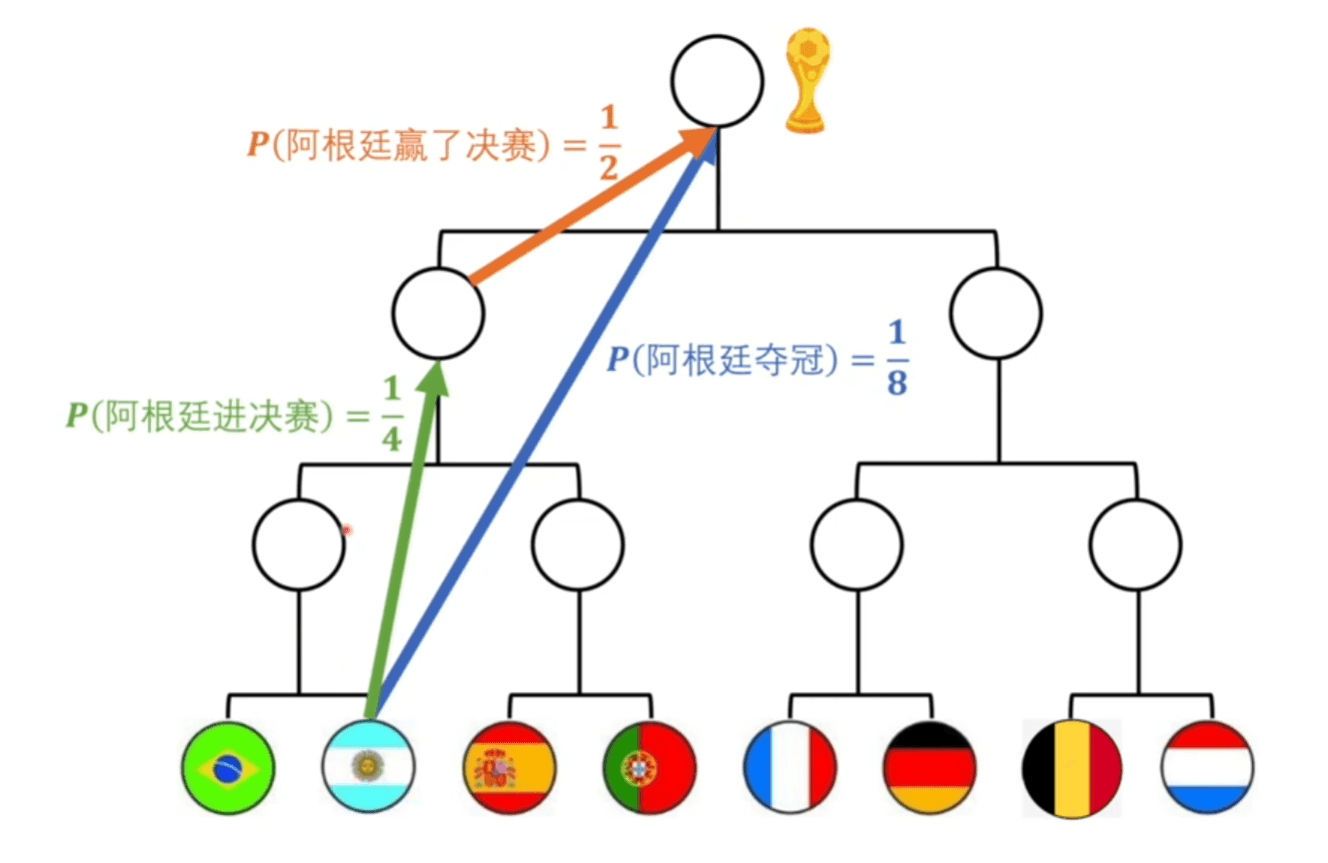
将上面的第四条公式带入第三条得到如下第二条。为了使信息量定义能让体系自洽，我们给定定义 \(log\)，这样符合相乘变相加的形式。

\[\begin{array}{c} f(x):=? \log _{?} x \\ f\left(x_{1} \cdot x_{2}\right)=f\left(x_{1}\right)+f\left(x_{2}\right) \end{array} \]

为了符合我们最直观的感觉，因为概率越小，信息量越大。而 \(log\) 函数单调递增，我们转换方向。

\[\begin{array}{c} f(x):=-\log _{2} x \\ f\left(x_{1} \cdot x_{2}\right)=f\left(x_{1}\right)+f\left(x_{2}\right) \end{array} \]

看计算机里多少位数据，给计算机输入一个16位数据，输入之前随便取的值是 \(1/2^{16}\) 的概率 ，输入之后的概率直接变为了 \(1\) 。信息量就是 \(16\) 比特。

信息量可以理解为一个事件从原来不确定到确定它的难度有多大，信息量大，难度高。

熵不是衡量某个具体事件，而是整个系统的事件，一个系统的从不确定到确定难度有多大

它们都是衡量难度，单位也可以一样都是比特。

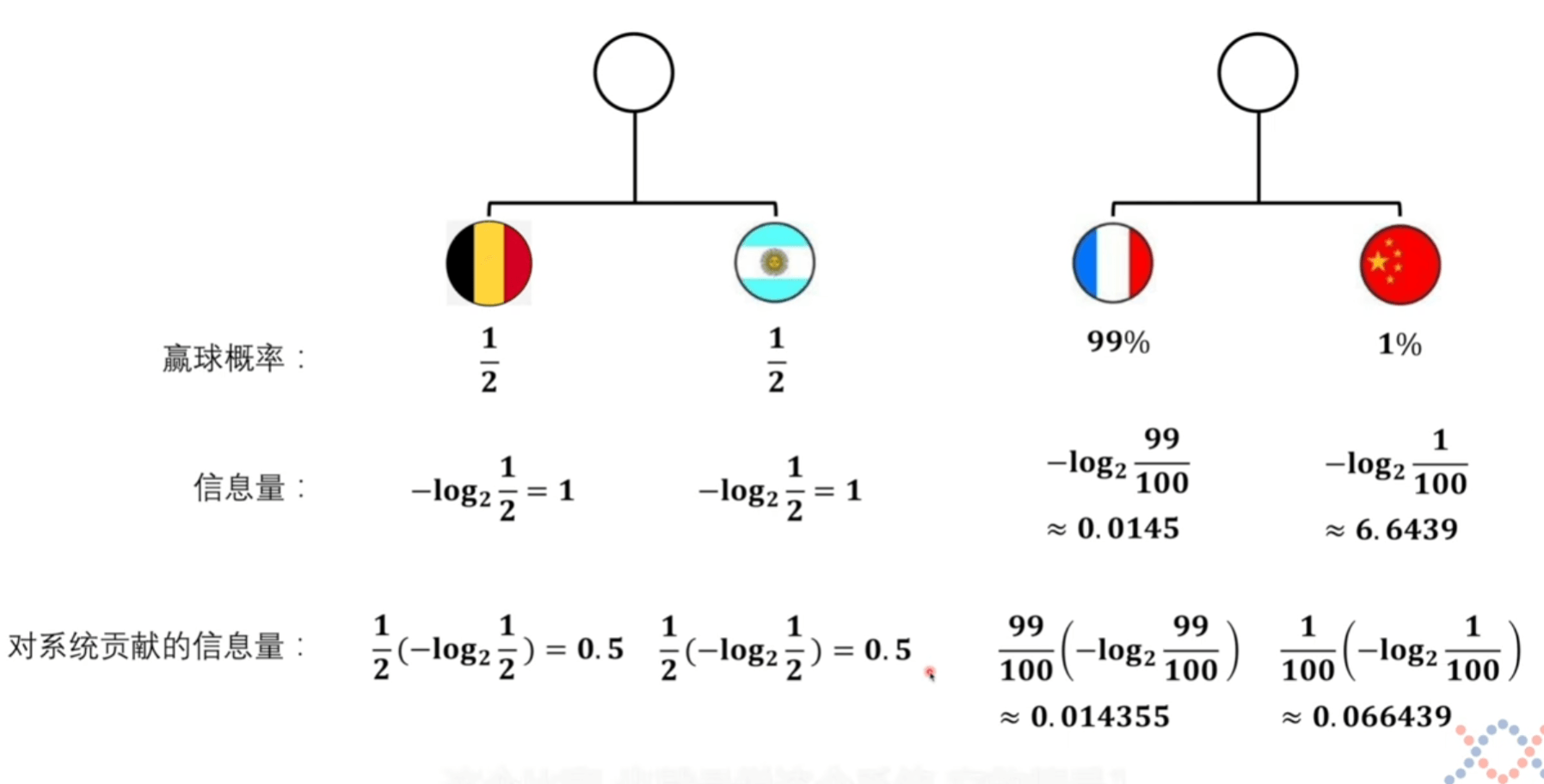
系统熵的定义

将上方对系统贡献的信息量可以看成是期望的计算。

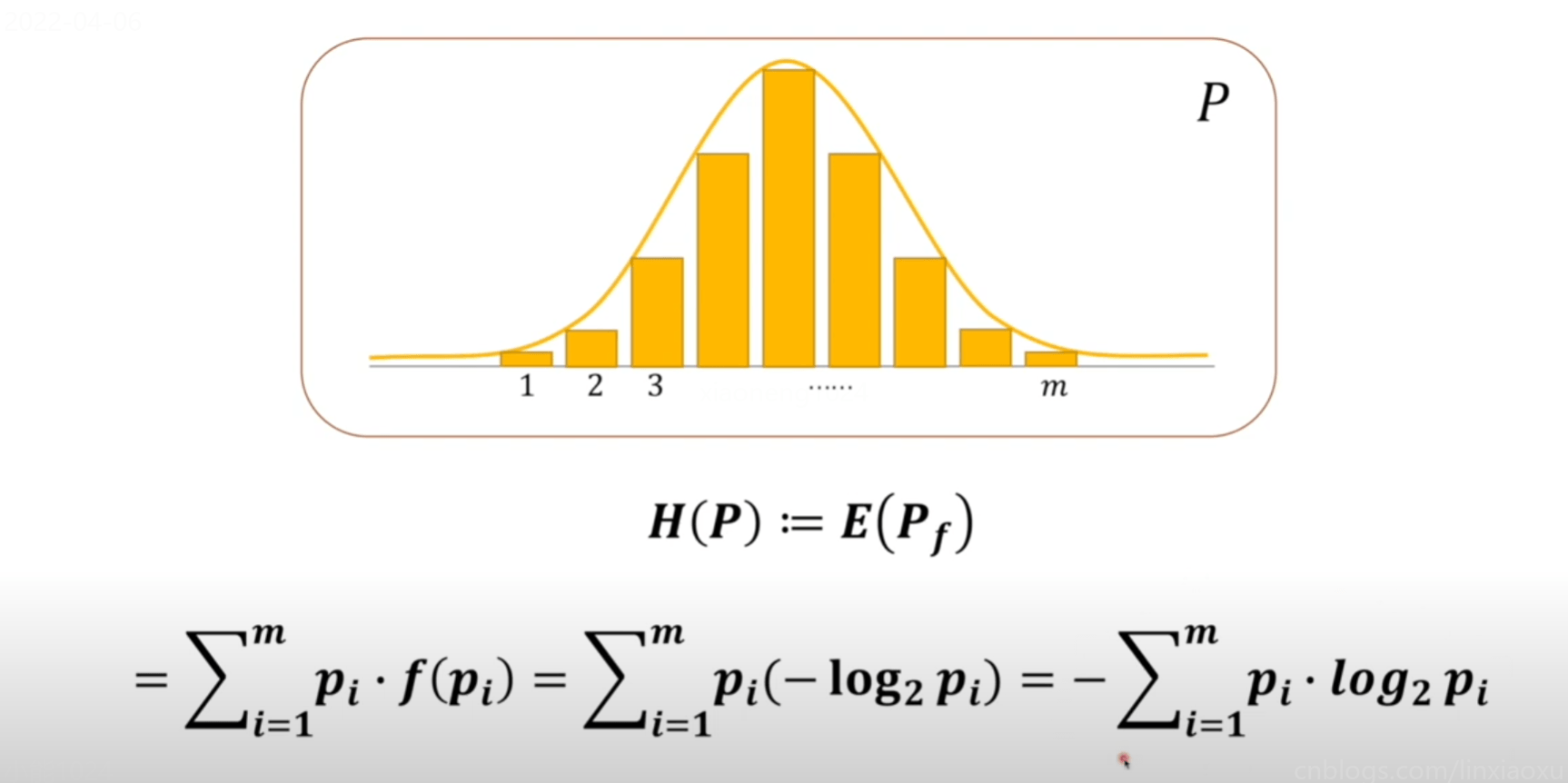
KL散度

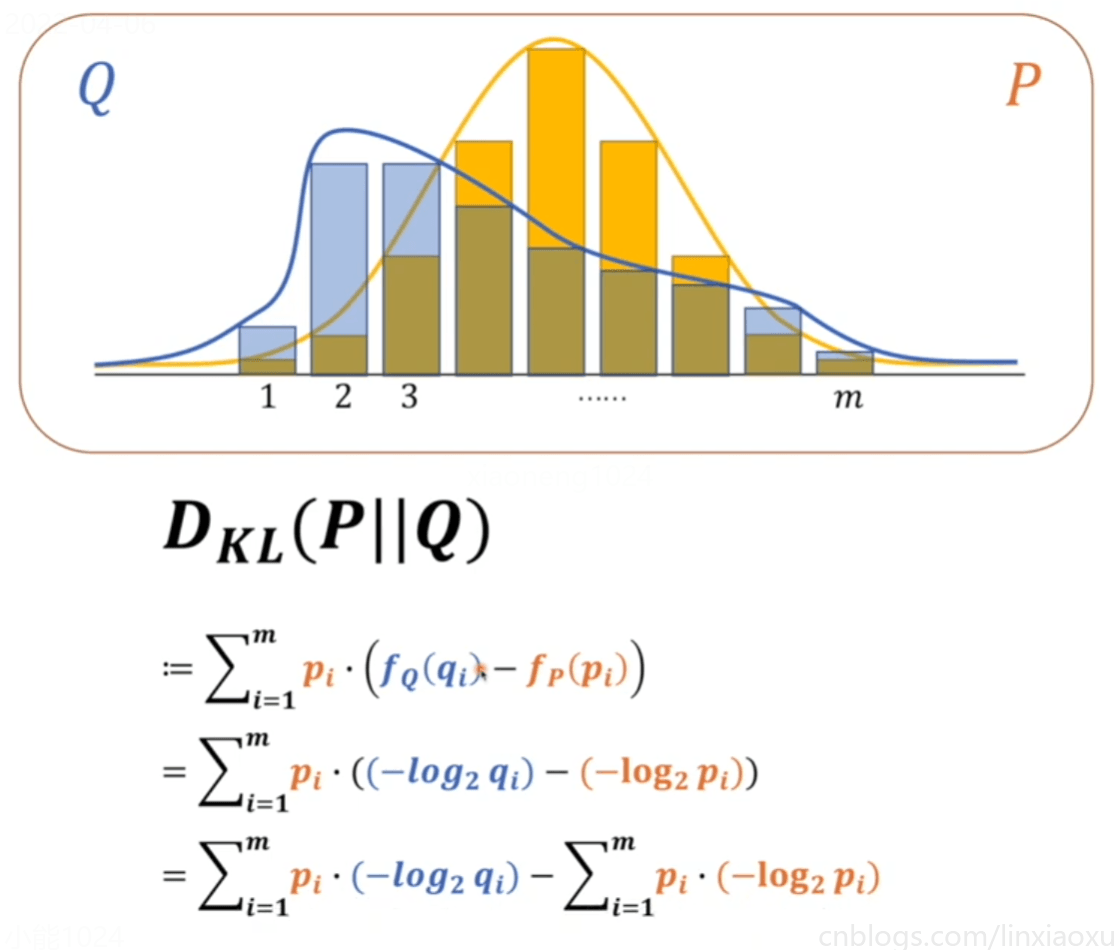
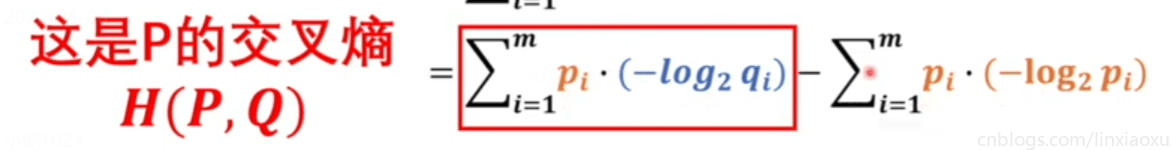
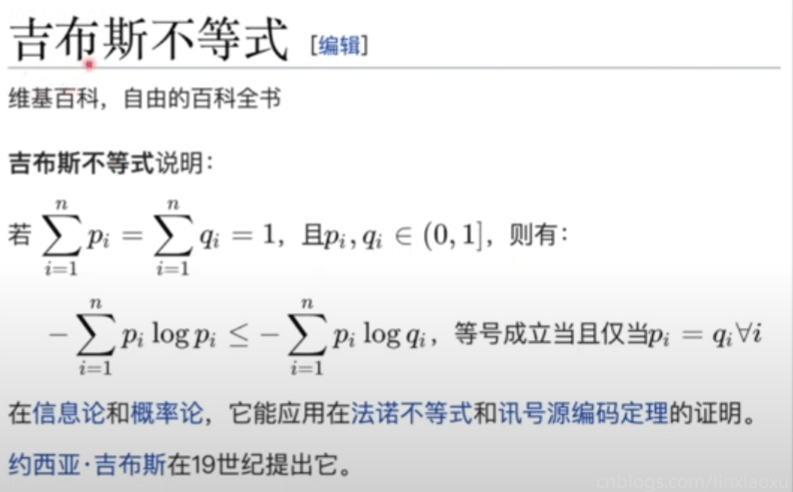
KL散度绝对是大于等于\(0\)的，当\(Q、P\)相等的时候等于\(0\)，不相等的时候一定大于\(0\)

为了让\(Q、P\)两个模型接近，所以必须使交叉熵最小

交叉熵中 \(m\) 是两个概率模型里事件更多的那个，换成 \(n\) 是图片数量。

对\(m\)选择的解释：假如\(p\)的事件数量是\(m\)，\(q\)的事件数量是\(n\)，\(m＞n\)，那么写成\(∑\)求和，用较大的\(m\)做上标。就可以分解为，\(∑1到n+∑n+1到m\)，那么对于\(q\)来说，因为\(q\)的数量只有\(n\)，那么对应的\(q\)的部分\(∑n+1到m\)都等于\(0\)。

\[\begin{array}{l} \boldsymbol{H}(\boldsymbol{P}, \boldsymbol{Q}) \\ =\sum_{i=1}^{m} p_{i} \cdot\left(-\log _{2} q_{i}\right) \\ =\sum_{i=1}^{n} x_{i} \cdot\left(-\log _{2} q_{i}\right) \\ =-\sum_{i=1}^{n}\left(x_{i} \cdot \log _{2} y_{i}+\left(1-x_{i}\right) \cdot \log _{2}\left(1-y_{i}\right)\right) \end{array} \]

\(P\) 是基准，要被比较的概率模型，我们要比较的人脑模型，要么完全是猫要么不是猫。

\(x_{i}\) 有两种情况，而 \(y_{i}\) 只判断图片有多像猫，并没有去判断相反的这个猫有多不像猫，而公式里的 \(x_{i}\) 与 \(q_{i}\) 要对应起来，当 \(x_{i}\) 为 \(1\) ，要判断多像猫，当 \(x_{i}\) 为 \(0\) 的时候，要判断不像猫的概率。

最后我们推导出来，公式跟极大似然推导出来的是一样的。但是从物理角度去看两者是有很大不同的，只是形式上的一样。

• 极大似然法里的 \(log\) 使我们按习惯引入的，把连乘换成相加。而交叉熵的 \(log\) 是写在信息量定义里的，以 \(2\) 为底，计算出来的单位是比特，是有量纲的。
• 极大似然法求的是最大值，我们按习惯求最小值。而交叉熵负号是写在定义里的。