Python 分形算法__代码里开出来的艺术之花

1. 前言

分形几何是几何数学中的一个分支，也称大自然几何学，由著名数学家本华曼德勃罗（法语：BenoitB.Mandelbrot）在 1975 年构思和发展出来的一种新的几何学。

分形几何是对大自然中微观与宏观和谐统一之美的发现，分形几何最大的特点：

整体与局部的相似性： 一个完整的图形是由诸多相似的微图形组成，而整体图形又是微图形的放大。

局部是整体的缩影，整体是局部的放大。
具有自我叠加性： 整体图形是由微图形不断重复叠加构成，且具有无限叠加能力。

什么是分形算法？

所谓分形算法就是使用计算机程序模拟出大自然界的分形几何图案，是分形几何数学与计算机科学相融合的艺术。

由于分形图形相似性的特点，分形算法多采用递归实现。

2. 分形算法

2.1 科赫雪花

科赫雪花是由瑞典数学家科赫在 1904 年提出的一种不规则几何图形，也称为雪花曲线。

分形图形的特点是整体几何图形是由一个微图形结构自我复制、反复叠加形成，且最终形成的整体图案和微图形结构一样。在编写分形算法时，需要先理解微图案的生成过程。

科赫雪花的微图案生成过程：

先画一条直线。科赫雪花本质就由一条直线演化而成。
三等分画好的直线。
取中间线段，然后用夹角为 60° 的两条等长线段替代。
可在每一条线段上都采用如上方式进行迭代操作，便会构造出多层次的科赫雪花。

科赫微图形算法实现：

使用 Python 自带小海龟模块绘制，科赫雪花递归算法的出口的是画直线。

import turtle

'''

size：直线的长度

level: 科赫雪花的层次

'''

def koch(size, level):

    if n == 1:

        turtle.fd(size)

    else:

        for i in [0, 60, -120, 60]:

            turtle.left(i)

            # 旋转后，再绘制

            koch(size // 3, level - 1)

参数说明：

size： 要绘制的直线长度。
level： 科赫雪花的层次。

0 阶和 1 阶科赫雪花递归流程：

import turtle

turtle.speed(100)

def ke_line(line_, n):

    if n == 0:

        turtle.fd(line_)

    else:

        line_len = line_ // 3

        for i in [0, 60, -120, 60]:

            turtle.left(i)

            ke_line(line_len, n - 1)

# 原始直线长度

line = 300

# 移动小海龟到画布左下角

turtle.penup()

turtle.goto(-150, -150)

turtle.pendown()

# 1 阶科赫雪花

di_gui_deep = 1

ke_line(line, di_gui_deep)

turtle.done()

2 阶科赫雪花：

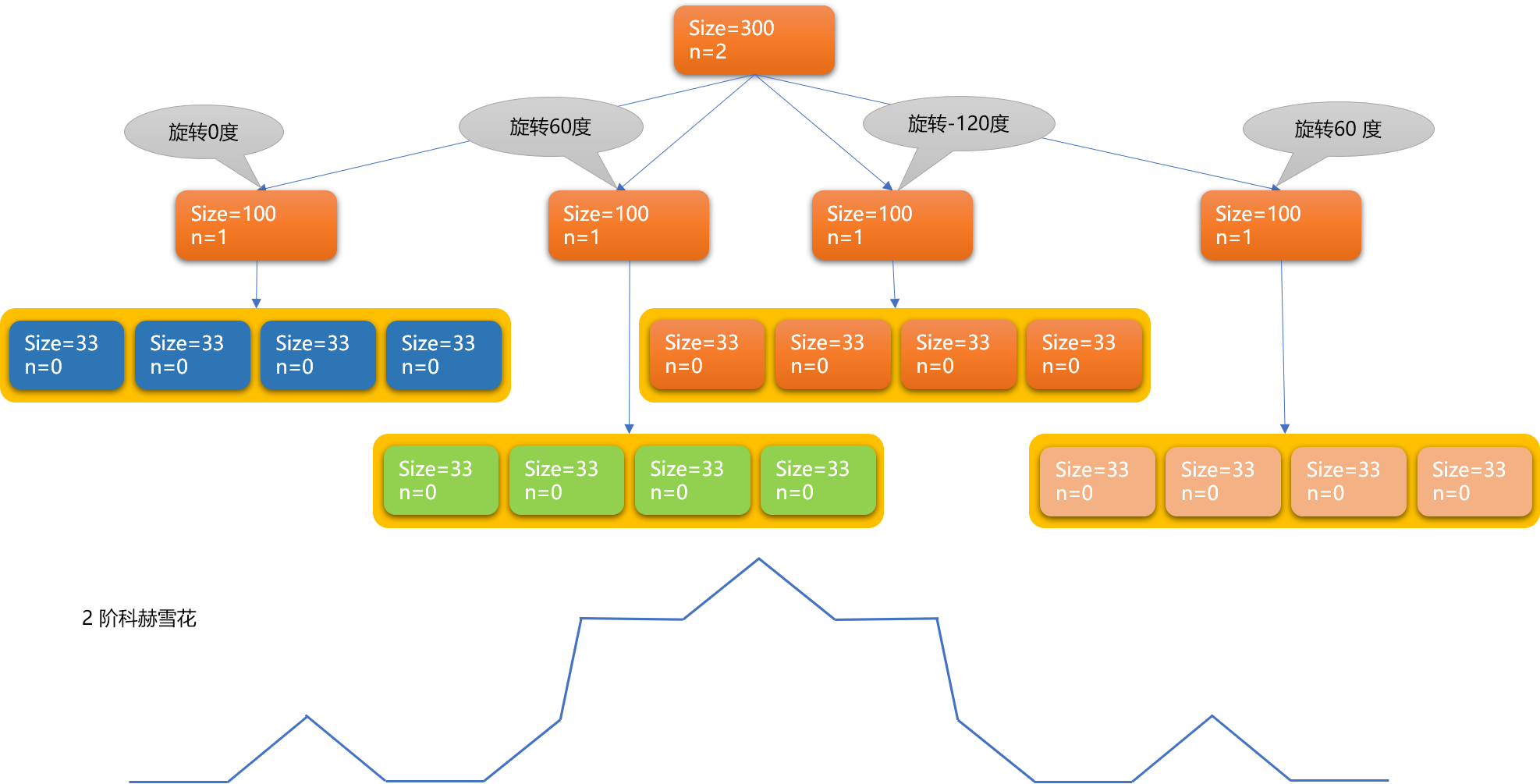
可以多画几个科赫雪花，布满整个圆周。

import turtle

turtle.speed(100)

def ke_line(line_, n):

    if n == 0:

        turtle.fd(line_)

    else:

        line_len = line_ // 3

        for i in [0, 60, -120, 60]:

            turtle.left(i)

            ke_line(line_len, n - 1)

# 原始线长度

line = 300

# 移动小海龟画布左下角

turtle.penup()

turtle.goto(-150, -150)

turtle.pendown()

# 几阶科赫雪花

di_gui_deep = int(input("请输入科赫雪花的阶数："))

while True:

    # 当多少科赫雪花围绕成一个圆周时，就构成一个完整的雪花造型

    count = int(input("需要几个科赫雪花："))

    if 360 % count != 0:

        print("请输入 360 的倍数")

    else:

        break

for i in range(count):

    ke_line(line, di_gui_deep)

    turtle.left(360 // count)

turtle.done()

4 个 3 阶科赫雪花： 每画完一个后旋转 90 度，然后再绘制另一个。

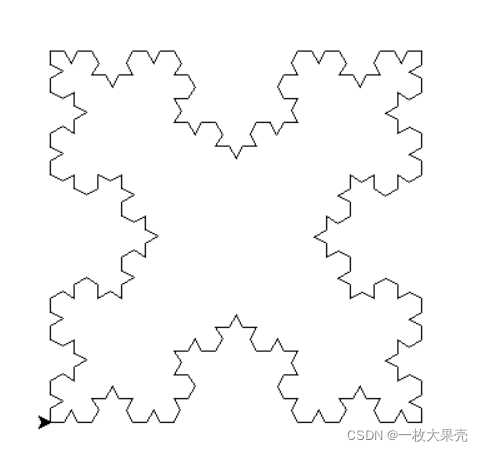
6 个 3 阶科赫雪花： 每画完一个后，旋转 60 度再画另一个。

科赫雪花的绘制并不难，本质就是画直线、旋转、再画直线……

2.2 康托三分集

由德国数学家格奥尔格·康托尔在1883年引入，是位于一条线段上的一些点的集合。最常见的构造是康托尔三分点集，由去掉一条线段的中间三分之一得出。

构造过程：

绘制一条给定长度的直线段，将它三等分，去掉中间一段，留下两段。
再将剩下的两段再分别三等分，同样各去掉中间一段，剩下更短的四段……
将这样的操作一直继续下去，直至无穷，由于在不断分割舍弃过程中，所形成的线段数目越来越多，长度越来越小，在极限的情况下，得到一个离散的点集，称为康托尔点集。

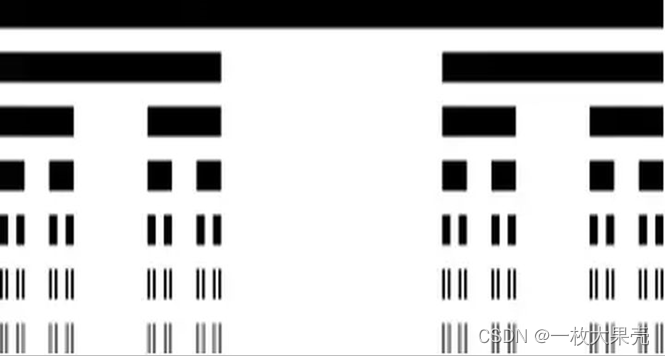
编码实现： 使用递归实现。

import turtle

''''

(sx,sy)线段的开始位置

(ex,ey)线段的结束位置

'''

turtle.speed(100)

turtle.pensize(2)

def draw_kt(sx, sy, ex, ey):

    turtle.penup()

    # 小海龟移动开始位置

    turtle.goto(sx, sy)

    turtle.pendown()

    # # 小海龟移动结束位置

    turtle.goto(ex, ey)

    # 起始点与结束点之间的距离

    length = ex - sx

    # 如果直线长线大于 5 则继续画下去

    if length > 5:

        # 左边线段的开始 x 坐标

        left_sx = sx

        # y 坐标向下移动 30

        left_sy = sy - 50

        # 左边线段的结束坐标

        left_ex = sx + length / 3

        left_ey = left_sy

        # 右边线段的开始坐标

        right_sx = ex - length / 3

        right_sy = ey - 50

        # 右边线段的结束坐标

        right_ex = ex

        right_ey = right_sy

        draw_kt(left_sx, left_sy, left_ex, left_ey)

        draw_kt(right_sx, right_sy, right_ex, right_ey)

draw_kt(-300, 200, 300, 200)

turtle.done()

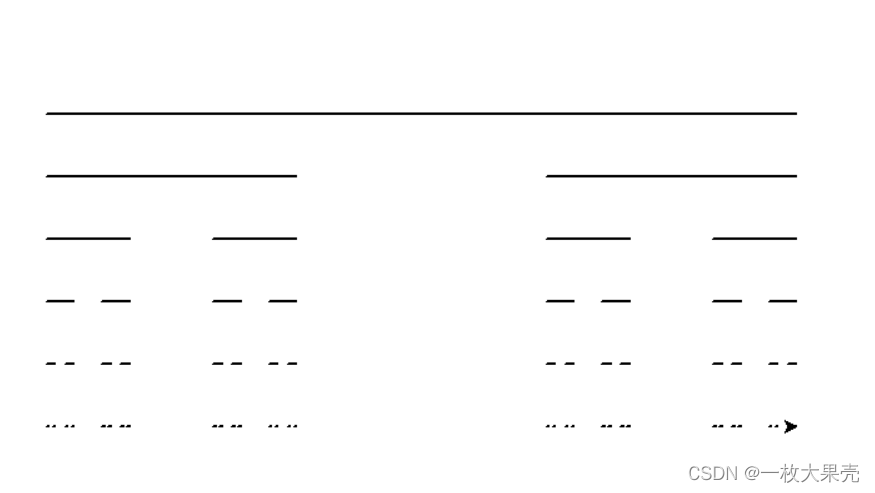
康托三分集的递归算法很直观。

2.3 谢尔宾斯基三角形

谢尔宾斯基三角形（英语：Sierpinski triangle）由波兰数学家谢尔宾斯基在1915年提出。

构造过程：

取一个实心的三角形（最好是等边三角形）。
沿三边中点的连线，将它分成四个小三角形。
去掉中间的那一个小三角形。
对其余三个小三角形重复上述过程直到条件不成立。

编码实现： 谢尔宾斯基三角形就是不停的画三角形，在编码之前约定三角形点之间的关系以及绘制方向如下图所示。

import turtle

import math

turtle.speed(100)

'''

 通过连接 3 个点的方式绘制三角形

 pos是元组的元组((x1,y1),(x2,y2),(x3,y3))

'''

def draw_triangle(pos):

    turtle.penup()

    # 移到第一个点

    turtle.goto(pos[0])

    turtle.pendown()

    # 连接 3 个点

    for i in [1, 2, 0]:

        turtle.goto(pos[i])

# 计算三角形任意两边的中点坐标

def get_mid(p1, p2):

    return (p1[0] + p2[0]) / 2, (p1[1] + p2[1]) / 2

'''

绘制 谢尔宾斯基三角形

'''

def sierpinski_triangle(*pos):

    # 用给定的点绘制三角形

    draw_triangle(pos)

    p1, p2, p3 = pos

    # 计算三角形的边长

    side = math.fabs((p3[0] - p1[0]) / 2)

    # 如果边长满足条件，继续绘制其它三角形

    if side > 10:

        # p1和p2线段 的中心点

        p1_p2_center_x, p1_p2_center_y = get_mid(p1, p2)

        # p2和p3线段 的中心点

        p2_p3_center_x, p2_p3_center_y = get_mid(p2, p3)

        # p1和p3线段 的中心点

        p1_p3_center_x, p1_p3_center_y = get_mid(p1, p3)

        # 绘制左下角三角形

        sierpinski_triangle(p1, (p1_p2_center_x, p1_p2_center_y), (p1_p3_center_x, p1_p3_center_y))

        # 绘制上边三角形

        sierpinski_triangle((p1_p2_center_x, p1_p2_center_y), p2, (p2_p3_center_x, p2_p3_center_y))

        # 绘制右下角三角形

        sierpinski_triangle((p1_p3_center_x, p1_p3_center_y), (p2_p3_center_x, p2_p3_center_y), p3)

# 第一个点指左边点，第二点指上面的点，第三个指右边的点。

sierpinski_triangle((-200, -100), (0, 200), (200, -100))

turtle.done()

代码执行之后的结果：

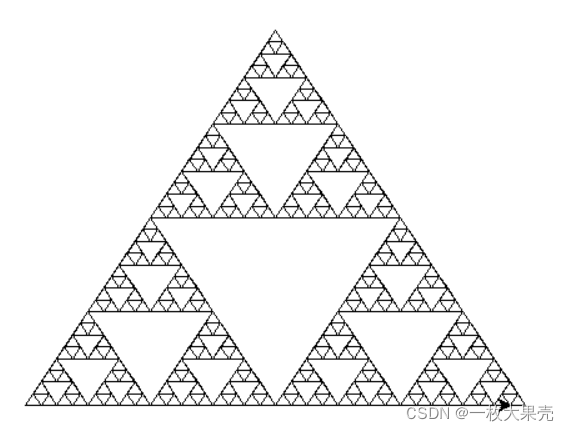
用随机的方法（Chaos Game），绘制谢尔宾斯基三角形：

构造过程：

任意取平面上三点 A,B,C，组成一个三角形。

在三角形 ABC 内任意取一点 P，并画出该点。

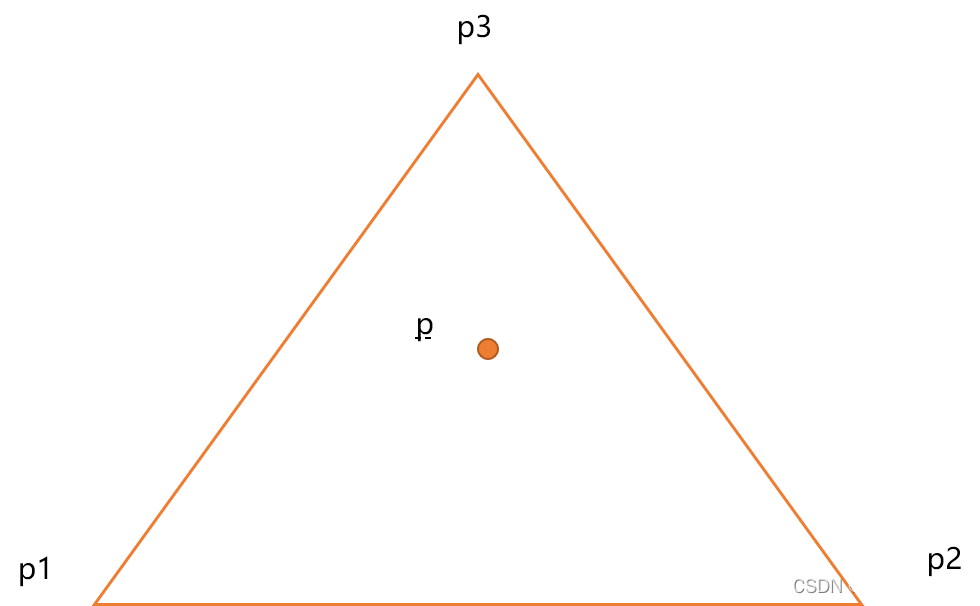
找出 P 和三角形其中一个顶点的中点，并画出来。

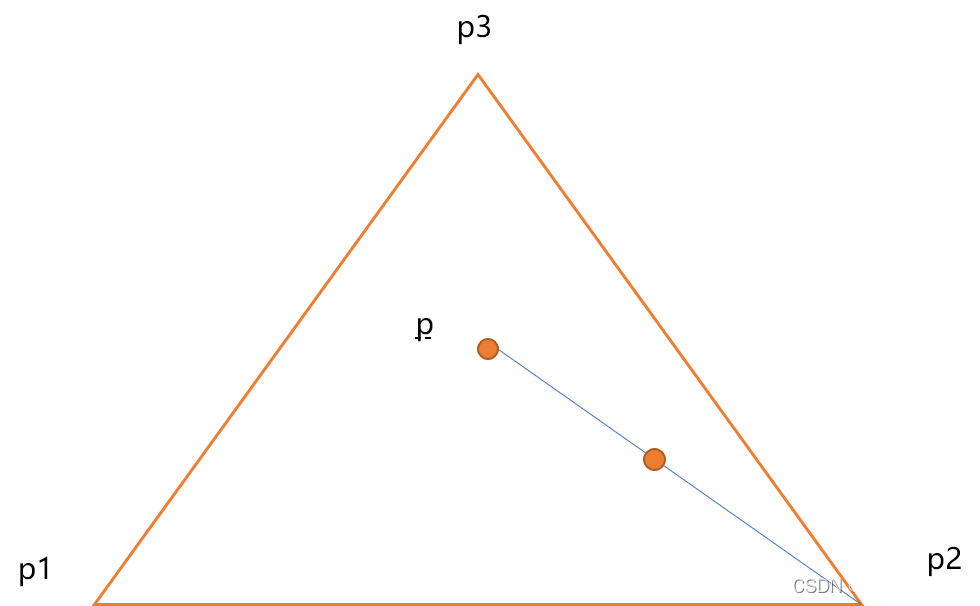
把刚才找出来的中心点和三角形的任一顶点相连接，同样取其中点，并画出来。

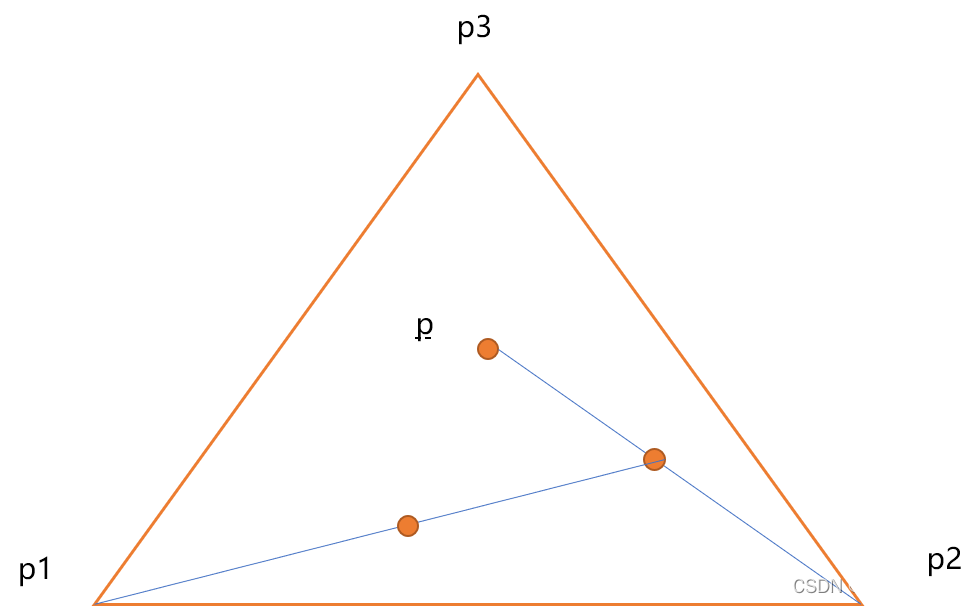
重复上述流程，不停的获取中心点。

注意，是画点，上面的线段是为了直观理解中心点位置。

编码实现：

import turtle

import random

turtle.speed(100)

turtle.bgcolor('black')

colors = ['red', 'green', 'blue', 'orange', 'yellow']

# 画等边三角形

def draw_triangle(pos):

    turtle.penup()

    turtle.goto(pos[0])

    turtle.pendown()

    for i in [1, 2, 0]:

        turtle.goto(pos[i])

def sierpinski_triangle(*pos):

    # 画三角形

    draw_triangle(pos)

    p1, p2, p3 = pos

    # 在三角形中任取一点

    ran_x, ran_y = (p1[0] + p3[0]) / 2, (p2[1] + p3[1]) / 2

    for i in range(10000):

        # 画点

        turtle.penup()

        turtle.goto(ran_x, ran_y)

        turtle.pendown()

        turtle.dot(3, colors[i % 5])

        # 随机选择 3 个顶点的一个顶点

        ran_i = random.randint(0, 2)

        ding_p = pos[ran_i]

        # 计算任意点和顶点的中心点

        ran_x, ran_y = (ran_x + ding_p[0]) / 2, (ran_y + ding_p[1]) / 2

sierpinski_triangle((-200, -100), (0, 200), (200, -100))

turtle.done()

随机法是一个神奇的存在，当点数量很少时，看不出到底在画什么。当点的数量增加后，如成千上万后，会看到谢尔宾斯基三角形跃然于画布上，不得不佩服数学家们天才般的大脑。

下图是点数量为 10000 时的谢尔宾斯基三角形，是不是很震撼。

2.4 分形树

绘制分形树对于递归调用过程的理解有很大的帮助，其实前面所聊到的递归算法都是树形递进。分形树能很形象的描述树形递归的过程。

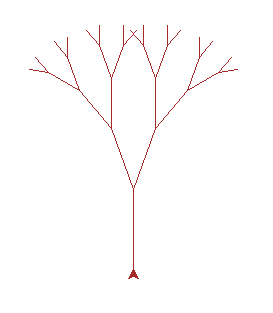
分形树的算法实现：

import turtle

def draw_tree(size):

    if size >= 20:

        turtle.forward(size) # 1

        # 画右边树

        turtle.right(20)

        draw_tree(size - 40) # 2

        # 画左边树

        turtle.left(40)

        draw_tree(size - 40)

        # 后退

        turtle.right(20)

        turtle.backward(size)

turtle.left(90)

draw_tree(80)

turtle.done()

为了理解分形树的递归过程，如上代码可以先仅画一个树干两个树丫。

下面以图示方式显示左右两边的树丫绘制过程。

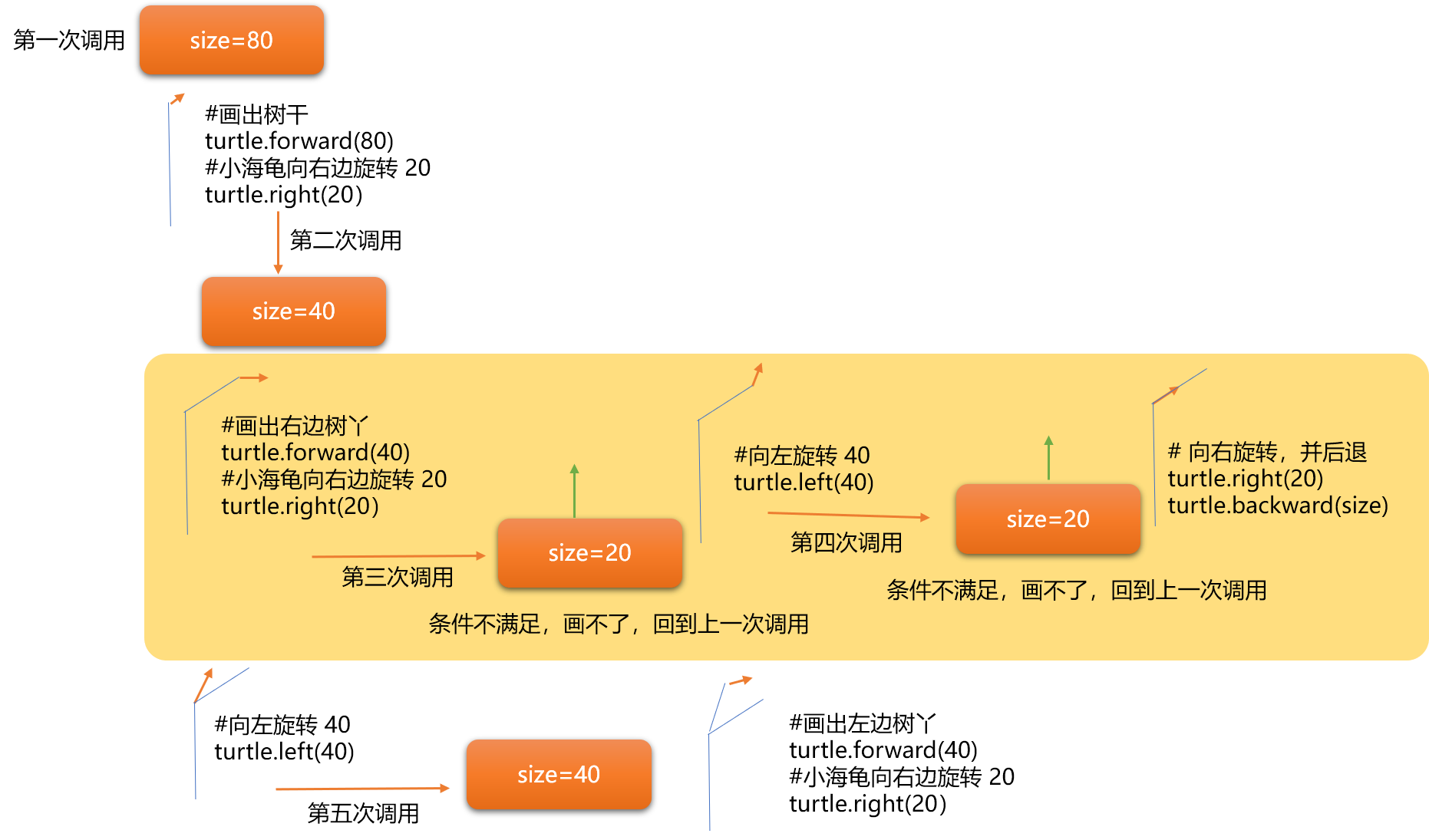
3. 总结

分形几何是大自然对数学的馈赠，当然这离不开数学家们的发现与研究，通过计算机科学对分形几何的模拟，可以以可视化的方式更直观地研究分形几何学。这也是计算机科学对于各学科的巨大贡献。