[题解] Codeforces Dytechlab Cup 2022 1737 A B C D E 题解

傻*Dytechlab还我rating！(不过目前rating还没加上去，据说E是偷的说不定要unrated)

实在没预料到会打成这样。。。

求点赞

A. Ela Sorting Books

从前往后一位一位确定答案。用一个数组记录当前每个字母库存的数量，要确定答案的某一位时，枚举前$min(\frac nk,26)$个字母，找到第一个库存为0的字母，则当前这位的答案就是这个字母。然后把字典序在这个字母之前的字母库存都-1就行。最后把库存中剩下的字母随便塞进未塞满的块就行了。

B. Ela's Fitness and the Luxury Number

询问[l,r]中的Luxury数的个数，一看就知道用[1,r]中的减去[1,l-1]中的。假设一个Luxury数被表示成了$a \cdot b$的形式，其中$a \leq b$。题目要求$a=\lfloor \sqrt{a\cdot b}\rfloor$，转化一下得到$a \cdot b < (a+1)^2$，进一步得到$a \leq b < a+2+\frac 1a$，也就是$a \leq b \leq a+2$。这对于所有的$a \geq 1$都满足。容易发现每个Luxury数都只能被一组合法的$a,b$表示，每组合法的$a,b$都能表示一个Luxury数。假设现在要询问[1,x]中的Luxury数个数，分别求出该区间中能表示成$a^2,a(a+1),a(a+2)$的数的个数就行了。这里建议用二分，直接调用sqrt函数的话可能会有精度问题。

时间复杂度$O(t\cdot log(l+r))$。

C. Ela and Crickets

一眼丁真，鉴定为纯纯的傻*题。完全无法区分OI老手和菜鸡。

对于初始的L型，我们把他凹进去的那个位置，以及所有与这个位置横坐标、纵坐标的奇偶性都相同的位置称为"不可到达的"。手动操作几步，发现这些位置确实永远无法到达。

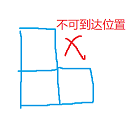
其他位置则是可到达的，大概长成这样：

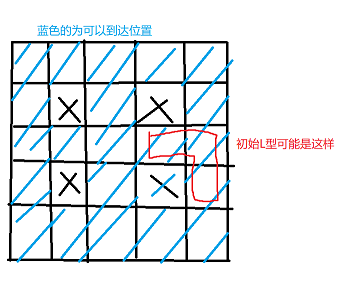
手玩一下发现对于任意的初始L型位置，所有的可到达位置都可以被走到。

有一个例外：当L型的中间一个位置在棋盘左上角时，只能走到第一行和第一列的位置。其他四个角同理：

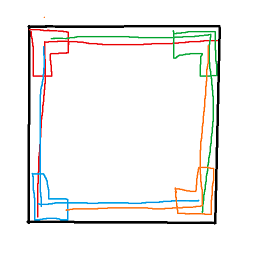
一个技巧：已知L型三个点的坐标，求凹进去那个点的坐标，直接把已知的三个点横纵坐标分别去异或就行了。

我一开始判L型在角上判错了，后来又发现有一个地方在一个询问内同时输出了YES和NO，直接导致这场打的和*一样。自闭.jpg

D. Ela and the Wiring Wizard

一开始的"魔法"操作其实是，把一条边的一个端点沿着与其相连的一条边进行滑动。如果我们滑动了一条边，那不能白滑，最后肯定是要走它的；把它作为"轨道"给其他的边滑也是不优的。观察发现我们最后走的路径一定只由一条边组成，如果多于一条，我们可以把最小的那条拿出来不断滑动，覆盖路径上所有的其他边，这样一定不劣。枚举最后走的那条边(就算不在1~n的某条简单路径上也可以)，想办法把它的两个端点分别滑到1和n。有两种滑法：

两个点分别通过最短路滑到1和n。当前被枚举的这条边只会被两条最短路覆盖最多一次，先滑最短路覆盖了这条边的那个端点即可。
题目里说了滑动过程中是允许自环的，所以我们可以先把两个端点的其中一个滑动到某个位置x，再把另一个用1次操作通过被枚举的边本身滑到x(形成自环)，然后两个端点分道扬镳，各自通过最短路滑到1或n。

注意这里的最短路指的是边权为1的最短路，可以用floyd求出。

时间复杂度$O(n^3)$。

E. Ela Goes Hiking

就差1分钟调完，改了两个字符就过了

比赛公告评论里说是从noip.ac偷的(也可能只是撞了)

考虑求出每只蚂蚁赢的方案数，最后除以总方案数得到概率。n=1的特判。

对于某一种方向选择的状态，先把蚂蚁分段：

一开始，最左和最右(如果存在)两段中的蚂蚁都会合成一个大小$\geq 1$的蚂蚁；中间的每一段，从左往右数第一个向左走的蚂蚁会吃掉这一段中所有向右走的蚂蚁，并且继续向左。

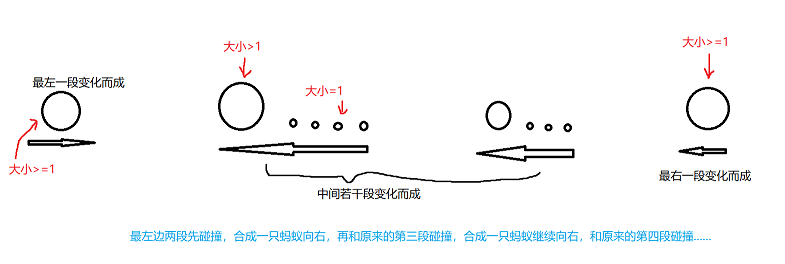
如果最初处在最右边一段的蚂蚁想赢，那它一定是整个序列中最靠右的蚂蚁，并且最靠右一段的长度不小于n的一半。用等比数列求和求出方案数。

如果中间某一段的蚂蚁想赢，那他一定是这一段中从左往右数第一个向左的蚂蚁。这一段中向右的蚂蚁个数要足够多，保证他不被左边所有蚂蚁构成的一只大蚂蚁吃掉。也是等比数列求和计算。现在这只蚂蚁已经和它左边的所有蚂蚁合体，要去吃这一段中剩下向左走的蚂蚁，以及右边其他段中的蚂蚁。为了计算它右边蚂蚁的方案数，我们可以计算出一个数组$win_i$，表示合理选择最后i只蚂蚁的方向，使得如果前n-i只蚂蚁合体向右推，能够吃穿全场的方案数。转移这里不讲了，只要时刻保证当前蚂蚁团大小不$\geq$前面蚂蚁个数之和即可。可以用前缀和优化转移做到$O(n)$(需要一个额外的dp数组，因为每一个中间段都分前后两段，所以一共是两个dp数组和两个前缀和数组)。

如果最左边一段的蚂蚁想赢，那最左边一段的蚂蚁数量一定>1,且赢的一定是序列中第2只蚂蚁。用上面的win数组计算答案即可。

时间复杂度$O(n)$。