P1886 滑动窗口 /【模板】单调队列 方法记录

原题链接

滑动窗口 /【模板】单调队列

题目描述

有一个长为 \(n\) 的序列 \(a\)，以及一个大小为 \(k\) 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is \([1,3,-1,-3,5,3,6,7]\), and \(k = 3\)。

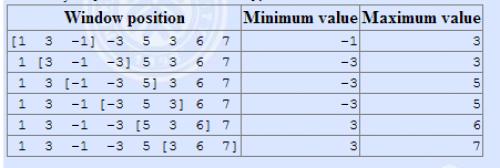
输入格式

输入一共有两行，第一行有两个正整数 \(n,k\)。

第二行 \(n\) 个整数，表示序列 \(a\)

输出格式

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

样例 #1

样例输入 #1

8 3
1 3 -1 -3 5 3 6 7

样例输出 #1

-1 -3 -3 -3 3 3
3 3 5 5 6 7

提示

【数据范围】

对于 \(50\%\) 的数据，\(1 \le n \le 10^5\)；

对于 \(100\%\) 的数据，\(1\le k \le n \le 10^6\)，\(a_i \in [-2^{31},2^{31})\)。

算法：单调队列

单调队列的性质

性质1：单调性

队列中的元素必须满足单调性。如果要求区间最大值，则队列单调递减；否则队列单调递增。即：队首就是要求的元素。

性质2：有序性

事实上，元素在原序列中的相对位置和在队列中的相对位置不变

我们可能进行的操作（“队列”指我们用到的单调序列，“原序列”指输入的序列）

一．当队列中无元素时，直接将原序列中的元素从队尾入队；

二．当队列中有元素时，面对即将进入的元素，若队列中的元素小于即将进入的元素，则队列中的元素不可能成为窗口中的最小值，队列中的元素从队尾出队，新元素从队尾入队。这样以来，队列中的元素就保证是单调递增的；

三．当有新元素进入时，由于不知道之后进入的元素是否比它小，那么这个元素依然有可能成为窗口中的最小值；

四．模拟窗口滑动：如果当前遍历位置与队首位置的区间大于窗口，则重复执行队首右移；

五．生成答案：当遍历的位置第一次超过窗口大小时，每遍历一个元素就会生成一个答案。由于维护的队列单调递增，则每次队首元素就是答案。

程序上的操作参见代码注释。

点击查看代码

#include<iostream>
#include<cstdio>
using namespace std;
const int N=1000005;
int n,k,h,t;
int a[N],q1[N],q2[N];
int main()
{
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	//t--队尾出，h++队首出，t++队尾进
	//q1[],q2[]储存的都是位置,只有a[]储存的是值
	for(int i=1;i<=n;i++)
	{
		while(h<=t&&i-q1[h]>=k) h++;
		while(h<=t&&a[i]<a[q1[t]]) t--;
		q1[++t]=i;
		if(i>=k) printf("%d ",a[q1[h]]);
	}
	puts("");
	for(int i=1;i<=n;i++)
	{
		while(h<=t&&i-q2[h]>=k) h++;
		while(h<=t&&a[i]>a[q2[t]]) t--;
		q2[++t]=i;
		if(i>=k) printf("%d ",a[q2[h]]);
	}
	return 0;
}

参考：

https://blog.csdn.net/qaqwqaqwq/article/details/120429563

https://www.luogu.com.cn/blog/hankeke/solution-p1886