kmp、z算法、exkmp

一、kmp算法

1、基本概念

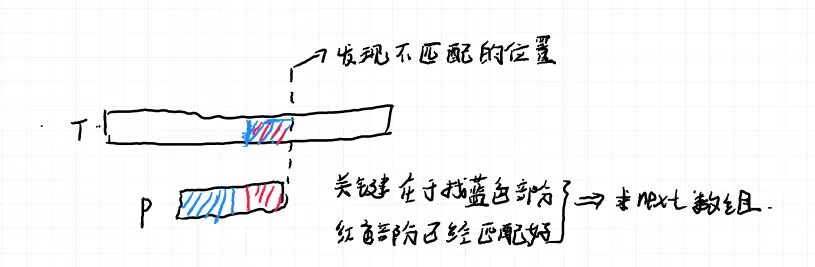
• 模式串：P
• 匹配串：T
• kmp算法精髓：找打一个最大的x，使得T[s+1，...,s+k]的后x个字符，和P的前x个字符相同。

2、next数组

next数组：记录模式串最长公共前后缀

3、相关代码

//求next数组伪代码
next[1] = 0
k = 0
for i = 2 to len(P):
    while(k > 0) and (p[k + 1] != p[i]):
	    k = next[k]
	if(p[k + 1] == p[i]):
	    k++
	next[i]= k

//模式串与匹配串匹配伪代码
j = 0 //模式串P的下标
for i = 1 to len(T)://匹配串T的下标
    while(j > 0) and (T[i] != p[j + 1]):
	    j = next[j]
	if T[i] == P[j + 1]:
	    j ++
	if j == len(P):
	    printf("match")
		j = next[j]

二、Z算法

1、z函数

• 对于一个字符串S和一个下标i(i > 1),令Z[i]表示S和S[i,...,|S|]的最长公共前缀

    0 1 2 3 4 5 6 7 8 9
S = a a b c c a a b x a
Z[5] = 3
Z[6] = 1
Z[7] = 0

2、z box

3、z算法

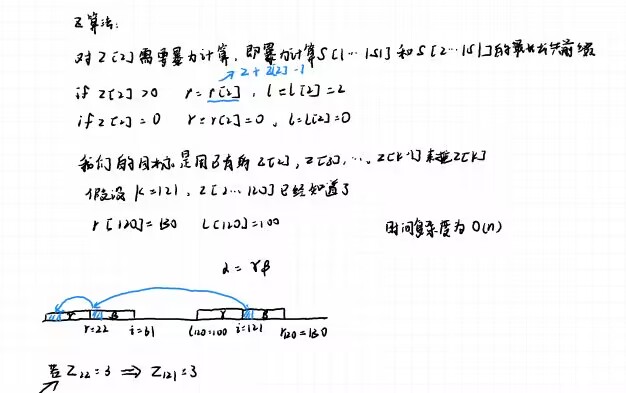
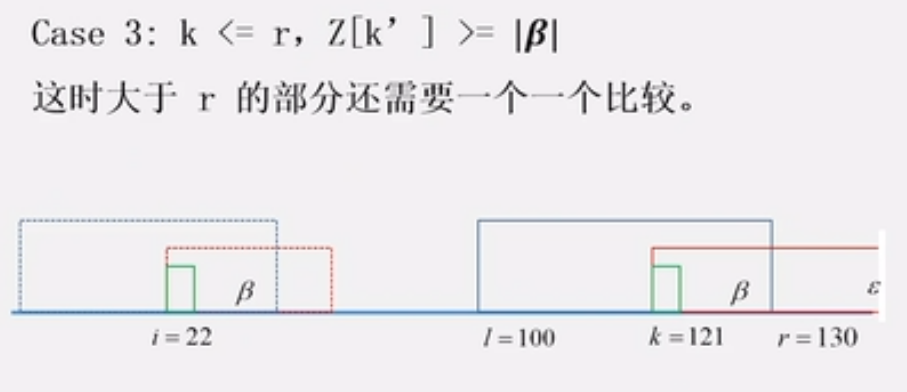
代码部分

//初始化Z[],暴力计算Z[2]
for(int i = 1; i <= n; i++) z[i] = 0;
int l, r;
while(st[1 + z[2]] == st[2 + z[2]]) z[2] ++;
l = 2, r = l + z[2];
//枚举i,分三种情况依次计算Z[i]
for(int i = 3; i <= n; i++){
    if(i > r){
	    while(st[l + z[i]] == st[i + z[i]]) z[i] ++;
		l = i, r = i + z[i] - 1;
	}
	else{
	    if(z[i - l + 1] < r - i + 1) z[i] = z[i - l + 1];
		else{
		    z[i] = r - i;
			while(st[l + z[i]] == st[i + z[i]]) z[i] ++;
			l = i, r = i + z[i] - 1;
		}
	}
}