C# 算术表达式求值（后缀法），看这一篇就够了

一、种类介绍

算术表达式有三种：前缀表达式、中缀表达式和后缀表达式。一般用的是中缀，比如1+1，前后缀就是把操作符移到前面和后面，下面简单介绍一下这三种表达式。

1、前缀表示法

前缀表示法又叫波兰表示法，他的操作符置于操作数的前面（例：+ 1 2），是波兰数学家扬·武卡谢维奇1920年代引入的，用于简化命题逻辑。因为我们一般认为操作符是在操作数中间的，所以在日常生活中用的不多，但在计算机科学领域占有一席之地。一般的表示法对计算机来说处理很麻烦，每个符号都要考虑优先级，还有括号这种会打乱优先级的存在，将使计算机花费大量的资源进行解析。而前缀表示法没有优先级的概念，他是按顺序处理的。举个例子：9-2*3这个式子，计算机需要先分析优先级，先乘后减，找到2*3，再进行减操作；化成前缀表示法就是：- 9 * 2 3，计算机可以依次读取，操作符作用于后一个操作数，遇到减就是让9减去后面的数，而跟着9的是乘，也就是说让9减去乘的结果，这对计算机来说很简单，按顺序来就行了。

2、中缀表示法

这也就是我们一般的表示法，他的操作符置于操作数的中间（例：1 + 2），前面也说过这种方法不容易被计算机解析，但他符合人们的普遍用法，许多编程语言也就用这种方法了。在中缀表示法中括号是必须有的，要不然运算顺序会乱掉。

3、后缀表示法

后缀表示法又叫逆波兰表示法，他的操作符置于操作数的后面（例：1 2 +），他和前缀表示法都对计算机比较友好，但他很容易用堆栈解析，所以在计算机中用的很多。

他的解释过程一般是：操作数入栈；遇到操作符时，操作数出栈，求值，将结果入栈；当一遍后，栈顶就是表达式的值。因此逆波兰表达式的求值使用堆栈结构很容易实现，且能很快求值。

注意：逆波兰记法并不是简单的波兰表达式的反转。因为对于不满足交换律的操作符，它的操作数写法仍然是常规顺序，如，波兰记法/ 6 3的逆波兰记法是6 3 /而不是3 6 /；数字的数位写法也是常规顺序。

4、表示法间转化

这里介绍一种简单的中缀表达式转化前后缀表达式的方法，比如这个式子：a+b*c-(d+e)

1.按照运算符的优先级对所有的运算单位加括号，式子变成：((a+(b*c))-(d+e))
2.前缀表达式，把运算符号移动到对应的括号前面，式子变成：-(+(a*(bc))+(de))，去掉括号：-+a*bc+de
3.后缀表达式，把运算符号移动到对应的括号后面，式子变成：((a(bc)*)+(de)+)-，去掉括号：abc*+de+-

下面的实例方法与上面的有所不同，因为情况更复杂了，请仔细推敲！

二、实例讲解

1、表达式转换

将以下中缀表达式：

3+4*2/(5-3)^2+3*(4-2)
COS(900-3*10*30)+123.45+30*30-0.45+TAN(0)

转化为后缀表达式(RPN)：

3,4,2,*,5,3,-,2,^,/,+,3,4,2,-,*,+
900,3,10,*,30,*,-,COS,123.45,+,30,30,*,+,0.45,-,0,TAN,+,

2、程序效果

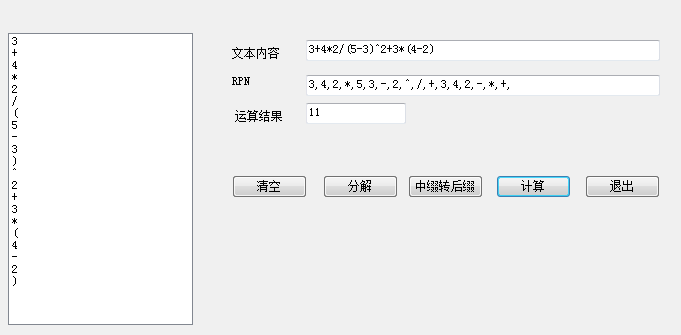
3、编码分析

编码工作主要分为以下几块：

1. 含有函数的中缀表达式转后缀表达式
   • 区分数字、函数名、运算符；
   • 将字符串拆分为数组形式，方便入栈；
   • 判断运算符、函数的优先级，正确排列顺序；
2. 针对后缀表达式进行计算
   • 区分数字、函数名、运算符的不同操作；
   • 根据运算规则不同进行入栈、出栈和计算；

4、转换流程

1. 简单算术表达式的中缀转后缀

1. 带有函数名的表达式，中缀转后缀

5、计算流程

1. 简单算术后缀表达式计算

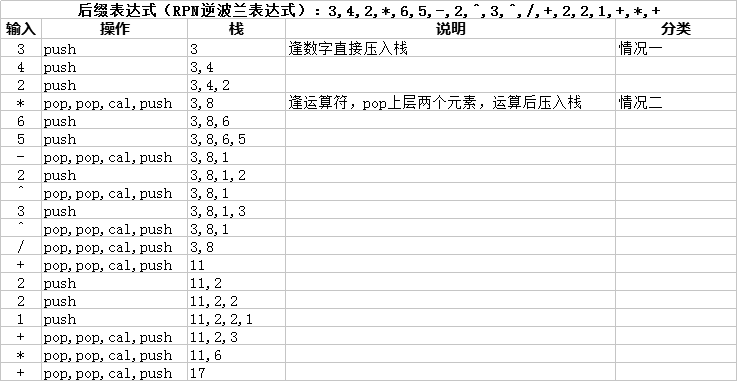
1. 带有函数名的后缀表达式计算

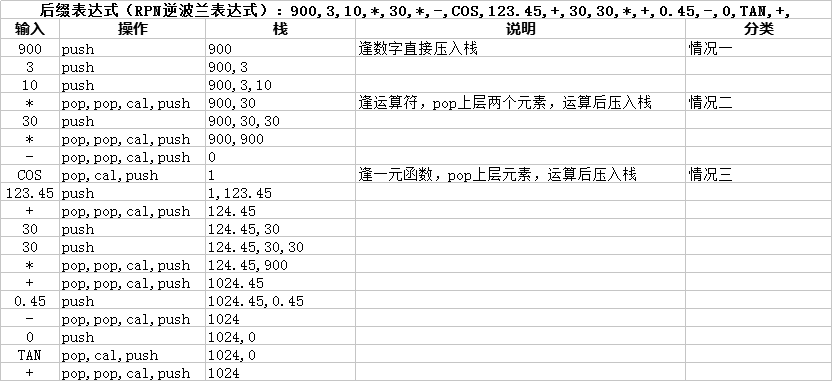
6、实现代码

/*是否为纯数字。正则表达式实现*/
public static bool isNumber(string tmp)
{
    return Regex.IsMatch(tmp, @"[0-9]+[.]{0,1}[0-9]*");
}

/*是否为需拆分的运算符+-*^/() */
public static bool isOp(string tmp)
{
    bool bRet = false;
    switch (tmp)
    {
        case "+":
        case "-":
        case "*":
        case "/":
        case "^":
        case "(":
        case ")":
            bRet = true;
            break;
        default:
            bRet = false;
            break;
    }
    return bRet;
}

/*是否为一元函数名*/
public static bool isFunc(string tmp)
{
    bool bRet = false;
    switch (tmp)
    {
        case "SIN":
        case "COS":
        case "TAN":
        case "SQRT":
            bRet = true;
            break;
        default:
            bRet = false;
            break;
    }
    return bRet;
} 

/*比较运算符及函数优先级。函数视作运算符进行操作。
返回值：1 表示 大于，-1 表示 小于，0 表示 相等    */
public static int compOper(string op1, string op2)
{
    int iRet = 0;
    Dictionary<string, int> dic = new Dictionary<string, int>();
    dic.Add("+", 1);
    dic.Add("-", 1);
    dic.Add("*", 2);
    dic.Add("/", 2);
    dic.Add("^", 3);
    dic.Add("SIN", 4);
    dic.Add("COS", 4);
    dic.Add("TAN", 4);
    dic.Add("SQRT", 4);
    dic.Add("(", 100);
    dic.Add(")", 100);
    if (dic[op1] > dic[op2])
        iRet = 1;
    else if (dic[op1] < dic[op2])
        iRet = -1;
    else
        iRet = 0;
    return iRet;
} 

/*运算符、函数求值*/
public static double calValue(string op, string val1, string val2)
{
    double dRet = 0.0d;
    switch (op)
    {
        case "+":
            dRet = double.Parse(val1) + double.Parse(val2);
            break;
        case "-":
            dRet = double.Parse(val1) - double.Parse(val2);
            break;
        case "*":
            dRet = double.Parse(val1) * double.Parse(val2);
            break;
        case "/":
            if (double.Parse(val2) != 0)
                dRet = double.Parse(val1) / double.Parse(val2);
            else
                MessageBox.Show("Error!");
            break;
        case "^":
            dRet = Math.Pow(double.Parse(val1), double.Parse(val2));
            break;
        default:
            break;
    }
    return dRet;
}

public static double calValue(string op, string val1)
{
    double dRet = 0.0d;
    switch (op)
    {
        case "SIN":
            dRet = Math.Sin(double.Parse(val1));
            break;
        case "COS":
            dRet = Math.Cos(double.Parse(val1));
            break;
        case "TAN":
            dRet = Math.Tan(double.Parse(val1));
            break;
        case "SQRT":
            if (double.Parse(val1) > 0)
                dRet = Math.Sqrt(double.Parse(val1));
            else
                MessageBox.Show("Error!");
            break;
        default:
            break;
    }
    return dRet;
} 

/*按照=+-*^/()分隔出元素*/
public static string splitFunc(string tmp)
{
    string sRet = tmp;
    sRet = sRet.Replace("=", "\n=\n");
    sRet = sRet.Replace("+", "\n+\n");
    sRet = sRet.Replace("-", "\n-\n");
    sRet = sRet.Replace("*", "\n*\n");
    sRet = sRet.Replace("/", "\n/\n");
    sRet = sRet.Replace("^", "\n^\n");
    sRet = sRet.Replace("(", "\n(\n");
    sRet = sRet.Replace(")", "\n)\n");
    return sRet;
}

/*中缀表达式转后缀表达式。tmp为已经添加分隔符的中缀表达式字符串*/
public static string midToRPN(string tmp)
{
    string sRet = "";                                               //返回值
    string[] strArr = splitFunc(tmp.ToUpper()).Split('\n');         //字符串数组，存放分隔后的中缀表达式元素
    Stack<string> strStk = new Stack<string>();                     //栈，用于临时存放运算符和函数名
    for (int i = 0; i < strArr.Length; i++)
    {
        if (string.IsNullOrEmpty(strArr[i]))                        //分隔后为空的元素剔除
            continue;
        else if (calString.isNumber(strArr[i]))                     //纯数字直接入队列
            sRet += strArr[i] + ',';
        else if (calString.isFunc(strArr[i]))                       //一元函数名直接入栈
            strStk.Push(strArr[i]);
        else if (calString.isOp(strArr[i]))                         //运算符特殊处理
        {
            if (strStk.Count != 0 && strStk.Peek() == "(" && strArr[i] != ")")      //栈不为空，最上层为"("，则运算符直接入栈
            {
                strStk.Push(strArr[i]);
            }
            else if (strStk.Count != 0 && strArr[i] == ")")                         //栈不为空，遇")"则pop至"("为止
            {
                while (strStk.Peek() != "(")
                    sRet += strStk.Pop() + ',';
                strStk.Pop();
                if (strStk.Count != 0 && calString.isFunc(strStk.Peek()))           //若"("后为一元函数名，则函数名也pop出
                    sRet += strStk.Pop() + ',';
            }
            else if (strStk.Count != 0 && calString.compOper(strArr[i], strStk.Peek()) == -1)
            {                                                                       //栈不为空，运算符优先级小
                while (strStk.Count != 0 && strStk.Peek() != "(" && calString.compOper(strArr[i], strStk.Peek()) == -1)
                    sRet += strStk.Pop() + ',';                                     //则一直pop【存疑】
                if (strStk.Count != 0)                                              //pop至优先级不小于栈顶运算符则交换位置
                    sRet += strStk.Pop() + ',';                                     //先pop
                strStk.Push(strArr[i]);                                             //再push
            }
            else if (strStk.Count != 0 && calString.compOper(strArr[i], strStk.Peek()) == 0)
            {                                                                       //运算符优先级相同，先pop再push
                sRet += strStk.Pop() + ',';
                strStk.Push(strArr[i]);
            }
            else if (strStk.Count != 0 && calString.compOper(strArr[i], strStk.Peek()) == 1)
            {                                                                       //运算符优先级大，直接入栈
                strStk.Push(strArr[i]);
            }
            else                                                                    //其他情况，入栈【存疑】
            {
                strStk.Push(strArr[i]);
            }
        }
    }
    while (strStk.Count > 0)                //最后栈内元素全部pop出
    {
        sRet += strStk.Pop() + ',';
    }
    return sRet;                            //返回后缀表达式
}

/*根据传入的后缀表达式，求值。tmp为含逗号分隔符的后缀表达式 */
public static double calRPN(string tmp)
{
    double dRet = 0.0d;
    string[] strArr = tmp.Split(',');
    Stack<string> strStk = new Stack<string>();
    for (int i = 0; i < strArr.Length - 1; i++)
    {
        if (isNumber(strArr[i]))                //纯数字入栈
            strStk.Push(strArr[i]);
        else if (isOp(strArr[i]))               //二元运算符，pop两个元素，计算值后压入栈
            strStk.Push(calValue(strStk.Pop(), strStk.Pop(), strArr[i]).ToString());
        else if (isFunc(strArr[i]))         //一元函数名，pop一个元素，计算后压入栈
            strStk.Push(calValue(strArr[i], strStk.Pop()).ToString());
    }
    dRet = double.Parse(strStk.Pop());          //取最后栈中元素作为结果值
    return dRet;
}

/*调用部分代码*/
private void btnTrans_Click(object sender, EventArgs e)
{
    //中缀表达式转后缀表达式
    this.tbRPN.Text = calString.midToRPN(this.tbOrigin.Text);
}

private void btnCal_Click(object sender, EventArgs e)
{
    //后缀表达式求值
    double tmp;
    try
    {
        tmp = calString.calRPN(this.tbRPN.Text);
        this.tbRes.Text = tmp.ToString();
    }
    catch (Exception ex)
    {
        MessageBox.Show(ex.ToString());
        this.tbRes.Text = "Error";
    }
    finally
    {
    }
}