2019南京区域赛ABCHJK题解 & KM-bfs(O(n^3))板子
A.Hard Problem
题目大意:给你一个数n,然后让你计算一个子集大小,这个大小的子集要保证一定存在一个数是另一个数的约数,求出这个最小的数。
做法:显然后面的\(\frac{n}{2}\)个数是互相不为约数的。然后细节再随便搞一搞就行,可以发现\(ans=\lceil\frac{n}{2}\rceil+1\)。
#include<bits/stdc++.h>
using namespace std;
int n,t;
int main(){
scanf("%d",&t);
for(int i=1;i<=t;i++){
scanf("%d",&n);
printf("%d\n",(n+1)/2+1);
}
return 0;
}
B. Chessboard
题目大意:给你棋盘的大小n,m。你需要求出有多少种遍历方式可以遍历整个棋盘,但是在遍历过程中有限制:你不能让你涂完色的格子与其他涂完色的格子在涂色的格子上的最短距离变得更短。
做法:(以下直接抄的别人blog)
首先,我们可以观察到如下几个不难证明的性质:
- 两个被染上颜色的格子之间的距离始终为:曼哈顿距离。
- 一个染色方案是合法的,当且仅当:任何时刻,每行/列被染色的格子要么不存在,要么是连续的一段。
- 如果当前被染色的区域是个矩形,那么最后一个被染色的点,一定在角上。
如果当前被染色的区域是个\(r(r>=2)\)行\(c(c>=2)\)列的矩形,那么接下来要么扩充成 r+1 行 c 列的矩阵(扩充行),要么扩充成 r 行 c+1 列的矩形(扩充列)。并且根据当前状态中最后一个被染色的格子在哪个角上,扩充行/列的方案都是唯一的。
从 1∗1 的矩阵,到 n∗m 的矩阵,一共要扩充 n+m−2 次,其中有 n−1 次是扩充行,这样的决策有 \(C_{n+m-2}^{n-1}\) 种,又由于 1*1 时候的矩阵可以视为左上/右上/左下/右下角,答案需要乘以4.
所以最终答案为\(4C_{n+m-2}^{n-1}\)
具体做法只需要预处理阶乘,然后直接套组合数原始公式+用快速幂求逆即可。
小心\(n=1\)和\(m=1\)的情况。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define IL inline
typedef long long LL;
const int N = 2e6 + 3;
const LL mod = 1e9 + 7;
LL jc[N];
IL void init() {
jc[0] = 1;
for(int i=1;i<=2e6;i++) {
jc[i] = jc[i-1]*i%mod;
}
}
IL LL ksm(LL a,LL b,LL p) {
LL res = 1LL;
while(b) {
if(b&1LL) res = res * a % p;
a = a * a % p;
b >>= 1LL;
}
return res;
}
IL LL C(LL n,LL m,LL p) {
if(n < m) return 0;
return jc[n]*ksm(jc[m],p-2,p)%p*ksm(jc[n-m],p-2,p) % p;
}
int main() {
init();
int T; scanf("%d",&T);
while(T--) {
LL n,m; scanf("%lld%lld",&n,&m);
if(n == 1) {
if(m == 1) printf("1\n");
else printf("2\n");
continue;
}
if(m == 1) {
if(n == 1) printf("1\n");
else printf("2\n");
continue;
}
printf("%lld\n",4LL*C(n+m-2,n-1,mod)%mod);
}
return 0;
}
C. Digital Path
题目大意:你需要找出单调递增1且长度不小于4的路径有多少条。
做法:队友做的。我觉得就是个大模拟Orz。
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
const int MOD = 1e9 + 7;
const int addx[] = {-1, 0, 1, 0};
const int addy[] = {0, 1, 0, -1};
int a[N][N];
int f[N][N][4];
struct Point {
int x, y, a;
}P[1000005];
bool cmp(Point A, Point B) {
return A.a < B.a;
}
int main() {
//freopen("1.txt", "r", stdin);
int n, m;
scanf("%d%d", &n, &m);
int t = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
scanf("%d", &a[i][j]);
P[++t] = (Point) {i, j, a[i][j]};
}
sort(P + 1, P + t + 1, cmp);
for (int i = 1; i <= t; i++) {
int x = P[i].x, y = P[i].y;
for (int j = 0; j < 4; j++) {//四个方向
int fx = x + addx[j], fy = y + addy[j];
if (fx >= 1 && fx <= n && fy >= 1 && fy <= m && a[fx][fy] + 1 == a[x][y]) {
for (int k = 1; k < 4; k++) {
f[x][y][k] = (f[x][y][k] + f[fx][fy][k - 1]) % MOD;
}
f[x][y][3] = (f[x][y][3] + f[fx][fy][3]) % MOD;
}
}
if (f[x][y][1] == 0 && f[x][y][2] == 0 && f[x][y][3] == 0)
f[x][y][0] = 1;
}
int ans = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
int pd = 1;
for (int k = 0; k < 4; k++) {
int x = i + addx[k], y = j + addy[k];
if (x >= 1 && x <= n && y >= 1 && y <= m && a[x][y] == a[i][j] + 1) pd = 0;
}
if (pd)
ans = (ans + f[i][j][3]) % MOD;
}
printf("%d", ans);
return 0;
}
H.Prince and Princess
大意:王子要找到公主在哪个房间。有三类人,说真话的(包括公主),不说真话的,随便人。给你这三种人各自的人数a,b,c,你需要判断你最少需要问多少人才能问出来公主在哪个房间。
做法:显然当\(a>b+c\)时你就能问出来公主在哪,问的次数也显然是\(2(b+c)+1\),不过要小心\(1,0,0\)的情况应该输出0.
#include <bits/stdc++.h>
using namespace std;
int main() {
int a, b, c;
cin >> a >> b >> c;
if (a > b + c) {
if (a == 1 && b == 0 && c == 0)
printf("YES\n0");
else
printf("YES\n%d", (b + c) * 2 + 1);
}
else
printf("NO\n");
return 0;
}
J. Spy
大意:你需要给你的人配对,两人配成一对击败对面的队伍获得一定的名声值,你要求出最大的期望名声*n。
做法:假如此时你已经把所有人都配对好了,设此时你每个队队伍的力量值为\(d_i\),那么最后答案为$$ans=\sum_{i=1}n\sum_{j=1}n[d_i<a_j]p_j$$
我们可以发现配对的过程是一个二分图最大权匹配。边权就是\(b_i\)与\(c_j\)相连对答案的贡献$$\sum_{k=1}^n[b_i+c_j>a_k]p_k$$
然后这个题把(在我已知范围内的)除了bfs的\(O(n^3)\)以外的所有算法都给卡了。包括我写dfs的\(O(n^3)\)算法也过不去,甚至dfs的\(O(n^4)\)算法比\(O(n^3)\)还快。
这个板子需要记录一下,因为我不会写。
bfs ac。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define IL inline
typedef long long LL;
const int N = 400 + 3;
const int INF = 0x3f3f3f3f;
struct Kuhn_Munkers {
int n;
int W[N][N];
int Lx[N],Ly[N];
int left[N];
int slack[N];
int pre[N];
bool T[N];
IL void init(int n) {
this->n = n;
for(int i=1;i<=n;i++) fill(W[i],W[i]+1+n,INF);
}
IL void bfs(int u) {
fill(slack,slack+1+n,INF);
fill(pre,pre+1+n,0);
int x,y=0,yy=0,a;
left[y] = u;
for(;;) {
x = left[y]; a = INF, T[y] = true;
for(int i=1;i<=n;i++) if(!T[i]){
if(slack[i] > Lx[x]+Ly[i]-W[x][i]) {
slack[i] = Lx[x] + Ly[i] - W[x][i];
pre[i] = y;
}
if(slack[i] < a) a = slack[i],yy = i;
}
for(int i=0;i<=n;i++) {
if(T[i]) { Lx[left[i]] -= a; Ly[i] += a;}
else slack[i] -= a;
}
y = yy;
if(!left[y]) break;
}
while(y) left[y] = left[pre[y]], y = pre[y];
}
IL int KM() {
fill(Lx,Lx+1+n,0);
fill(Ly,Ly+1+n,0);
fill(left,left+1+n,0);
for(int i=1;i<=n;i++) {
fill(T,T+1+n,false);
bfs(i);
}
int ans = 0LL;
for(int j=1;j<=n;j++) ans += W[left[j]][j];
return ans;
}
}solver;
int n;
int p[N];
LL a[N],b[N],c[N];
int main() {
scanf("%d",&n); solver.init(n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<=n;i++) scanf("%d",&p[i]);
for(int i=1;i<=n;i++) scanf("%lld",&b[i]);
for(int i=1;i<=n;i++) scanf("%lld",&c[i]);
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) {
int v = 0;
for(int k=1;k<=n;k++) if(b[i]+c[j] > a[k]) v += p[k];
solver.W[i][j] = v;
}
}
printf("%d\n",solver.KM());
return 0;
}
dfs tle
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define IL inline
typedef long long LL;
const int N = 400 + 3;
const int INF = 0x3f3f3f3f;
struct Kuhn_Munkers {
int n;
int W[N][N];
int Lx[N],Ly[N];
int left[N];
int slack[N];
bool S[N],T[N];
IL void init(int n) {
this->n = n;
for(int i=1;i<=n;i++) fill(W[i],W[i]+1+n,INF);
fill(Lx,Lx+1+n,0);
fill(Ly,Ly+1+n,0);
fill(left,left+1+n,0);
}
bool match(int i) {
S[i] = true;
for(int j=1;j<=n;j++) if(!T[j]) {
if(Lx[i]+Ly[j] == W[i][j]) {
T[j] = true;
if(!left[j] || match(left[j])) {
left[j] = i;
return true;
}
}
else slack[j] = min(slack[j],Lx[i]+Ly[j]-W[i][j]);
}
return false;
}
IL void update() {
int a = INF;
for(int j=1;j<=n;j++) if(!T[j]) a = min(a,slack[j]);
for(int i=1;i<=n;i++) {
if(S[i]) Lx[i] -= a;
if(T[i]) Ly[i] += a;
else slack[i] -= a;
}
}
IL int KM() {
for(int i=1;i<=n;i++) {
left[i] = Lx[i] = Ly[i] = 0;
for(int j=1;j<=n;j++)
Lx[i] = max(Lx[i],W[i][j]);
}
for(int i=1;i<=n;i++) {
fill(slack,slack+1+n,INF);
for(;;) {
for(int j=1;j<=n;j++) S[j]=T[j]=0;
if(match(i)) break; else update();
}
}
int ans = 0LL;
for(int j=1;j<=n;j++) {
ans += W[left[j]][j];
}
return ans;
}
}solver;
int n;
int p[N];
LL a[N],b[N],c[N];
int main() {
scanf("%d",&n); solver.init(n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<=n;i++) scanf("%d",&p[i]);
for(int i=1;i<=n;i++) scanf("%lld",&b[i]);
for(int i=1;i<=n;i++) scanf("%lld",&c[i]);
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) {
int v = 0;
for(int k=1;k<=n;k++) if(b[i]+c[j] > a[k]) v += p[k];
solver.W[i][j] = v;
}
}
printf("%d\n",solver.KM());
return 0;
}
K.Triangle
大意:给你一个三角形,你需要找到一条线段平分这个三角形的面积,这个线段的一个端点已经给出了。
做法:简单的计算几何题,但是我写了3.5kb,非常难受。
给的端点如果不在三角形边上或者角上直接输出-1.
那么在三角形边上可以分成两种情况:
- 给的端点在角上。
- 给的端点在边上。
如果给的端点在角上,那么显然你只需要输出对边的中点即可。
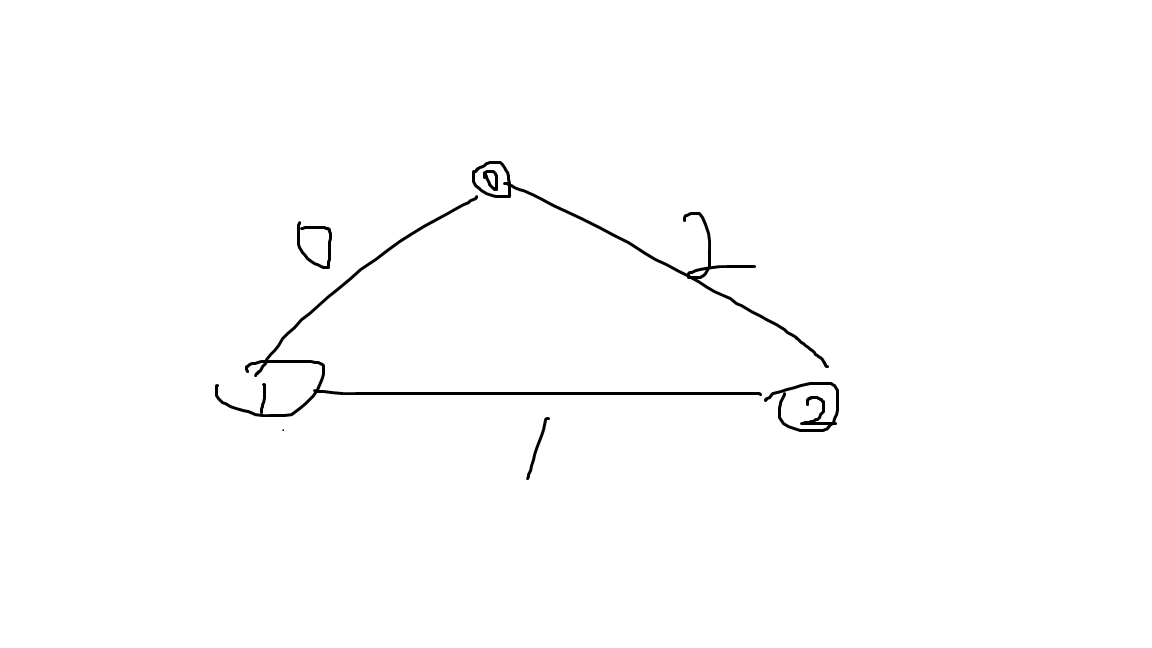
如果给的端点在边上,那么你可以枚举这个端点相邻的两个角,然后利用正弦的面积公式,得出另一个端点在哪里,如果另一个端点不在三角形上就不要它。
配一张图,看一下我的代码里边和角的命名。
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<vector>
#include<algorithm>
using namespace std;
#define IL inline
typedef long long LL;
const double PI = acos(-1.0);
const double eps = 1e-10;
struct Point {
double x,y;
IL Point() {}
IL Point(double x,double y):x(x),y(y){}
};
typedef Point Vector;
IL Vector operator + (const Vector& A,const Vector& B) { return Vector(A.x+B.x,A.y+B.y);}
IL Vector operator - (const Vector& A,const Vector& B) { return Vector(A.x-B.x,A.y-B.y);}
IL Vector operator * (const Vector& A,double p) { return Vector(A.x*p,A.y*p);}
IL Vector operator / (const Vector& A,double p) { return Vector(A.x/p,A.y/p);}
IL bool operator < (const Point& a, const Point& b) { return a.x < b.x || (a.x == b.x && a.y < b.y);}
IL int dcmp(double x) { if(fabs(x) < eps) return 0; else return x < 0 ? -1 : 1;}
IL bool operator == (const Point& A,const Point& B) { return dcmp(A.x-B.x) == 0 && dcmp(A.y-B.y) == 0;}
IL double Dot(const Vector& A,const Vector& B) { return A.x*B.x + A.y*B.y;}
IL double Length(const Vector& A) { return sqrt(Dot(A,A));}
IL double Angle(const Vector& A,const Vector& B) { return acos(Dot(A,B) / Length(A) / Length(B));}
IL double Cross(const Vector& A,const Vector& B) { return A.x*B.y - A.y*B.x;}
IL double Area2(const Point& A, const Point& B,const Point& C) { return Cross(B-A,C-A);}
IL Vector Rotate(const Vector& A,double rad) { return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));}
IL Vector Normal(const Vector& A) { double L = Length(A); return Vector(-A.y/L,-A.x/L);}
IL double DistanceToSegment(const Point& P,const Point& A,const Point& B) {
if(A == B) return Length(P-A);
Vector v1 = B-A, v2 = P-A, v3 = P-B;
if(dcmp(Dot(v1,v2)) < 0) return Length(v2);
else if(dcmp(Dot(v1,v3)) > 0) return Length(v3);
else return fabs(Cross(v1,v2)) / Length(v1);
}
int vtos[5][5];
int stov[5][5];
IL void init() {
vtos[0][1] = vtos[1][0] = 0;
vtos[0][2] = vtos[2][0] = 2;
vtos[1][2] = vtos[2][1] = 1;
stov[0][0] = 0; stov[0][1] = 1;
stov[1][0] = 1; stov[1][1] = 2;
stov[2][0] = 0; stov[2][1] = 2;
}
bool may[5];
IL int valid(Point* p) {
may[0]=may[1]=may[2] = false;
for(int i=0;i<3;i++) if(p[i] == p[3]) {
may[(i+1)%3] = true; return 1;
}
for(int i=0;i<3;i++) {
for(int j=0;j<i;j++) {
if(DistanceToSegment(p[3],p[i],p[j]) == 0) {
may[0]=may[1]=may[2] = true;
may[vtos[i][j]] = false;
return 2;
}
}
}
return 0;
}
IL void EndPoint_On_Vertices(Point* p) {
int now;
for(int i=0;i<3;i++) if(may[i]) now = i;
Point a = p[stov[now][0]] , b = p[stov[now][1]];
Point ans = a + (b-a) / 2.0;
printf("%lf %lf\n",ans.x,ans.y);
}
IL void EndPoint_On_Sides(Point *p) {
int pos;
for(int i=0;i<3;i++) if(!may[i]){ pos = i;}
for(int i=0;i<2;i++) {
int v1 = stov[pos][i], v2 = stov[pos][i^1], v3 = 3-v1-v2;
double S = Length(p[v2]-p[v1]) / 2.0 *Length(p[v3]-p[v1]);
double d = S / Length(p[3]-p[v1]);
Point ans = p[v1] + (p[v3]-p[v1]) / Length(p[v3]-p[v1]) * d;
if(DistanceToSegment(ans,p[v1],p[v3]) > eps) continue;
printf("%lf %lf\n",ans.x,ans.y); return;
}
printf("-1\n");
}
Point p[10];
int main() {
int T; scanf("%d",&T); init();
while(T--) {
for(int i=0;i<4;i++) {
int x,y; scanf("%d%d",&x,&y);
p[i] = Point(x,y);
}
int d = valid(p);
if(!d) { printf("-1\n"); continue;}
else if(d == 1) EndPoint_On_Vertices(p);
else EndPoint_On_Sides(p);
}
return 0;
}
后面随便复制粘贴一些别人博客我没写的题解。

2019南京区域赛ABCHJK题解 & KM-bfs(O(n^3))板子的更多相关文章
- 【2013南京区域赛】部分题解 hdu4802—4812
上周末打了一场训练赛,题目是13年南京区域赛的 这场题目有好几个本来应该是我擅长的,但是可能是太久没做比赛了各种小错误代码写的也丑各种warusn trush搞得人很不爽 全场题之一的1002也没有想 ...
- 2019 南京网络赛A
南京网络赛自闭现场 https://nanti.jisuanke.com/t/41298 二维偏序经典题型 二维前缀和!!! #include<bits/stdc++.h> using n ...
- 2018 ACM-ICPC南京区域赛题解
解题过程 开场开A,A题shl看错题意,被制止.然后开始手推A,此时byf看错E题题意,开始上机.推出A的规律后,shl看了E题,发现题意读错.写完A题,忘记判断N=0的情况,WA+1.过了A后,sh ...
- The Preliminary Contest for ICPC Asia Nanjing 2019/2019南京网络赛——题解
(施工中……已更新DF) 比赛传送门:https://www.jisuanke.com/contest/3004 D. Robots(期望dp) 题意 给一个DAG,保证入度为$0$的点只有$1$,出 ...
- 2017沈阳区域赛Infinite Fraction Path(BFS + 剪枝)
Infinite Fraction Path Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 262144/262144 K (Java ...
- 2018ACM-ICPC南京区域赛M---Mediocre String Problem【exKMP】【Manacher】
这题就单独写个题解吧.想了两天了,刚刚问了一个大佬思路基本上有了. 题意: 一个串$S$,一个串$T$,在$S$中选一段子串$S[i,j]$,在$T$中选一段前缀$T[1,k]$使得$S[i,j]T[ ...
- 2018ACM-ICPC南京区域赛---AJGIDKM
含[最小球覆盖][最大流isap]模板. 题面pdf https://codeforc.es/gym/101981/attachments/download/7891/20182019-acmicpc ...
- 2018-2019 ACM-ICPC 徐州区域赛 部分题解
题目链接:2018-2019 ACM-ICPC, Asia Xuzhou Regional Contest A. Rikka with Minimum Spanning Trees 题意: 给出一个随 ...
- 2018南京区域赛K题 Kangaroo Puzzle——随机&&乱搞
题意 在 n * m 的平面上有若干个袋鼠和墙(1为袋鼠,0为墙),每次可以把所有袋鼠整体往一个方向移动一步(不能走出边界和不能走到墙),为在不超过50000步的情况下能否把全部袋鼠聚集在同一个位置. ...
- Robots 2019南京网络赛 (概率dp)
Robots \[ Time Limit: 1000 ms \quad Memory Limit: 262144 kB \] 题意 有一个机器人要从 \(1\) 点走到 \(n\) 点,每走一步都需要 ...
随机推荐
- 5.prometheus监控--监控nginx
1.监控程序环境准备 mkdir /data/docker-compose -p cd /data/docker-compose cat > docker-compose.yaml <&l ...
- 混合开发中,app内嵌h5页面时,安卓ios遇到的一些兼容问题及解决方法
1.input[type=checkbox]在ios端样式显示异常,黑色背景或边框,安卓正常 解决: input[type=checkbox]:checked{ background-color: t ...
- postman使用中问题汇总
当用postman来通过接口造数据时,读取参数化文件中身份证字段的值读取错误. 参数文件如下 选择参数文件后预览的数据如下 身份证号码全部变成了0000结尾的 解决方案: 需要将身份证号码用引号引起来 ...
- 如何使用go module导入本地包
go module是Go1.11版本之后官方推出的版本管理工具,并且从Go1.13版本开始,go module将是Go语言默认的依赖管理工具. 到今天Go1.14版本推出之后Go modules 功能 ...
- 逆向wechat
本篇博客园地址https://www.cnblogs.com/bbqzsl/p/18171552 计划来个wechat的逆向系列,包括主程序WeChat,以及小程序RadiumWMPF. 开篇,对We ...
- 2022年官网下安装ZooKeeper最全版与官网查阅方法
目录 一.环境整合 构建工具(参考工具部署方式) 二.官网下载 三.解压安装 四.配置环境 五.启动运行 六.配置为服务 七.查看设置服务 其他版本安装 构建工具(参考工具部署方式) 一.环境整合 构 ...
- MAC Pro 同时安装 Python2 和 Python3
目录 文章目录 目录 安装 Python2 安装 Python3 不同版本Python路径 配置 Python2 和 Python3 安装 Python2 MAC 系统已经默认带有 Python2.7 ...
- pageoffice 6 实现pdf加盖印章和签字功能
PageOffice支持两种电子印章方案,可实现对Word.Excel.PDF文档加盖PageOffice自带印章或ZoomSeal电子印章(全方位保护.防篡改.防伪造).Word和Excel的盖章功 ...
- kubernetes 之二进制方式部署
我的资料链接:https://pan.baidu.com/s/18g0sar1N-FMhzY-FCMqOog 两种集群架构图 多master需要在集群上面加个lb,所有的node都需要连接lb,lb帮 ...
- Docker 必知必会4----容器之间的通信
前面几篇文章,我们基本聊了docker的基本概念,以及基本的操作手段: https://www.cnblogs.com/jilodream/p/18177695 初识dockerhttps://w ...
