SSL新年欢乐赛暨BPM退役赛(不含FK)

目录

• 前言
• C 大水题
  • 题目
  • 分析
  • 代码
• D 简单数据结构题
  • 题目
  • 分析
  • 代码
• H 上次题
  • 题目
  • 分析
  • 代码
• J 白给题
  • 题目
  • 分析
  • 代码

前言

A,B水题，E,I原题

实际赛时400分（乐多毁我青春）

G题改完了，看这篇吧

---

C 大水题

题目

如果有一个长度为\(n\)的数组\(a[1],a[2],\cdots,a[n]\)，对于非负整数\(k\)，若令\(b[i]=a[i] \oplus k\)，满足bb是一个单调不下降的数组，即满足\(b[1]\le b[2]\le \cdots \le b[n]\)，则称\(k\)是数组\(a\)的完美数，其中\(\oplus\)表示按位异或。

现在给出一个长度为\(n\)的数组\(a\)，并进行\(q\)次修改，每次会改变\(a\)中的一个数。要求在第一次修改前以及每一次修改后求出当前数组的最小完美数，若不存在则输出\(-1\)。

---

分析

从局部到整体考虑，如果相邻两个数\(x,y\)，改变这两个数大小关系当且仅当一个二进制位是0一个是1的最高位被改变，那么可以用两个数组表示某个位置是否必然改变或必然不改变，累加次数，它待修改就先减掉再加上修改后的情况，如果两个数组的某一位都大于0，那么必然输出\(-1\),接着只要必然修改的位置数组大于0，那么就必须要让这一位变成1，时间复杂度\(O(30(n+q))\)

---

代码

#include <cstdio>
#include <cctype>
#define rr register
using namespace std;
int n,a[1000011],ac[31],wa[31];
inline signed iut(){
	rr int ans=0; rr char c=getchar();
	while (!isdigit(c)) c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
inline signed get_top(int x){
	for (rr int i=30;~i;--i)
	    if ((x>>i)&1) return i;
	return -1;
}
inline void Add(int x){
	rr int t=get_top(a[x]^a[x+1]);
	if (t==-1) return;
	if (a[x]<=a[x+1]) ++ac[t]; else ++wa[t];
}
inline void Del(int x){
	rr int t=get_top(a[x]^a[x+1]);
	if (t==-1) return;
	if (a[x]<=a[x+1]) --ac[t]; else --wa[t];
}
inline bool check(){
	for (rr int i=30;~i;--i)
	if (ac[i]&&wa[i]) return 0;
	return 1;
}
inline void print(int ans){
	if (ans>9) print(ans/10);
	putchar(ans%10+48);
}
inline void doit(){
	if (check()){
		rr int sum=0;
		for (rr int i=30;~i;--i)
		if (wa[i]) sum|=1<<i;
		print(sum);
	}else putchar('-'),putchar(49);
}
signed main(){
	n=iut();
	for (rr int i=1;i<=n;++i) a[i]=iut();
	for (rr int i=1;i<n;++i) Add(i);
	doit();
	for (rr int Q=iut();Q;--Q){
		rr int x=iut(),y=iut();
		if (x>1) Del(x-1);
		if (x<n) Del(x);
		a[x]=y;
		if (x>1) Add(x-1);
		if (x<n) Add(x);
		putchar(10); doit();
	}
	return 0;
}

---

D 简单数据结构题

题目

对于一个长度为\(n\)的序列\(a_1,a_2,\cdots,a_n\)，找一个整数\(k\)使得\(\max\limits_{1\le i\le n}(a_i\oplus k)\)尽可能小，其中\(\oplus\)表示按位异或。

样例输入：3 1 2 3 样例输出：2

---

分析

首先数据结构要确定，选择\(\text{Trie}\),接着建好一个 \(\text{Trie}\)，样例如图所示（简化版）

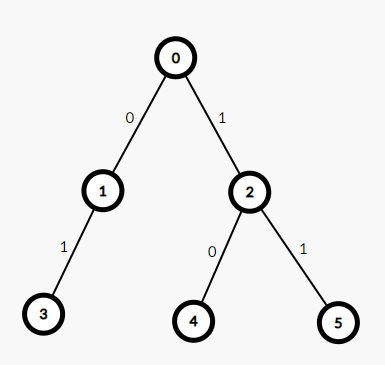
首先这棵树整棵树肯定得用，所以要搜索，如果遇到一个分支怎么办，如果不把这一位变成1，答案肯定会变大，但是这一位变成1，我把它给大的答案肯定得不偿失，所以把小的那一条路这一位变成1，继续跳到上一行

---

代码

#include <cstdio>
#include <cctype>
#include <queue>
#define rr register
using namespace std;
const int N=100001;
int trie[N<<5][2],tot,n,a[N],ans=1<<30;
inline signed iut(){
	rr int ans=0; rr char c=getchar();
	while (!isdigit(c)) c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
inline signed min(int a,int b){return a<b?a:b;}
inline void Insert(int x){
	rr int p=0;
	for (rr int i=29;~i;--i){
		rr int t=(x>>i)&1;
		if (!trie[p][t]) trie[p][t]=++tot;
	    p=trie[p][t];
	}
}
inline signed dfs(int p,int now){
	if (!trie[p][0]&&!trie[p][1]) return 0;
	rr int t,cnt=0;
	if (trie[p][0]) t=dfs(trie[p][0],now-1),++cnt;
	if (trie[p][1]) t=min(t,dfs(trie[p][1],now-1)),++cnt;
	if (cnt==2) t|=1<<now;
	return t;
}
signed main(){
	n=iut();
	for (rr int i=1;i<=n;++i) Insert(a[i]=iut());
	return !printf("%d",dfs(0,29));
}

---

H 上次题

题目

在\(n\)个数中选出若干个分为两部分，使两部分和相等，问其中一部分和的最大值，\(n\)个数的总和\(<5000\)

---

分析

设\(dp[x]\)表示两部分差值为\(x\)的总和，那给出这个定义就很好做了，时间复杂度\(O(n*sum)\)，注意平移下标

---

代码

#include <cstdio>
#include <cctype>
#define rr register
using namespace std;
const int N=1001;
int a[N],dp[2][N*5],n,sum;
inline signed iut(){
    rr int ans=0,f=1; rr char c=getchar();
    while (!isdigit(c)) f=(c=='-')?-f:f,c=getchar();
    while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
    return ans*f;
}
inline signed max(int a,int b){return a>b?a:b;}
signed main(){
    n=iut();
	for (rr int i=1;i<=n;++i) a[i]=iut(),sum+=a[i]; sum=sum-(sum&1);
	for (rr int i=0;i<=sum;++i) dp[0][i]=-2e9; dp[0][sum>>1]=0;
	for (rr int i=1;i<=n;++i){
		for (rr int j=0;j<=sum;++j) dp[i&1][j]=dp[(i&1)^1][j];
		for (rr int j=sum;j>=a[i];--j) dp[i&1][j]=max(dp[(i&1)^1][j-a[i]]+a[i],dp[i&1][j]);
		for (rr int j=a[i];j<=sum;++j) dp[i&1][j-a[i]]=max(dp[(i&1)^1][j]+a[i],dp[i&1][j-a[i]]);
	}
    return !printf("%d",dp[n&1][sum>>1]/2);
}

J 白给题

题目

删除每一条边，两棵子树颜色交集

---

分析

dsu板子题，预处理出总颜色数组就可以了

---

代码

#include <cstdio>
#include <cctype>
#include <cstring>
#define rr register
using namespace std;
const int N=100011;
struct node{int y,next;}e[N<<1];
int root,col[N],hs[N],k=1,n,son[N],cnt[N],ans[N];
int now,dep[N],fat[N],big[N],snt[N],pig[N];
inline signed iut(){
	rr int ans=0; rr char c=getchar();
	while (!isdigit(c)) c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
inline void print(long long ans){
	if (ans>9) print(ans/10);
	putchar(ans%10+48);
}
inline void dfs1(int x,int fa){
	dep[x]=dep[fa]+1,fat[x]=fa,son[x]=1;
	for (rr int i=hs[x],mson=-1;i;i=e[i].next)
	if (e[i].y!=fa){
		dfs1(e[i].y,x);
		son[x]+=son[e[i].y];
		if (son[e[i].y]>mson){
		    big[x]=e[i].y,pig[x]=i,
			mson=son[e[i].y];
		}
	}
}
inline void update(int x,int z){
	if (z==1){
		if (!cnt[col[x]]) now+=snt[col[x]]>1;
		    else now-=snt[col[x]]==1;
	}else{
		if (!snt[col[x]]) now+=cnt[col[x]]>1;
		    else now-=cnt[col[x]]==1;
	}
	cnt[col[x]]+=z,snt[col[x]]-=z;
	for (rr int i=hs[x];i;i=e[i].next)
	if (e[i].y!=fat[x]&&e[i].y!=root) update(e[i].y,z);
}
inline void dfs2(int x,int opt,int p){
	for (rr int i=hs[x];i;i=e[i].next)
	if (e[i].y!=fat[x]&&e[i].y!=big[x]) dfs2(e[i].y,0,i);
	if (big[x]) dfs2(big[x],1,pig[x]),root=big[x];
	update(x,1),ans[p>>1]=now,root=0;
	if (!opt) update(x,-1),now=0;
}
signed main(){
	while (scanf("%d",&n)==1){
		memset(snt,0,sizeof(snt)),memset(cnt,0,sizeof(cnt));
		memset(ans,0,sizeof(ans)),memset(dep,0,sizeof(dep));
		memset(fat,0,sizeof(fat)),memset(son,0,sizeof(son));
		memset(big,0,sizeof(big)),memset(pig,0,sizeof(pig));
		memset(hs,0,sizeof(hs)),k=1;
        for (rr int i=1;i<=n;++i) col[i]=iut(),++snt[col[i]];
        for (rr int i=1;i<n;++i){
    	    rr int x=iut(),y=iut();
    	    e[++k]=(node){y,hs[x]},hs[x]=k,
    	    e[++k]=(node){x,hs[y]},hs[y]=k;
	    }
	    dfs1(1,0),dfs2(1,0,0);
	    for (rr int i=1;i<n;++i)
	        print(ans[i]),putchar(i==n-1?10:32);
	}
	return 0;
}

未完待续