论文解读(Moka‑ADA)《Moka‑ADA: adversarial domain adaptation with model‑oriented knowledge adaptation for cross‑domain sentiment analysis》
Note:[ wechat:Y466551 | 可加勿骚扰,付费咨询 ]
论文信息
论文标题:Moka‑ADA: adversarial domain adaptation with model‑oriented knowledge adaptation for cross‑domain sentiment analysis
论文作者:Maoyuan ZhangXiang LiFei Wu
论文来源:2023 aRxiv
论文地址:download
论文代码:download
视屏讲解:click
1 介绍
出发点:以往方法将特征表示转换为域不变的方法倾向于只对齐边缘分布,并且不可避免地会扭曲包含判别知识的原始特征表示,从而使条件分布不一致;
以往方法和本文方法的对比:我们采用对抗性判别域自适应(ADDA)框架来学习边际分布对齐的领域不变知识,在此基础上,在源模型和目标模型之间进行知识自适应以实现条件分布对齐。具体地说,我们设计了一个对中间特征表示和fnal分类概率具有相似性约束的对偶结构,以便训练中的目标模型从训练后的源模型中学习鉴别知识。在一个公开的情绪分析数据集上的实验结果表明,我们的方法取得了新的最先进的性能。
跨域情绪分析相关工作的联系:
- 伪标记技术[3,4],使用在源标记数据上训练的模型,为未标记的目标数据生成伪标签,然后以监督的方式训练目标域的模型;
- 基于枢轴的方法[5,6],旨在选择域不变的特征,并将它们作为跨域映射的基础;
- 对抗性训练方法[7,8],目的是通过在模型训练过程中添加对抗性代价来学习输入样本的域独立映射,从而使源域分布和目标域分布之间的距离最小化;
方法对比:

研究目的:除了对齐边缘分布,还对齐了类条件分布;
贡献:
- 提出了一种新的方法,Moka-ADA,来学习领域不变知识和判别知识,以确保边缘分布和条件分布同时对齐;
- 设计了一个包含具有相似性约束的对偶结构的面向模型的知识自适应模块,使训练中的目标模型能够从训练后的源模型中学习鉴别性知识;
- 采用知识蒸馏来促进鉴别知识的转移,这有助于增加类间距离,从而减少类内距离,并提高对抗性领域自适应的稳定性;
- 在亚马逊审查基准数据集上进行了广泛的实验,平均准确率为94.25%,将CDSA任务的最新性能提高了1.11%;
2 方法
2.1 Model‑oriented knowledge adaptation
为了使训练中的目标编码器从训练后的源编码器中学习鉴别性知识,设计了一个面向模型的知识自适应模块,包括中间特征表示相似度约束(ISC)和最终分类概率相似度约束(FSC)。
2.1.1 Intermediate similarity constraints (ISC) based on the reproducing kernel hilbert space
源域数据 $\boldsymbol{x}_{s} \sim \mathbb{D}_{S}$,通过源域编码器 $E_{s}$ 和 目标编码器 $E_{t}$ 分别得到特征表示 $\boldsymbol{h}_{s}=E_{s}\left(\boldsymbol{x}_{s}\right)$、 $\hat{\boldsymbol{h}}_{t}=E_{t}\left(\boldsymbol{x}_{s}\right)$,且满足 $\boldsymbol{H}_{S}=\left\{\left(\boldsymbol{h}_{s}^{i}\right)\right\}_{i=1}^{n} \sim \mathbb{H}_{S}$ 和 $\boldsymbol{H}_{T}=\left\{\left(\hat{\boldsymbol{h}}_{t}^{i}\right)\right\}_{i=1}^{n} \sim \mathbb{H}_{T} $,特征分布 $\mathbb{H}_{S}$ 和 $\mathbb{H}_{T}$ 之间的距离使用 $\text{MMD}$ 计算:
$\begin{aligned}\underset{E_{t}}{\text{min}} \; & \mathcal{L}_{\mathrm{ISC}}\left(\boldsymbol{x}_{s}\right) \\= & \operatorname{MMD}^{2}\left[\mathcal{F}, \boldsymbol{h}_{s}, \hat{\boldsymbol{h}}_{t}\right] \\= & \left\|\mathbb{E}_{\boldsymbol{h}_{s} \sim \mathbb{H}_{S}} \phi\left(\boldsymbol{h}_{s}\right)-\mathbb{E}_{\hat{\boldsymbol{h}}_{\boldsymbol{t}} \sim \mathbb{H}_{T}} \phi\left(\hat{\boldsymbol{h}}_{t}\right)\right\|_{\mathcal{H}}^{2} \\= & \mathbb{E}_{\boldsymbol{h}_{s}, \boldsymbol{h}_{s}^{\prime} \sim \mathbb{H}_{s}, \mathbb{H}_{S}} k\left(\boldsymbol{h}_{s}, \boldsymbol{h}_{s}^{\prime}\right) - 2 \mathbb{E}_{\boldsymbol{h}_{s}, \hat{\boldsymbol{h}}_{t} \sim \mathbb{H}_{s}, \mathbb{H}_{T}} k\left(\boldsymbol{h}_{s}, \hat{\boldsymbol{h}}_{t}\right) +\mathbb{E}_{\hat{\boldsymbol{h}}_{t}, \hat{h}_{t}^{\prime} \sim \mathbb{H}_{T}, \mathbb{H}_{T}} k\left(\hat{\boldsymbol{h}}_{t}, \hat{\boldsymbol{h}}_{t}^{\prime}\right),\end{aligned}$
其中,核函数 $k(\boldsymbol{u}, \boldsymbol{v})=\sum_{i=1}^{m} \exp \left\{-\frac{1}{2 \delta_{i}}\|\boldsymbol{u}-\boldsymbol{v}\|_{2}^{2}\right\}$;
2.1.2 Final similarity constraints (FSC) based on the knowledge distillation
传统的方法将对目标样本设置一个硬标签(伪标签),这在重复训练过程中容易造成过拟合。为了缓解这一问题,利用知识蒸馏(KD),通过产生一个软概率分布来控制知识转移的程度。
软概率分布的优势:
- 软标签用多个概率值来描述概率分布,可以更好地处理噪声和不确定性;
- 包含了不同类之间的相关性信息,有助于增加类间距离,从而减少类内距离;
接着将 $\boldsymbol{h}_{s}$、$\hat{\boldsymbol{h}}_{t}$ 放入放缩余弦分类器
$\boldsymbol{p}_{s}=C_{s}\left(\boldsymbol{h}_{s}\right)$ $\hat{\boldsymbol{p}}_{t}=C_{s}\left(\hat{\boldsymbol{h}}_{t}\right)$ $\boldsymbol{P}=\sigma\left(\boldsymbol{p}_{s} / T\right)$ $\boldsymbol{Q}=\sigma\left(\hat{\boldsymbol{p}}_{t} / T\right)$
最终相似性约束如下:
$\begin{aligned}\underset{E_{t}}{\text{min}} \; & \mathcal{L}_{\mathrm{FSC}}\left(\boldsymbol{x}_{s}\right) \\& =T^{2} \cdot \operatorname{KL}(\boldsymbol{P} \| \boldsymbol{Q}) \\& =T^{2} \cdot \mathbb{E}_{\boldsymbol{x}_{s} \sim \mathbb{D}_{S}} \sum_{k=1}^{K} P_{k} \log \frac{P_{k}}{Q_{k}},\end{aligned}$
2.1 节小结:综上所述,对源编码器和目标编码器的输入是相同的,目标编码器用“中间”和“fnal”来模拟源编码器,从而实现条件分布对齐的鉴别知识。
笔记:
传统的余弦相似度计算公式为:
cosine similarity = dot product(A, B) / (norm(A) * norm(B))
其中,dot product(A, B)表示向量 A 和 B 的点积,norm(A) 和 norm(B) 分别表示向量 A 和 B 的范数。
放缩余弦分类器通过引入放缩因子来调整余弦相似度的计算,公式如下:
scaled cosine similarity = dot product(A, B) / (scale_factor * norm(A) * norm(B))
2.2 Adversarial domain adaptation with model‑oriented knowledge adaptation
本文提出的 Moka-ADA 框架 如 Figure2 所示:
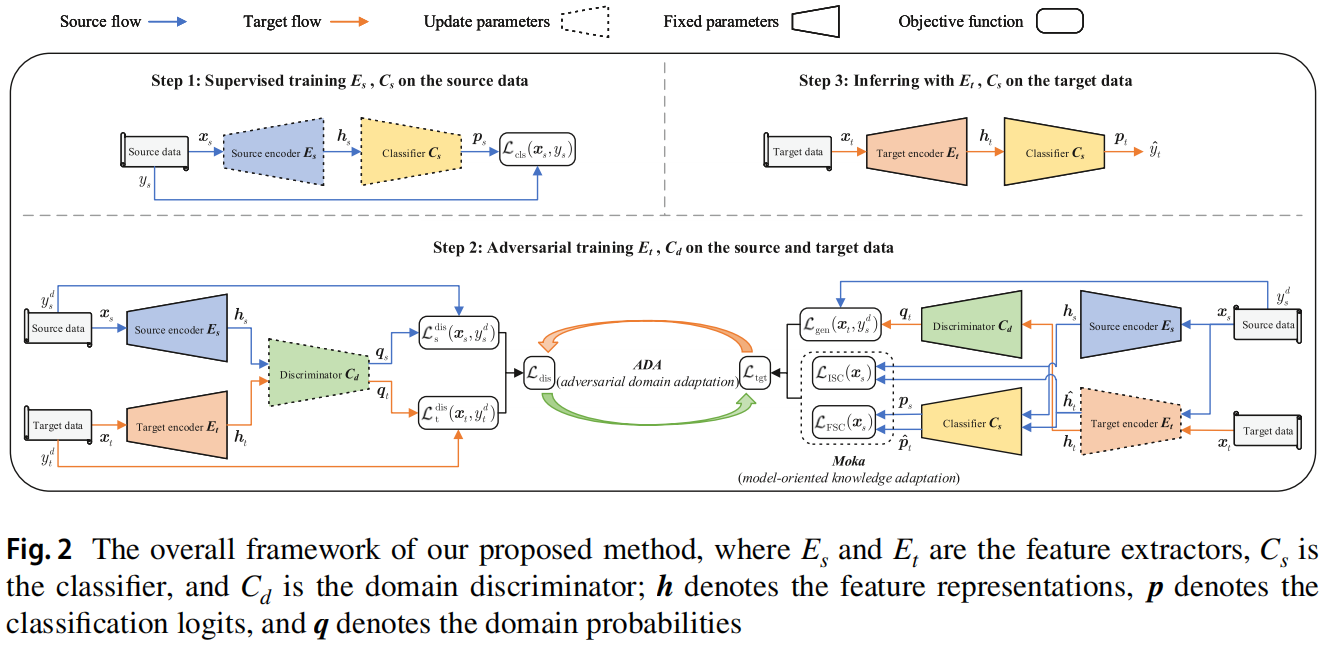
主要包括三个步骤:
- Step1:对源数据上的源编码器 $E_s$ 和分类器 $C_s$ 进行监督训练;
- Step2:对抗性训练目标编码器 $E_t$ 和鉴别器 $C_d$,以对齐源域和目标域分布;
- Step3:利用训练后的目标编码器 $E_t$ 和分类器 $C_s$ 对目标数据进行推断;
Step1,目标是使用来自源域的标记数据来训练一个性能良好的源模型,它作为目标模型的后续训练的 “teacher”,通过使用交叉熵损失,通过对源编码器 $E_s$ 和分类器 $C_s$ 在 $(x_s,y_s)$ 进行监督训练,可以最小化源误差:
$\begin{array}{l}\underset{E_{s}, C_{s}}{\text{min}} \; \mathcal{L}_{\mathrm{cls}}\left(\boldsymbol{x}_{s}, y_{s}\right)=\mathbb{E}_{\left(\boldsymbol{x}_{s}, y_{s}\right) \sim \mathbb{D}_{S}}-\sum_{k=1}^{K} \mathbb{1}_{\left[k=y_{s}\right]} \log \sigma\left(\boldsymbol{p}_{s}\right)\end{array}$
Step2,固定 $E_s$ 的参数,并使用 $E_s$ 初始化 $E_t$ 的参数,接着进行对抗性训练:
域分类损失最小化:
$\begin{aligned}\underset{C_{d}}{\text{min}} \; & \mathcal{L}_{\mathrm{dis}}\left(\boldsymbol{x}_{s}, \boldsymbol{x}_{t}, y_{s}^{d}, y_{t}^{d}\right) \\& =\min _{C_{d}}\left[\frac{\mathcal{L}_{\mathrm{s}}^{\mathrm{dis}}\left(\boldsymbol{x}_{s}, y_{s}^{d}\right)+\mathcal{L}_{\mathrm{t}}^{\mathrm{dis}}\left(\boldsymbol{x}_{t}, y_{t}^{d}\right)}{2}\right] \\& =\frac{\mathbb{E}_{\boldsymbol{x}_{s} \sim \mathbb{D}_{S}}-\log \left(1-\boldsymbol{q}_{s}\right)+\mathbb{E}_{\boldsymbol{x}_{t} \sim \mathbb{D}_{T}}-\log \boldsymbol{q}_{t}}{2} .\end{aligned}$
域分类损失最大化(迷惑域鉴别器):
$\begin{aligned}\underset{E_{t}}{\text{min}} \;\; & \mathcal{L}_{\text {gen }}\left(\boldsymbol{x}_{t}, {\color{Red} y_{s}^{d}} \right) \\\quad & =\mathbb{E}_{\boldsymbol{x}_{t} \sim \mathbb{D}_{T}}-\left[y_{s}^{d} \log \boldsymbol{q}_{t}+\left(1-y_{s}^{d}\right) \log \left(1-\boldsymbol{q}_{t}\right)\right] \\& =\mathbb{E}_{\boldsymbol{x}_{t} \sim \mathbb{D}_{T}}-\log \left(1-\boldsymbol{q}_{t}\right),\end{aligned}$
注意:对抗性训练中的 特征提取器这边指的是 目标编码器 $E_t$;
目标编码器的最终训练目标:
$\begin{array}{l}\underset{E_{t}}{\text{min}}\;\mathcal{L}_{\mathrm{tgt}}\left(\boldsymbol{x}_{s}, \boldsymbol{x}_{t}, y_{s}^{d}\right) \\\quad= \underset{E_{t}}{\text{min}}\left[\mathcal{L}_{\mathrm{gen}}\left(\boldsymbol{x}_{t}, y_{s}^{d}\right)+\mathcal{L}_{\mathrm{ISC}}\left(\boldsymbol{x}_{s}\right)+\mathcal{L}_{\mathrm{FSC}}\left(\boldsymbol{x}_{s}\right)\right]\end{array}$
Step3,使用训练好的目标编码器 $E_t$ 和分类器 $C_s$ 对用于测试的目标数据情绪极性标签预测如下:
$\hat{y}_{t}=\arg \max \boldsymbol{p}_{t}$
2.3 算法流程
长这样的算法步骤:

3 实验
数据集

情绪分类结果

可视化
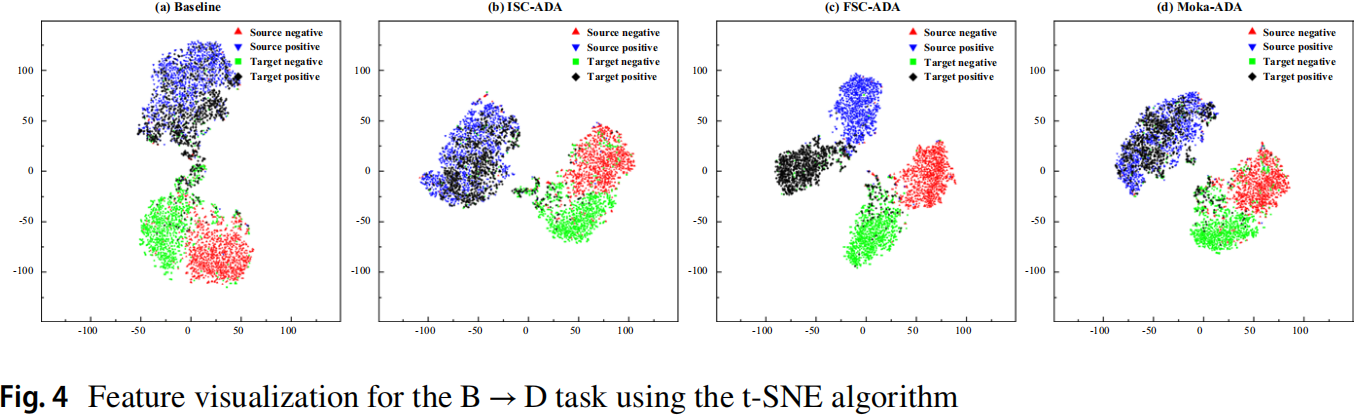
消融实验
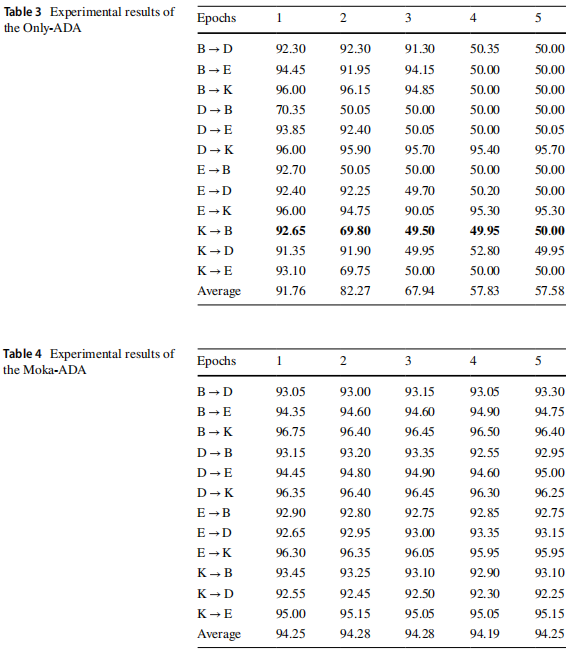
论文解读(Moka‑ADA)《Moka‑ADA: adversarial domain adaptation with model‑oriented knowledge adaptation for cross‑domain sentiment analysis》的更多相关文章
- 论文解读( FGSM)《Adversarial training methods for semi-supervised text classification》
论文信息 论文标题:Adversarial training methods for semi-supervised text classification论文作者:Taekyung Kim论文来源: ...
- 论文解读(JKnet)《Representation Learning on Graphs with Jumping Knowledge Networks》
论文信息 论文标题:Representation Learning on Graphs with Jumping Knowledge Networks论文作者:Keyulu Xu, Chengtao ...
- 论文解读(CDCL)《Cross-domain Contrastive Learning for Unsupervised Domain Adaptation》
论文信息 论文标题:Cross-domain Contrastive Learning for Unsupervised Domain Adaptation论文作者:Rui Wang, Zuxuan ...
- 论文解读(CAN)《Contrastive Adaptation Network for Unsupervised Domain Adaptation》
论文信息 论文标题:Contrastive Adaptation Network for Unsupervised Domain Adaptation论文作者:Guoliang Kang, Lu Ji ...
- CVPR2020论文解读:三维语义分割3D Semantic Segmentation
CVPR2020论文解读:三维语义分割3D Semantic Segmentation xMUDA: Cross-Modal Unsupervised Domain Adaptation for 3 ...
- 图像分类:CVPR2020论文解读
图像分类:CVPR2020论文解读 Towards Robust Image Classification Using Sequential Attention Models 论文链接:https:// ...
- 论文解读(SR-GNN)《Shift-Robust GNNs: Overcoming the Limitations of Localized Graph Training Data》
论文信息 论文标题:Shift-Robust GNNs: Overcoming the Limitations of Localized Graph Training Data论文作者:Qi Zhu, ...
- itemKNN发展史----推荐系统的三篇重要的论文解读
itemKNN发展史----推荐系统的三篇重要的论文解读 本文用到的符号标识 1.Item-based CF 基本过程: 计算相似度矩阵 Cosine相似度 皮尔逊相似系数 参数聚合进行推荐 根据用户 ...
- CVPR2019 | Mask Scoring R-CNN 论文解读
Mask Scoring R-CNN CVPR2019 | Mask Scoring R-CNN 论文解读 作者 | 文永亮 研究方向 | 目标检测.GAN 推荐理由: 本文解读的是一篇发表于CVPR ...
- AAAI2019 | 基于区域分解集成的目标检测 论文解读
Object Detection based on Region Decomposition and Assembly AAAI2019 | 基于区域分解集成的目标检测 论文解读 作者 | 文永亮 学 ...
随机推荐
- 如何利用Requestly提升前端开发与测试的效率,让你事半功倍?
痛点 前端测试 在进行前端页面开发或者测试的时候,我们会遇到这一类场景: 在开发阶段,前端想通过调用真实的接口返回响应 在开发或者生产阶段需要验证前端页面的一些 异常场景 或者 临界值 时 在测试阶段 ...
- 基于CentOS 7.6安装及配置APISIX 3.0环境
最近一直在研究微服务相关内容,通过对比各大API网关,发现新起之秀 APISIX无论从开源程度上来讲还是功能上,都拥有很大的优势. 经历了几天折磨一样的学习,目前在本地环境中配置成功了一套,以供自己留 ...
- #Powerbi 理解VAR函数
VAR意思即为变量,在编程语言中,变量是一个重要概念,DAX作为一种语言也有变量概念,利用VAR,我们可以缩短我们一些DAX语句的长度,更清晰的表达我们的度量值计算逻辑. 举例说明: 我们要计算一个产 ...
- 2021-04-09:rand指针是单链表节点结构中新增的指针,rand可能指向链表中的任意一个节点,也可能指向null。给定一个由Node节点类型组成的无环单链表的头节点 head,请实现一个函数完成这个链表的复制,并返回复制的新链表的头节点。 【要求】时间复杂度O(N),额外空间复杂度O(1) 。
2021-04-09:rand指针是单链表节点结构中新增的指针,rand可能指向链表中的任意一个节点,也可能指向null.给定一个由Node节点类型组成的无环单链表的头节点 head,请实现一个函数完 ...
- 2021-12-09:二叉树展开为链表。 给你二叉树的根结点 root ,请你将它展开为一个单链表: 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左
2021-12-09:二叉树展开为链表. 给你二叉树的根结点 root ,请你将它展开为一个单链表: 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左 ...
- vue中嵌入MP4 只有声音没图像
最近一个项目需要在页面嵌入一段视频,当然首选iframe了,直接嵌入了youku的视频,没问题,我想ok了.于是将url替换为本地的MP4发现只有声音没有任何图片,奇怪了,我首先想到是不是vue项目使 ...
- cv学习总结(10.31-11.6)
这一周主要焦点在于实现反向传播和全连接两层神经网络的具体代码以及书写博客记录课程学习的心得体会,目前完成了反向传播的具体代码以及相应博客的书写,完成了assignment1中figure的SVM版提取 ...
- ODOO升级可能遇到问题
a,找不到模块或视图不存在. 解决方案:查看是否将相应py文件加入到__init__文件中,或xml文件加入到manifest->data文件中. b, 找不到关联模块. 解决方案:这种一般要么 ...
- odoo开发教程四:onchange、唯一性约束
一:onchange机制[onchange=前端js函数!可以实现前端实时更新以及修改验证] onchange机制:不需要保存数据到数据库就可以实时更新用户界面上的显示. @api.onchange( ...
- Simple CTF
来自tryhackme的Simple CTF IP:10.10.27.234 信息收集 端口扫描 nmap -sV -T4 10.10.27.234 可以看到三个端口 21/tcp 打开 ftp vs ...
