加密解决HTTP协议带来的安全问题

HTTP协议默认是采取明文传输的，容易被中间人窃听、拦截、篡改，存在安全隐患。

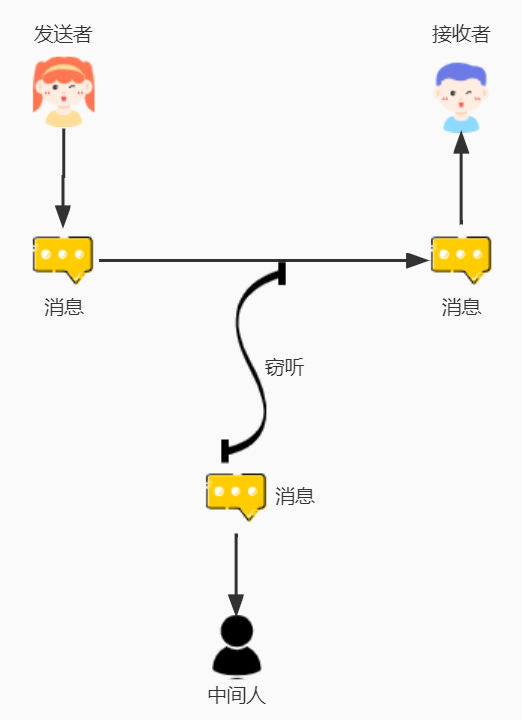
常见提高安全性的方法是对通信内容进行加密，再进行传输，常见的加密方式有

不可逆加密：单向散列函数

可逆加密：对称加密、非对称加密

其它组合加密：混合密码、数字签名、证书

单向散列函数

单向散列函数是一种不可逆的加密方式，加密后不能再解密将数据恢复原样，通过单向散列函数根据根据消息内容计算出散列值，无论消息的长度、大小是多少，最终生成的散列值长度都是固定值。

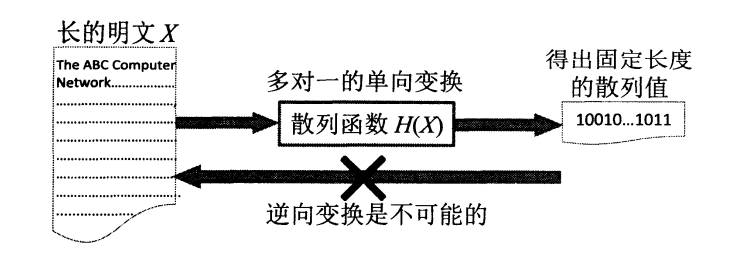
常见的散列函数有 MD5、SHA，虽然说具备单向性，但仍然有些网站可以暴力破解较为简单的内容。

但加密的原始内容更为复杂的话，破解的可能性就会较为小一些，比如开启大小写+字符的方式。

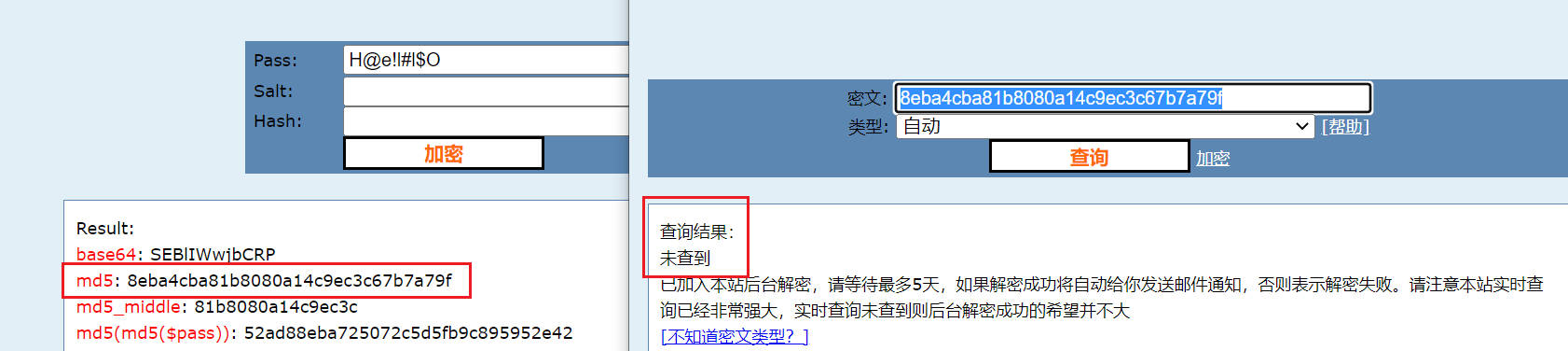
不可逆的加密方式可用于保存一些不需要还原的敏感信息，比如用户的密码，如果明文存放无论是开发者、网络维护人员看到、或者被黑客攻击都会存在信息泄露的问题，那么加密保存便是一种比较合适的方式。

比如当用户注册时，保存的密码是经过单向散列函数加密存放在数据库的，当用户登录时，将输入的密码加密后和数据库中保存的进行比较。即使用户忘记密码，也无需考虑还原原密码，让用户重新设置新密码即可。

对称加密

在对称加密中，加密、解密时使用的是同一个密钥。

对称加密算法常用 DES、3DES、AES

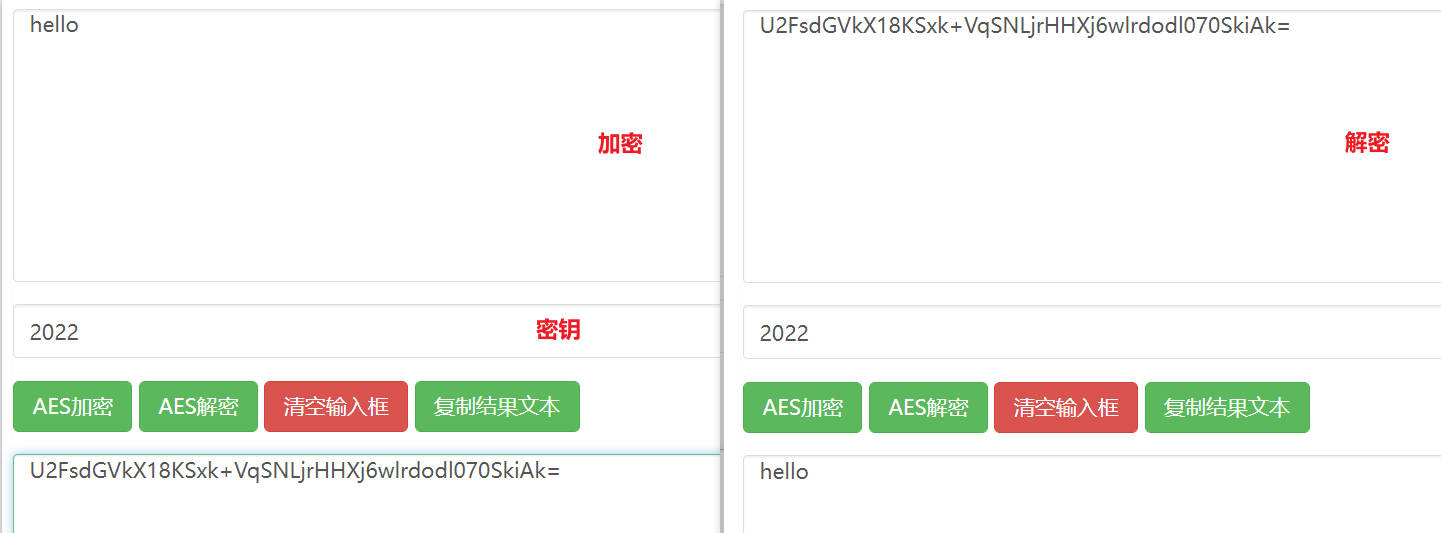
对称加密密钥如何配送仍然会存在问题，除非私下共享，只要经过网络明文传输，都存在被拦截窃取的可能。

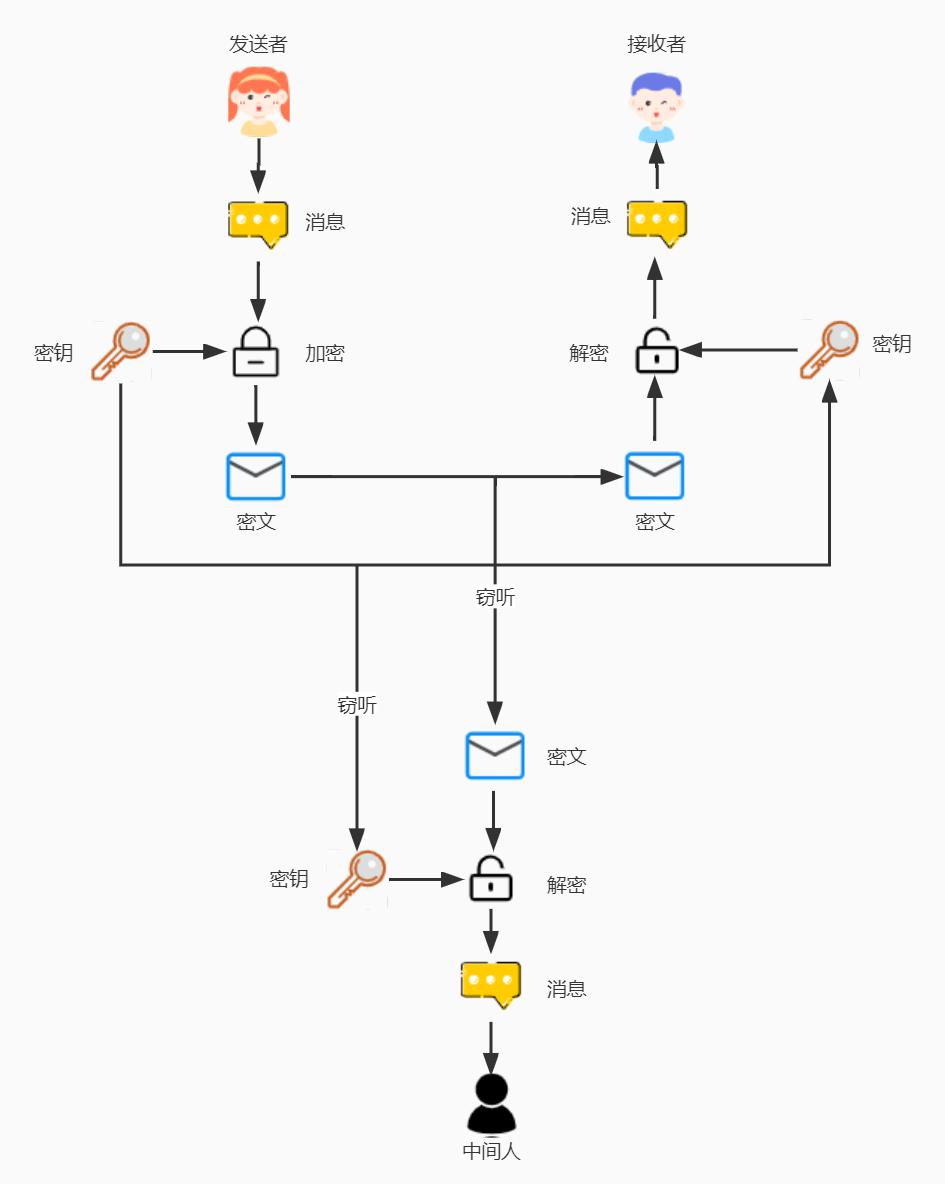
我们换个思路，是否存在一种加密方式，即使配送密钥的被窃取了，也不用担心，因为单单只用一个密钥不会影响数据传递。非对称加密就是这样，加密和解密都需要公钥和私钥两个密钥共同协作。

非对称加密

在非对称加密中，密钥分为加密密钥和解密密钥，两者并不相同，加密密钥一般是公开的，因此也称为公钥，解密密钥由消息接收者自己保管，不能公开，也称为私钥。

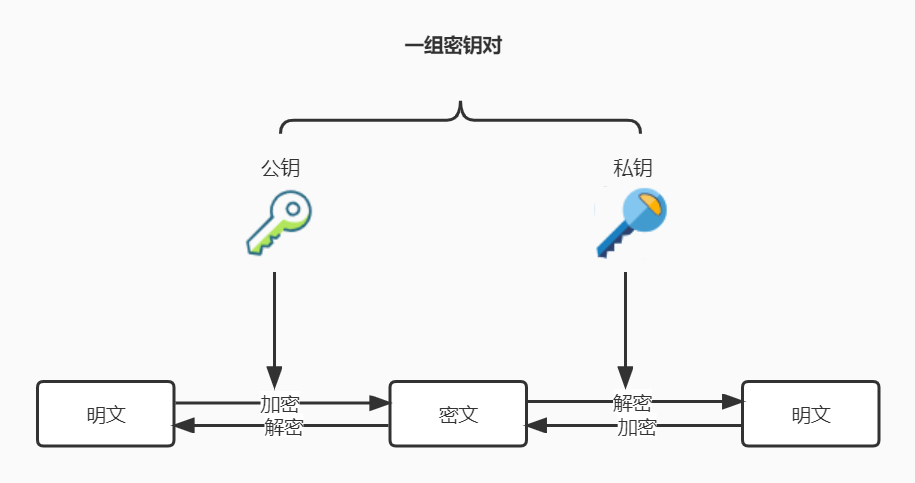
公钥和私钥是一一对应的，不能单独生成，一堆公钥和私钥统称为密钥对，由公钥加密的密文，必须使用与该公钥对应的私钥才能解密，由私钥加密的密文，必须使用与该私钥对应的公钥才能解密。

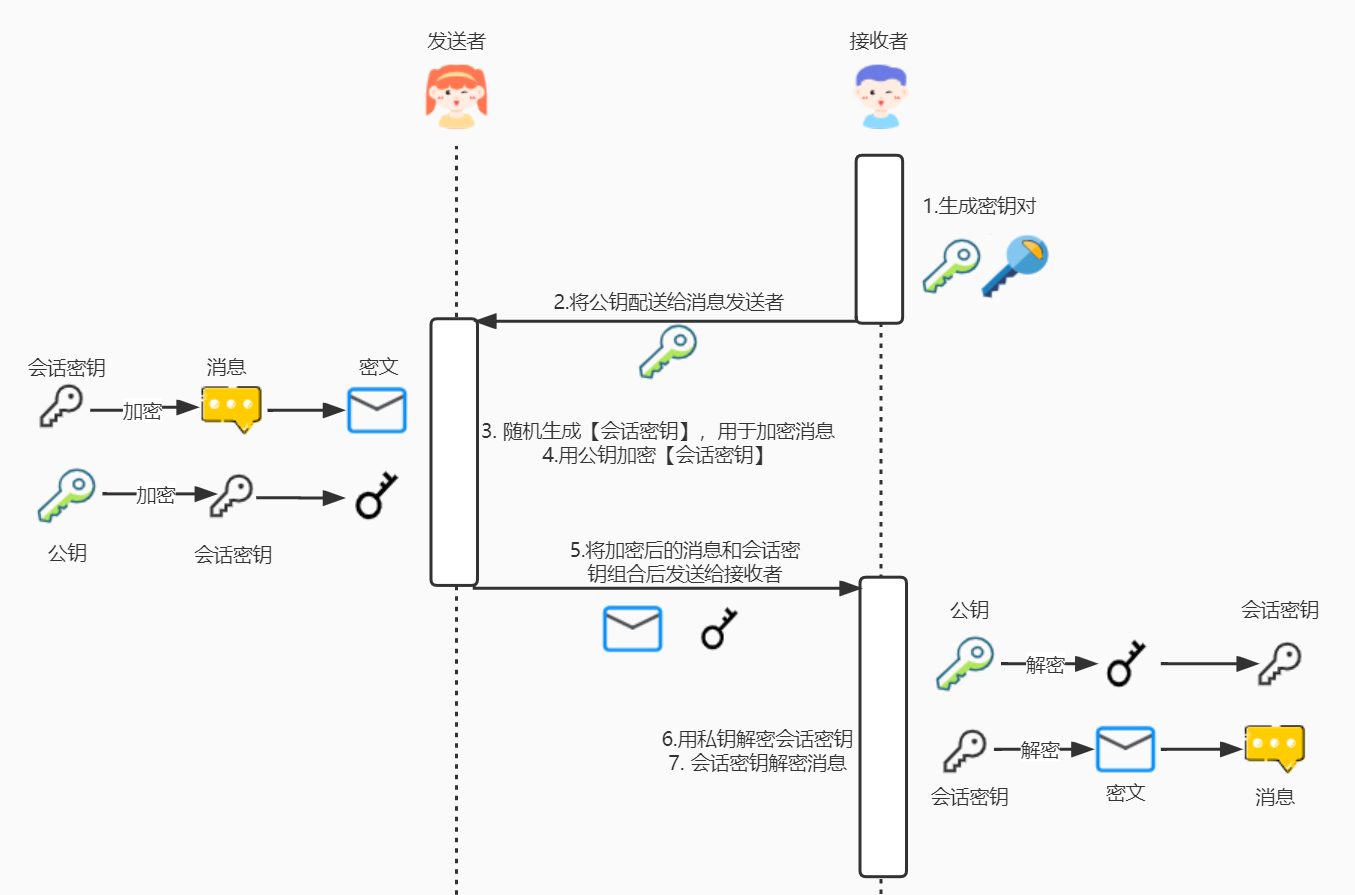
这样，使用非对称加密便可以解决密钥配送问题，由接收者生成密钥对，将公钥配送给消息发送者，发送者通过公钥加密消息后，发送密文给接收者，接收者再通过私钥解密消息。

在这个过程中，即使消息、公钥被中间人窃听也没关系，因为公钥加密的消息只可通过对应的私钥解密，而私钥是保存在接收者处的。

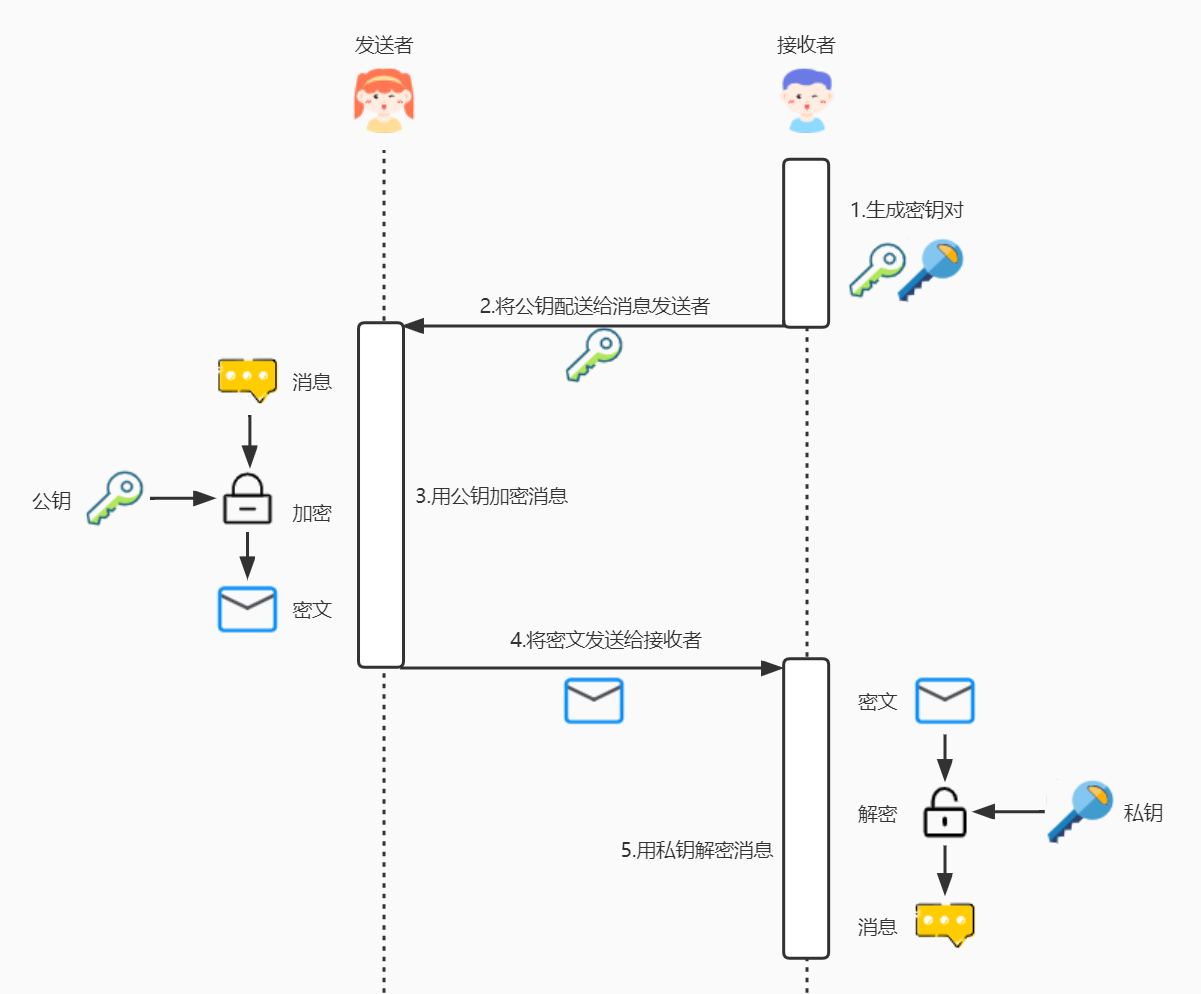
非对称加密比较安全，解决了密钥的配送问题，但它的加密速度比对称加密要更慢一些，如果所有内容都采用非对称加密，那网络上通信将变得非常慢。

混合密码

混合密码是将对称加密和非对称加密优势相结合的方法，解决了对称加密的密钥配送，非对称加密速度慢的问题。

使用对称加密将消息加密，再通过非对称加密算法加密对称加密的密钥，这样就能保证复杂的内容使用加密较快的对称加密，而重要的信息通过非对称加密。

数字签名

以上方式从接收者的角度，可以保证消息的在传输过程的安全，但如何能保证来源的可靠性呢？如果被窃听，中间人也是可以通过公钥加密伪造消息发送给接收者的。

数字签名 就是一种保障来源的方式，与以上混合加密不同，是由消息发送者的私钥生成签名，由消息接收者通过公钥验证签名。

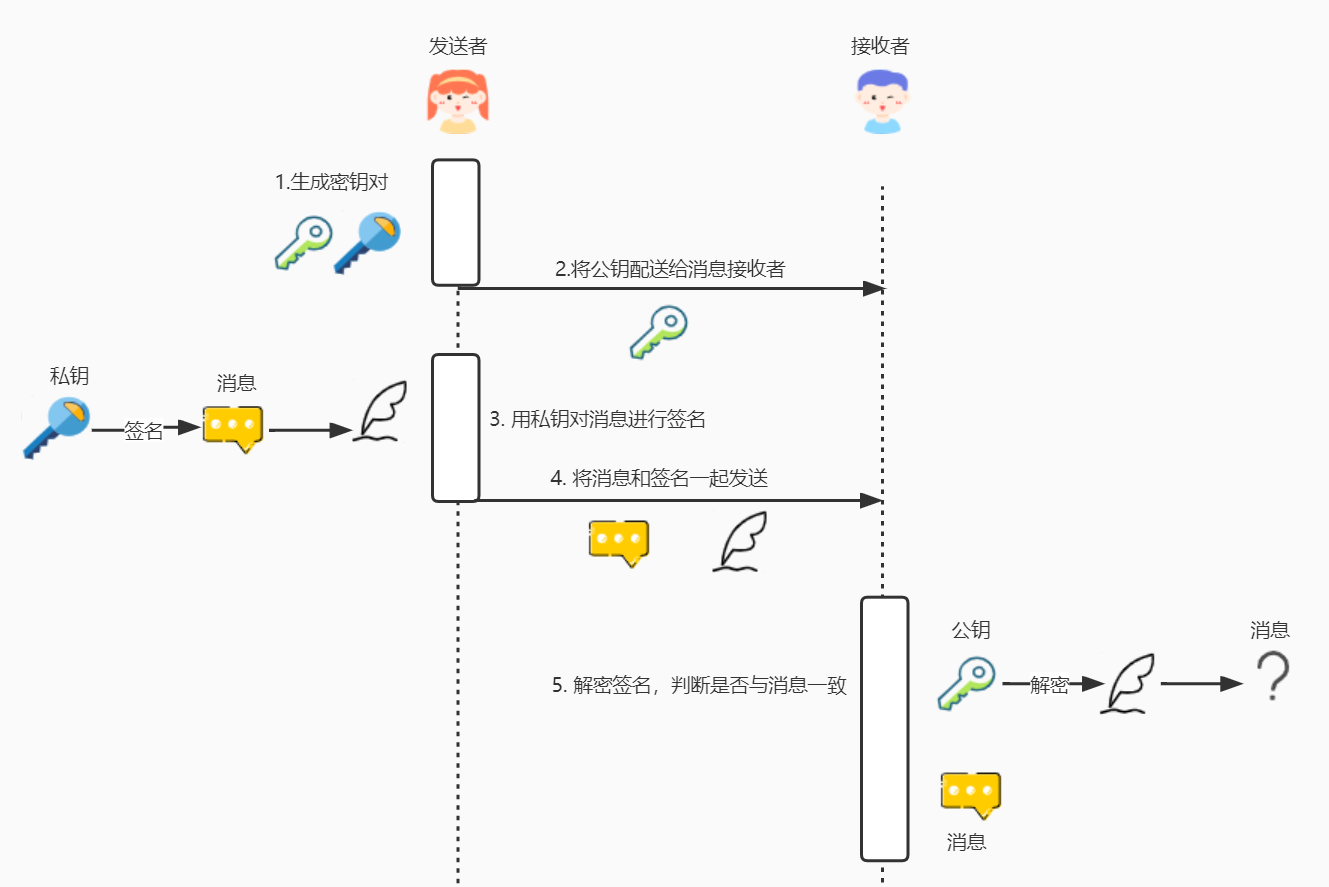
消息是明文传输不安全，并且使用非对称加密所有的消息会比较耗时，可以改进为使用散列函数将消息加密，再通过私钥对散列函数加密，因为散列函数不可逆可以解决安全问题，并且散列函数处理过的数据长度是一个比较短的固定值，能解决耗时的问题。

证书

公钥的配送仍然可能存在问题，如果存在中间人窃听了公钥，可以自己生成一套密钥对，并将自己的公钥传递给消息发送方。

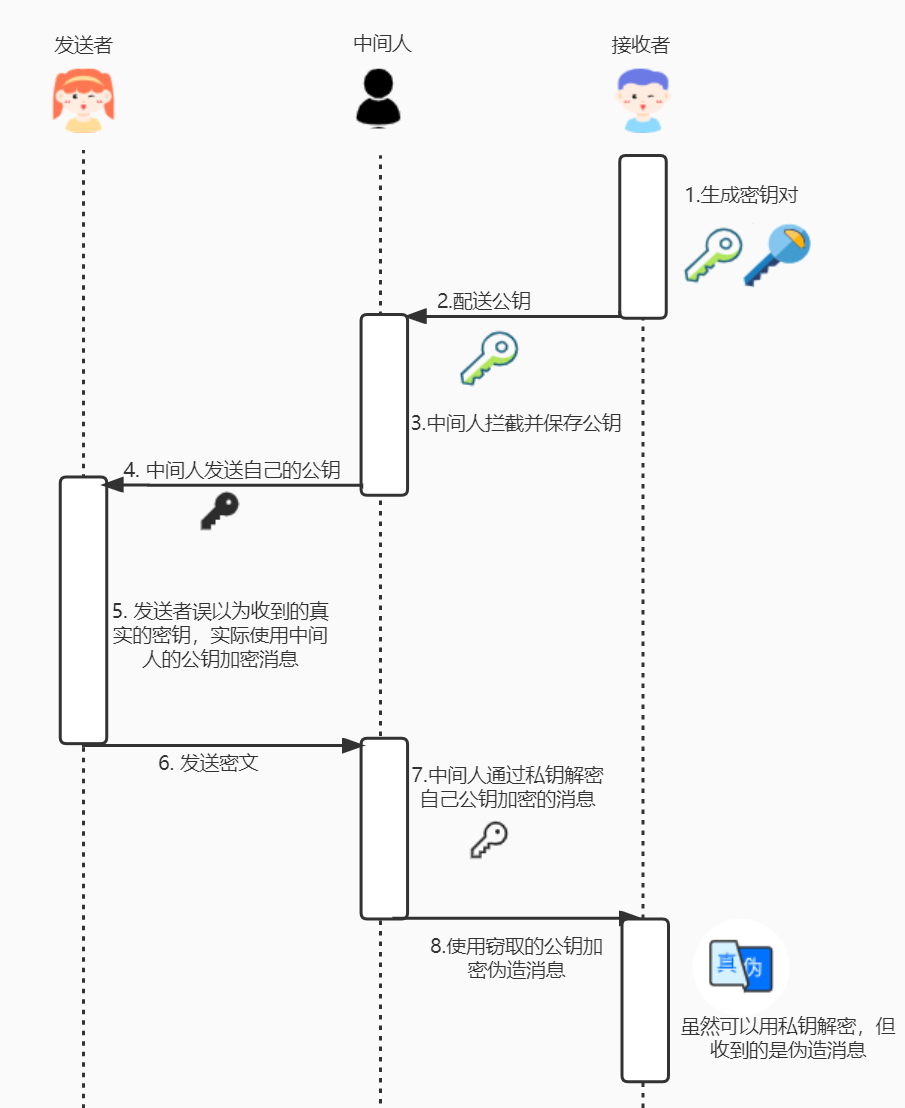
为了保证公钥的安全性，可以依靠于认证机构来颁发数字签名。

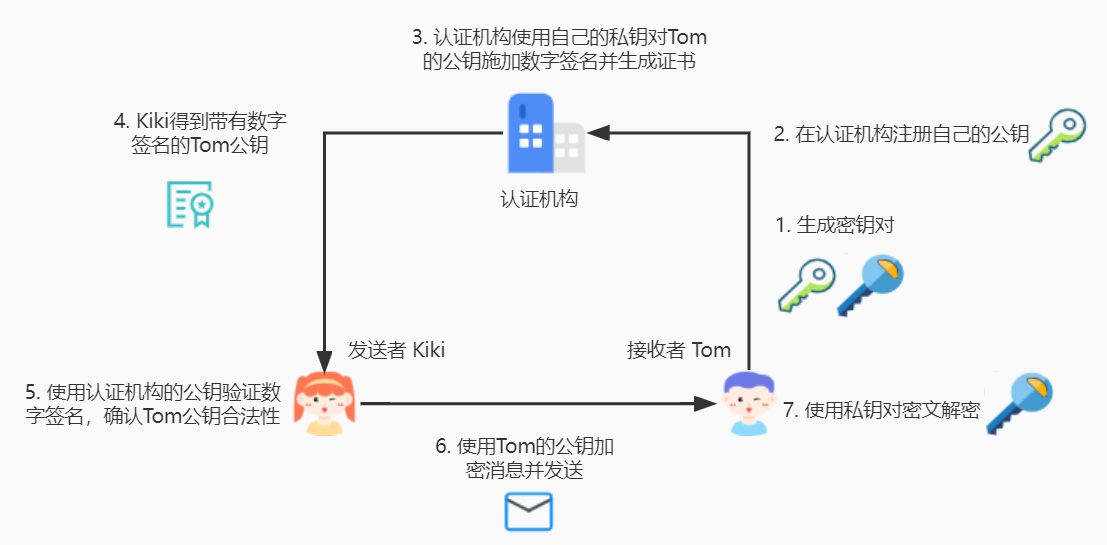
总结

单向散列函数不可逆，加密后长度固定
对称加密解密使用的是相同的密钥，加密速度较快，但密钥的配送存在安全问题
非对称加密存在密钥对，分为加密密钥公钥和解密密钥私钥，加密速度较慢
混合密码结合对称加密和非对称加密，同时做到安全和较快的加密速度
数字签名用于确认消息的完整性，识别消息是否被篡改
证书保证公钥的安全

以上就是各种加密方式，以解决HTTP协议带来的安全问题。更多有关 前端、网络协议 的内容可以参考我其它的博文，持续更新中~