解析数仓lazyagg查询重写优化

摘要：本文对Lazy Agg查询重写优化和GaussDB(DWS)提供的Lazy Agg重写规则进行介绍。

本文分享自华为云社区《GaussDB(DWS) lazyagg查询重写优化解析【这次高斯不是数学家】》，作者： OreoreO 。

聚集操作将查询结果按某一列或多列的值分组，值相等的为一组。聚集操作是一种常见的操作并在金融客户中有广泛的使用。例如如下语句：

SELECT a, count(a) FROM t1 GROUP BY a; -- 按a分组并计算分组内重复值的个数

一、Lazy Agg重写规则

数据量大的场景下，聚集运算由于数据量大导致下盘，聚集操作执行时间成为性能瓶颈，从而导致整个查询执行效率非常差。例如：

SELECT t2.b, sum(cc) FROM (SELECT b, sum(c) AS cc FROM t1 GROUP BY b) AS s, t2 WHERE s.b=t2.b GROUP BY t2.b;

子查询对t1.b列进行聚集，对t1.c列求和，在外部查询中，同样也存在聚集运算，对子查询的聚集求和列cc列求和。对于这类语句，当子查询的聚集运算较耗时的情况下，可以利用查询重写规则消除子查询的聚集运算，由外部查询的聚集函数统一完成聚集运算。消除子查询后可能导致子查询行数增多，但对于子查询聚集运算时t1.b列的distinct值较多的场景，子查询聚集运算后的行数较原表不会有明显缩减，不会导致外层JOIN运算量的大量增加。即语句可被重写为：

SELECT t2.b, sum(cc) FROM (SELECT b, c AS cc FROM t1) AS s, t2 WHERE s.b=t2.b GROUP BY t2.b;

这个改写规则称为Lazy Agg，适用于基表数据量大且distinct值较多的场景。如果重复值较少，那么消除了聚集操作会导致Join后的行数激增，Join性能较差，因此需要将Agg下推到Join之前进行，通过提前的Agg操作减少Join结果的行数，这个改写规则称为Eager Agg。

二、GaussDB(DWS) lazyagg优化

为了降低调优难度，提升产品易用性，GaussDB(DWS)提供了lazyagg查询重写优化规则，可以通过设置guc参数rewrite_rule包含’lazyagg’使用Lazy Agg查询重写优化。开启lazyagg查询重写优化后，对满足条件的场景会优化并消除子查询中的聚集操作。原计划如下所示：

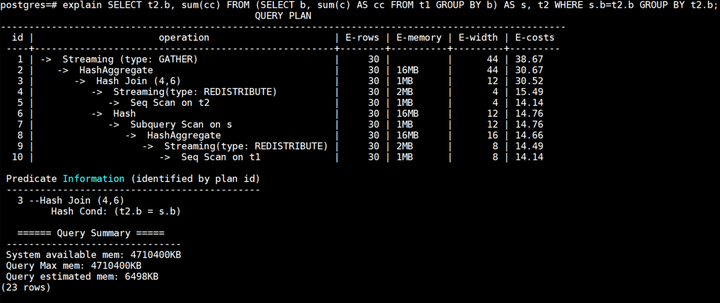
lazyagg重写优化后计划如下所示：

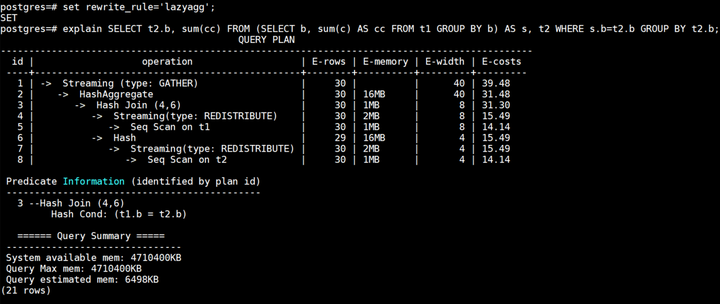
可以看到相比于原计划，lazyagg重写优化后消除掉了原计划中的聚集操作，即7号Subquery Scan算子和8号HashAggregate算子。

三、lazyagg优化规格

支持子查询为单一聚集查询或包含聚集子集合操作的查询。集合操作仅支持UNION ALL，可对部分分支子查询进行聚集运算消除。子查询需为JOIN表之一（不在TargetList、Where子句等其他位置）。
支持若外部查询的所有Agg参数列包含于其某个子查询的Agg函数列，则可对该子查询的聚集运算进行消除。
支持所有消除子查询聚集运算后结果正确的聚集函数种类。聚集函数种类结果正确性见下表：

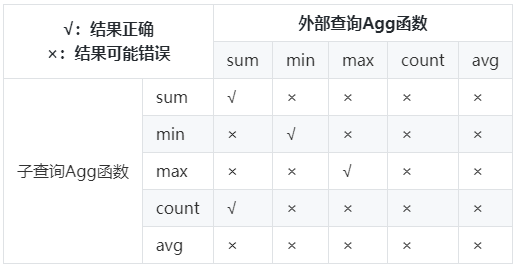
4. 场景约束
在上述场景扩展的基础上，对于可能导致结果错误的场景，不进行查询重写，包括但不限于：

不支持消除的Agg函数类型。
子查询中包含其它条件或算子，会导致重写后结果错误，例如HAVING、window agg、LIMIT、OFFSET、AP function、distinct、recursive等。
外层Agg参数列、GROUP BY列或JOIN列中包含volatile函数，如random、timeofday等。
子查询Agg函数外、外部查询Agg函数内有其他表达式或函数操作，如子查询Agg函数列为sum+1、max+max(d)，外部查询Agg函数列为sum(cc+1)等。
外部查询的JOIN列、GROUP BY列或其它条件中包含子查询Agg函数列。
子查询在LEFT JOIN、RIGHT JOIN的inner边或FULL JOIN中，且子查询Agg函数为count，外部查询Agg函数为sum的。

四、结语

通过本文的分析，相信用户朋友已经充分了解了Lazy Agg重写优化的使用场景，以及GaussDB(DWS)的lazyagg实现方式。希望广大用户能够通过深入的了解，对GaussDB(DWS)的性能调优产生浓厚的兴趣并深度参与进来。

参考文档：
GaussDB(DWS)性能调优系列实战篇四：十八般武艺之SQL改写

理论不如实践，那如何快速体验DWS呢？DWS现推出了一项Demo体验活动。进入DWS首页，点击“Demo体验”，快速便捷体验一把！（体验过程中有任何建议和意见，可以去DWS社区论坛反馈哦）

点击关注，第一时间了解华为云新鲜技术~