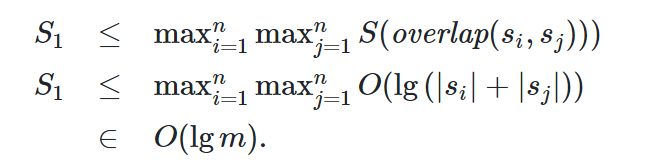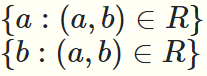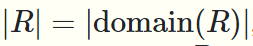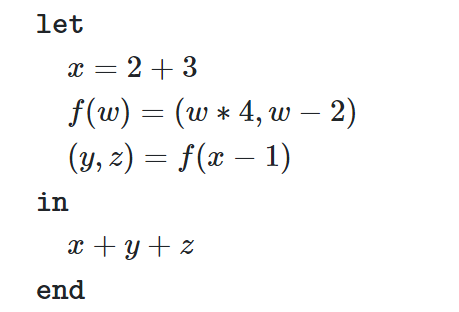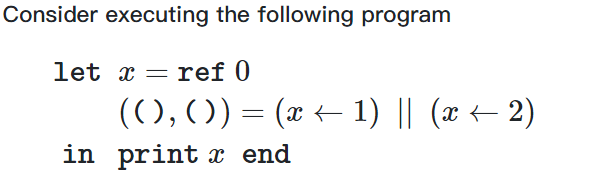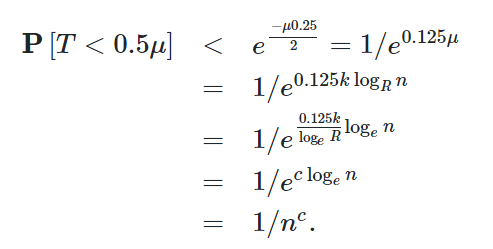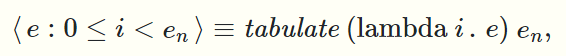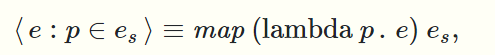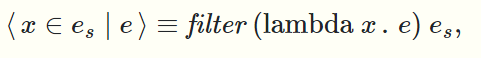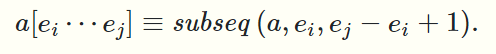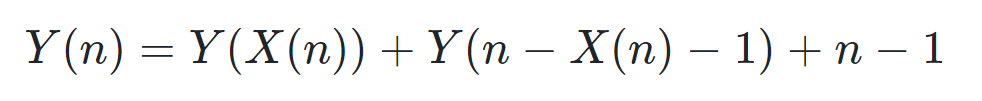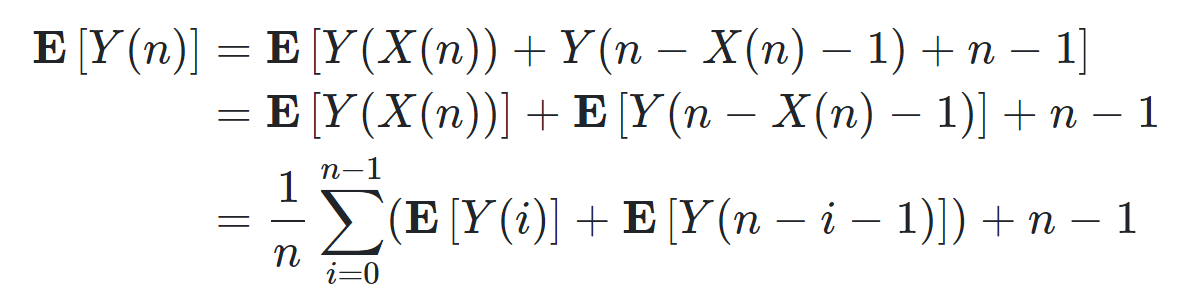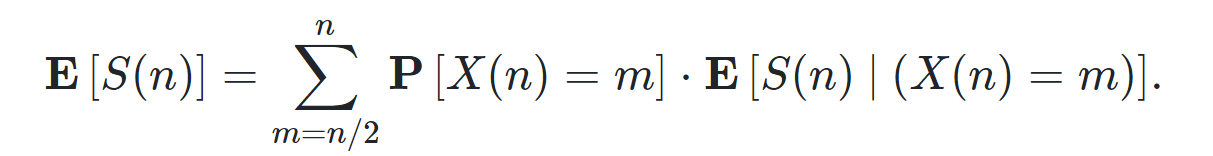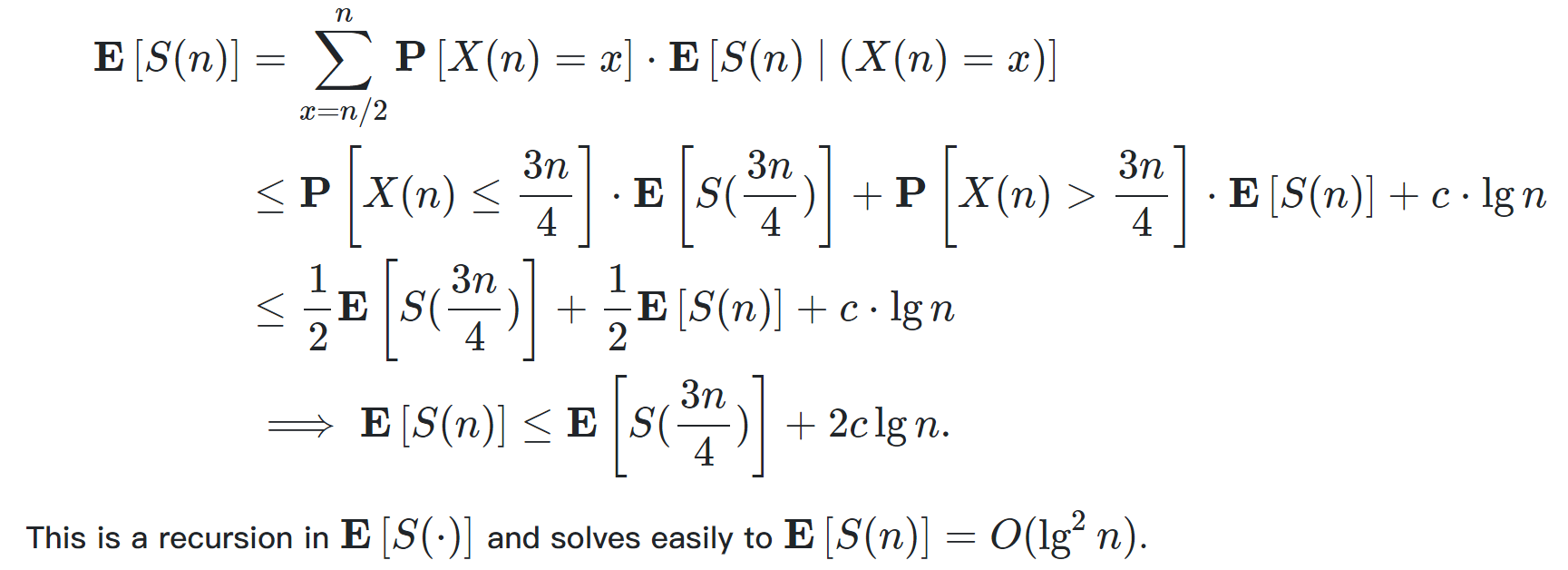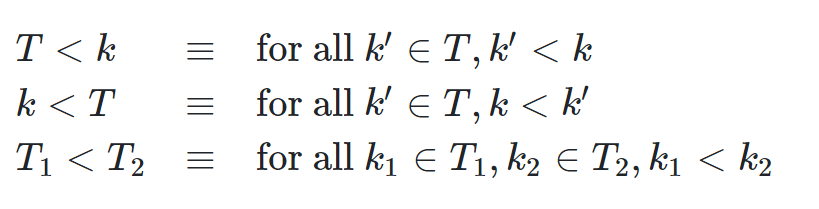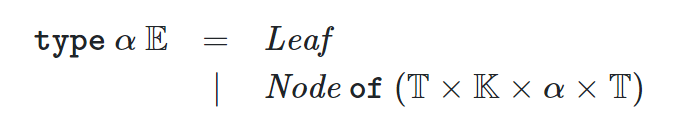Parallel and Sequential Data Structures and Algorithms

并串行

从零开始考前突击并串行数据结构与算法

强烈建议和原教材参照着看

Introduction

本书的要点

1. 定义问题
2. 不同的算法解决
3. 设计抽象数据类型和相应的数据结构实现
4. 分析比较算法和数据类型的代价

并行的原因：

1. 时间宝贵
2. 加快计算速度意味着能量消耗立方级的增加

并行的speed up范围

并行算法要求计算之间没有依赖关系，如何削减不必要依赖是设计重点

Work是操作的总数 Span是最长的计算依赖序列

总时间代价为\(\frac{W}{P}\)，是最理想的speed up

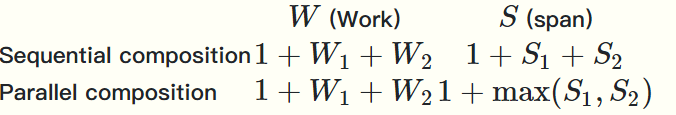
当W \(\gg\) S时我们可以期待这个问题的并行算法有很好的speed up

当评价并行算法时，Work是首要衡量因素，其次才是Span，当Work和串行下的最优算法在同一量级时称之为work efficiency

问题分为算法问题和数据结构问题，区别在于后者要解决一系列算法问题（对应着每个操作）

如何定义问题：

1. 定义算法 (通过指定算法要做的事)和算法的代价(通过指定work和span)
2. 定义抽象数据类型及其操作（通过指定ADT的意义和操作会做什么事）以及操作的代价(通过给出work和span)

我们使用伪代码来描述算法，这样可以将问题分解为多个函数模块

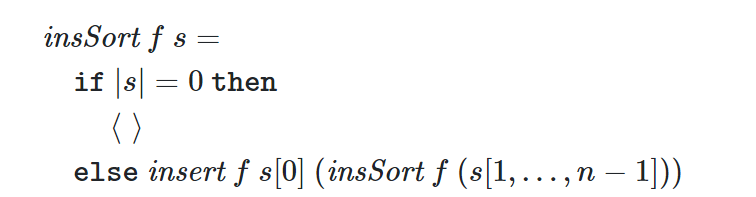
例如图中的描述insSort的伪代码中用到了insert

我们可以指定insert的work和span来分析insSort的work和span是否符合设计目标，如果符合接下来问题就缩小为设计insert

数据类型问题则可以通过指定一种实现的数据结构，进而转化为一系列的算法问题

这种分析方式使得我们

1. 可以忽略设计细节
2. 可以实现模块化问题分析
3. 有利于分析问题的不同

基因测序问题：将同一段基因序列复制多份，打碎得到许多碎片，求解原本的基因序列

子序列，前缀，后继的定义

克莱尼闭包的定义 Kleene plus 不包含空串 Kleene star包含空串

最短超串问题 找到一个最短的字符串，使得给定的所有串都是它的子串，其中所有串都由\(\sum\)中的元素组成

我们将基因测序问题转换为 SS问题，其中\(\sum\)为{a, c, g, t}

通过进一步观察问题得到一些规律

• 如果一个碎片A是另一个碎片B的子串，那么可以忽略A

定义不是其他碎片子串的碎片为片段

• 片段的开头在基因序列中位置不可能相同（否则一定有一个片段是另一个片段的子串，违反片段的定义），换句话说片段的开头在基因序列中的位置是一个严格的可排序列

这样片段的开头的排列就对应着可能的基因序列，我们要找出最短的那个，也就是找出一种排列使片段之间能够尽可能地出现重叠

定义\(overlap(s_i,s_j)\)为重叠数

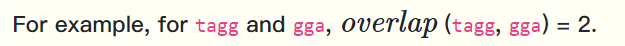
之后我们考虑暴力算法，计算n个碎片的\(n^2\)个overlap，找出一种排列使得overlap之和最多

代价分析：overlap比较字符串s和t的所有后继与前缀，Work为O(s*t),Span为O(lg(s+t)) PS:使用tree reduce的方法

(m为n个片段的总长度)

暴力算法计算所有的overlap的Work和Span为

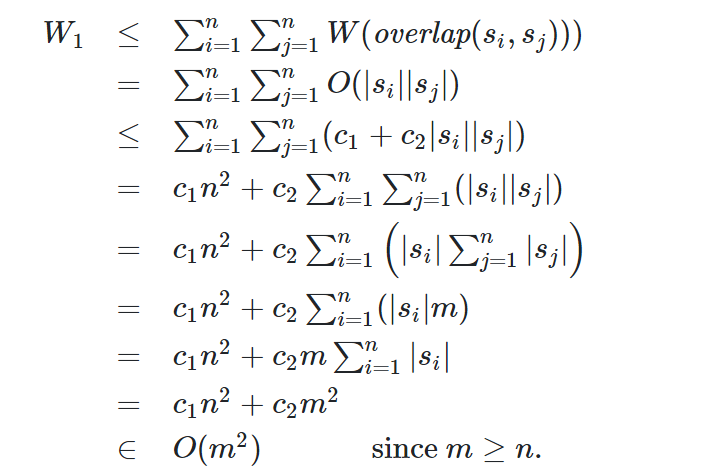
但找出一种排列使得overlap最大并不容易，因为我们有n！种排列

PS : 我们假设对每种排列的overlap求和Work为O(n),Span为O(lgn)

这里我们考虑将找到一种排列使overlap最大的问题转化为旅行商问题

其做法是如下

定义一个u节点，和n个节点表示片段

定义权重为

u节点到\(s_i\)节点的权重定义为\(s_i\)的长度，从\(s_i\)到u的权重为0 （\(s_i\)任意）

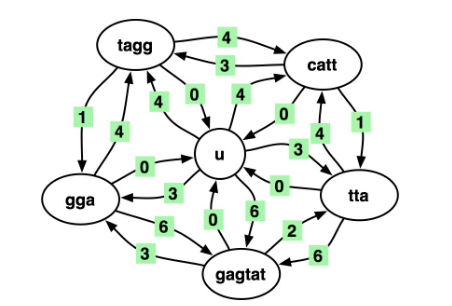
就像在这张图里，一个汉密尔顿回路对应一个排列，权重之和就对应着去掉overlap之后的长度

我们只要解决旅行商问题就能解决overlap和最大的问题了

当然两个问题都是NP——Hard问题，但NP-hard问题并不意味着不能快速计算近似解，对于这类问题我们甚至可以得到许多精确解决现实世界实例的算法

接下来我们要得到一个近似解，这就需要用到贪心算法

做法就是每次选取overlap最大的一对（贪心选择）（这一步用到reduce的方法并行计算），将其删去overlap的部分，视为一个节点，这样问题的规模就缩小1，直至问题规模为1，得到最终的序列

最终的算法是这样的：

1. 计算所有的overlap
2. 选择overlap最大的一对合并
3. 节点数减1，回到第一步

直到问题规模为1

因为计算overlap的步骤Work为O（\(m^2\)）,Span为O（\(lgm\)）,而第二部用reduce选择的Work为O(\(n^2\)),Span为O（\(lgn\)）,m>n,问题的时间代价由第一步决定

经过n次递归，总的Work为O（\(nm^2\)）,Span为O(nlgm),\(\frac{W}{S}\)很大，是一个高并行性的并行算法

这种近似算法的效果还是挺高的。 众所周知，它返回的字符串是最短字符串的 3.5 倍以内；据推测，该算法返回的字符串在 2 的因数内。实际上，贪心算法通常比推断的界限表现得更好。

真实的基因测序问题，要比刚刚解决的问题要更复杂，需要考虑更多因素

Background

集合的Partition是集合的一个分割，例如我们说P是集合A的一个分割，那么P也是一个集合，它的元素是A的非空子集合，且这些非空子集合彼此之间交集为\(\emptyset\),它们的∪恰好为A

回想一下克莱尼闭包的定义

A到B的一个关系是A，B的笛卡尔积的子集

假设我们有一个关系R，是A到B的关系

那么

第一个集合表示R的定义域

第二个集合表示R的值域

函数是定义域到至于的关系，且这个关系的元素的个数等于定义域的元素个数，也就是定义域中的一个元素只对应一个值

图的一些术语

这里的incident是“伴随的”的意思

路径的长度是路径中边的个数

顶点诱导子图是指包含了与 V' 中顶点相关联的所有边的子图

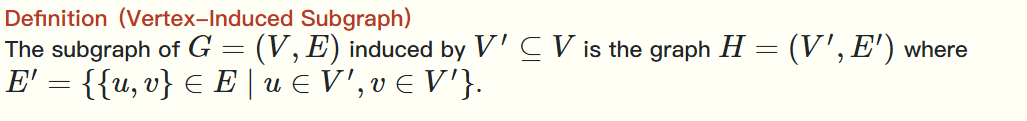
同理，边诱导子图是指包含了 E' 中边相关联的所有顶点的子图

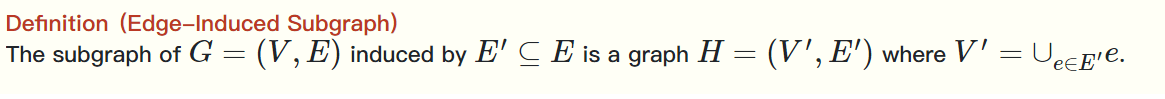
图的分割类似于集合的分割

首先将点集V进行分割，对应的\(E_1,E_2,\ldots\)为顶点诱导子图，这样就得到了图的分割

树的节点的深度是从根到这个节点的path的长度，高度是从这个节点到叶子节点的最长路径的长度

树高就是根的高度

Language

本书使用嵌套并行和函数式编程来描述并行算法和数据结构

嵌套并行是指：fork将开启一系列子任务（孩子），子任务计算完之后join，然后父亲继续进行

函数式编程是指：函数无side effect，从定义域映射到值域，可以用作值

SPARC 语言允许嵌套并行的写法，且只支持函数式编程（不允许有side effect）

SPARC 和其他函数式语言一样都是\(\lambda\) 表达式的扩展

side effect （副作用）在这里的定义是：除了根据输入返回一个输出外函数做的其他事（例如：写数据，打印一个值等等）

当函数没有side effect 称为pure function 当computation 用的function都是pure的，那么这个computation 是pure的

在pure computation 中没有数据可以被修改，只可能通过使用函数产生新的数据

当只使用pure computation时，并行一定是安全的，因为无论怎么操作并行之间都不会互相影响

否则，就可能出现computation之间相互影响（例如函数\(f\)修改了另一个函数\(g\)的结果），这时并行算法的结果就与timing有关了

当函数的一些中间变量被修改，但这种影响不会影响到函数外的任何内容，那么我们仍然可以认为这个函数是广义上的pure的，没有side effect

函数作为值的特性很神奇，（这里的函数是指一种对应关系，也就是说映射本身作为值）

例如

f(x)=

　let g(y)=x+y

　in g end

z=f(3)

这里z的值是一个给变量加3的函数，那么z(6)=9

再比如g(y)=y(6) 那么g(z)的含义就是z(6),因为函数作为值，那么z可以称为g(y)的实参，根据刚刚的定义g(z)=z(6)=9

g(f(5))中f(5)是一个给变量加5的函数，我们不妨将其记为函数k，那么g(f(5))=g(k)=k(6)=11

⟨f(3),f(1),f(6)⟩是一个序列包含三个函数，分别给参数加3，1，6

总结一下一个尚未传参的函数仍然可以当作一个值作为另一个函数的参数，组合出新的函数，且这些函数可以被保存在数据结构中，也可以当作被其他函数当作返回值返回

\(\lambda\)表达式有三种记号，一个计算原则

三种记号：

• x,y,z,… 表示变量
• λ x . e是一个\(\lambda\)式，x是变量，e是表达式 定义了一个函数，x是参数，e是函数体
• \(e_1 e_2\)是一个调用，\(e_1,e_2\)都是表达式，表示\(e_2\)要作为参数给到根据\(e_1\)得到的函数中进行计算

根据第三种形式，易知表达式是从右向左代入的，但在\(\lambda\)式中是将左侧的x代入到右侧的函数体中

同时，\(\lambda\)式也视作一个表达式

\(\lambda\)表达式本质上并行的，一个表达式的多个调用可以按任意次序进行计算，也就是说它可以并行

但按照一些计算次序可能可以递归到一个无法递归的形式（normal form），有些计算次序则不能

我们可能得到一个类似这样的结果，它可以无限递归

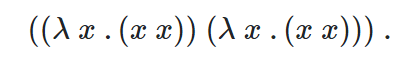
我们将右边的\(\lambda\)式当作参数代入到左边的\(\lambda\)式表示的函数中，也就是用右边的式子作为x代入函数体中，得到的仍是同样的\(\lambda\)表达式

常见的两种计算次序：

“call-by-value” 和 “call-by-need.”

call by value 是指只有当\(e_2\)被化简为一个值或者函数时，才将其代入到\(e_1\)中 ，本书使用call by value

call by need 则允许\(e_2\)也是一个调用，且我们对\(e_2\)不做化简，当\(e_1\)化简为一个函数时将\(e_2\)整个代入再化简新的\(e_1\)

call by value 中e1 e2同时化简，可以并行，call by need 不化简e2，先化简e1 然后代入 然后接着化简e1，是串行的

对SPARC语言的介绍包括：SPARC语言允许的语法，SPARC中的操作及其代价

SPARC语言的一个表达式就是一个程序，如果表达式里没有未定义的变量，那么最终的结果会是一个值，或者它会永远运行下去

SPARC允许的语法有：标识符 、模式 、类型 、数据类型 、值 、表达式 、操作 、绑定

标识符仅包含字母和数字字符（a-z、A-Z、0-9）、下划线字符（“_”），并且可以选择以一些“素数”结尾

在SPARC中我们用Type Constructors 给数据类型一个标识符 用Data Constructors复杂的数据结构一个标识符

模式是用来给出数据匹配的形式，例如一个数据对（x,y）或一个元组（x,y,z）

类型是SPARC包含的类型：整数 Z , 布尔型 B , 笛卡尔积形式 , 函数形式

数据类型是自定义的类型，是用data constructors组合一些类型（数据类型）得到的，数据类型支持递归定义

操作包含一些操作符

值是指不能进行递归的部分，包括：一些常量，一元原始操作，作用到值上的Data Constructors ，任意函数

SPARC中的表达式包括：中缀表达式\(e_1 op e_2\) 、顺序和并行组合（\(（e_1 ， e_2）\) 表示串行 \(（e_1 || e_2）\)表示并行，两者的返回值都是一个有序对）、条件表达式 、 条件句（if e1 then e2 else e3）、函数调用（与\(\lambda\)表达式相同）

条件表达式例如 将e1的值与Nil 和Cons（x,y）进行模式匹配，然后计算相应的e2或e3

绑定相当于对表达式e中的变量，函数，类型（数据类型）赋初值 ，常见的用法是let \(b^+\) in e

例如

依次执行绑定，最后代入到表达式e中

注意let 语句引导的绑定中，=右侧的表达式可以使用绑定中的任何函数和先于它绑定的变量的值 （这样能够支持相互之间的递归定义）

例如这个例子就用到了递归定义

Concurrency

线程的定义是：执行一段代码的计算

函数spawn：以一个表达式作为参数，开启一个线程，开始和其他线程并发地计算，返回值是线程

函数sync：以一个线程作为参数，等待它完成计算，这个函数没有返回值

这段代码开启两个线程，并行的计算Fibonacci数列并将结果保存到r ，s的地址，用sync函数确保计算完了，用！r , ! s 取出所指地址的值

PS：（） 表示空

并发是问题的属性，并行是问题解决方法的属性

非并发的问题也可能可以用并行算法解决

SPARC中我们可以将||符号替换为，来获得并行算法的串行版本，对于pure computation并行算法和其串行版本得到的结果是完全相同的

但当computation不是pure的

例如

可以看出，存在相同的引用和破坏性更新，也就是数据出现了mutable state(可变状态)，这个程序的结果无法不确定，且其计算结果和其串行版本的计算结果可能不同

这个程序的计算结果也无法确定，因为\(x\leftarrow x+1\)不是一个原子操作（包括读x，计算x+1，写入x）考虑在一个操作写入x之前另一个操作读了x，那么就相当于只加了一次

但我们在设计并行算法仍不可避免地产生mutable state，因为有时我们往往需要修改一些值，我们不能无限制地创建新值

在实际中我们只能尽量避免在并行算法中修改数据

关键段：是不允许多线程同时执行的操作（通常是修改在多线程中共享的数据的操作） （也就是互斥执行的操作）

同步技术能够保证互斥操作，它有三种实现途径：

1. spin lock 用spin lock保护关键段，不暂停其他线程，让它们持续检测关键段有没有被执行完（是否还有lock）
2. block lock （mutex）将线程都暂停，等执行关键段的线程执行完关键段再继续其他线程
3. 使用原子的修改操作（被称为不阻塞同步）

cas（compare and swag） 和 faa（fetch and add） 书中讲了它们的实现步骤，可以看出它们也遵循类似read modify write的步骤，我们可以原子化它们

一些练习 等待标答中

Algorithm Analysis

算法分析是指我们对代价的分析，它需要精确且抽象，为此有两种技术

1. 渐进分析 （和算法设计与分析课程中的一样）
2. 代价模型

任何算法分析都需要假定一个代价模型，常见的有两种：基于机器和基于语言的代价模型

基于机器的代价模型：以机器指令的执行时间为单位，也就是说它分析算法执行的机器指令的条数 其中RAM模型为单处理器的，PRAM模型为多处理器的（要求多个处理器执行同一算法，但可能是对不同的数据进行处理，处理器之间根据pid进行区分）

RAM模型的弊端：它假定任何机器指令的执行时间是相同的，同时我们有时很难将现代的高级语言转化为机器指令进行分析

PRAM模型的弊端：包含RAM的弊端，且设计并行算法，让所有处理器做相同的操作来达到计算目的是很困难的

本书不使用PRAM模型，也就是考虑代价时分别对单个处理器进行分析

基于语言的代价模型设计了一个函数将特定语言的表达式映射为代价，这种函数通常是递归的

本书使用的基于语言的代价模型是Work-Span模型

v表示变量，Eval(e)表示计算表达式e，[v/x]e表示将v代入e中出现的x中

\(\overline{P}=\frac{W}{S}\)表示并行性，也可据此大致推断用多少处理器比较好

当我们使用Work-Span的代价模型时，我们完全忽略了调度问题而专心设计算法

调度问题是指如何将将并行算法的计算分配给处理器

我们只介绍一种调度算法：贪心调度算法\(\rightarrow\)每当有一个处理器空闲且有一个待计算的任务，就将这个任务分配给这个处理器

使用贪心调度算法，所需时间周期\(T_P\)有上界，这是一个很好的性质

上述性质说明了两件事：

1. \(T_P\)介于理论所需最少的时间周期的\([1,2)\)倍
2. 并行性越高，贪心调度的效果越好

证明1：

证明2：

以上分析没有考虑调度算法的代价，但这是不符合实际的

Probability Theory

讲了离散概率论，内容和概率论一样

引入飞镖游戏，飞镖游戏中的环数是一个\([0,1]\)的连续变量，加入我们原来的问题规模为n，飞镖游戏扔中了0.6，那么我们的问题规模就变为0.6n，当问题规模缩小为1时，飞镖游戏停止

同时我们要猜测总计要扔多少次飞镖，猜中（扔的飞镖数小于等于我们猜的数字）没有惩罚，猜错就有基于问题规模n的一个函数的(例如n、\(n^2\))惩罚

我们的目标是设计一种策略让惩罚的期望小于1

对于这种情况，定义\(R=\frac{1}{r}\),那么飞镖游戏结束时需要扔中\(\log_{R}{n}\)次飞镖，扔飞镖的过程满足多项式分布，故当游戏结束时，总计扔飞镖的次数的数学期望为\(\frac{\log_{R}{n}}{p}\),但显然直接用数学期望的值来猜并不保险，我们的策略是给这个值乘一个大于1的常数k来使惩罚的期望小于1，接下来要计算k取多少合适

首先了解一下Markov 不等式

之后了解一下Chernoff bounds，它是说，T为一随机变量，u为它的数学期望，对常数\(δ\),有下式成立，证明很复杂，参考别人写的博客吧(当然这个不等式是有使用条件的，原文中通过一些设置使得接下来讨论的随机变量满足使用条件)

第一个不等式说明了随机变量的取值小于(1-\(δ\))倍的数学期望的概率

我们用Chernoff bounds计算k，假设T为扔\(k\frac{\log_{R}{n}}{p}\)次飞镖命中的次数，取\(δ=0.5\)，那么

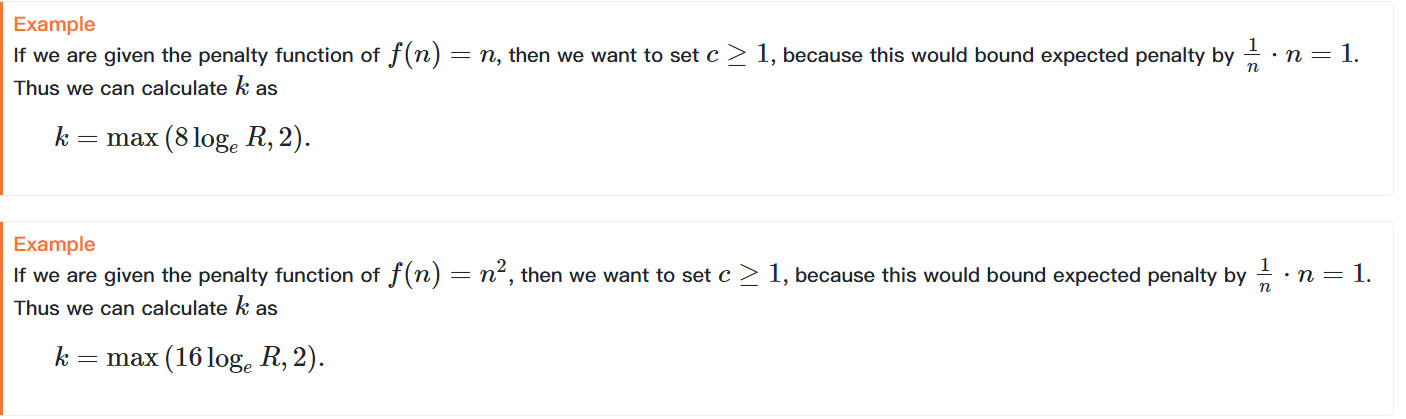
得到上式之后，如果我们代入k=2，就可以看出对于k=2，我们有小于\(\frac{1}{n^c}\)的概率猜错而获得惩罚

那么k>2时，该结论一定也成立，所以我们有了\(k\ge2\)时一个获得惩罚的概率的上界

\(penalty=\frac{1}{n^c}*f(n) \leq 1\)

使用这个公式计算k即可

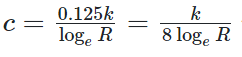
对于这种飞镖游戏，问题规模大小的分析一般依次计算扔1、2、3......次飞镖的期望，规模的期望之间满足递推关系

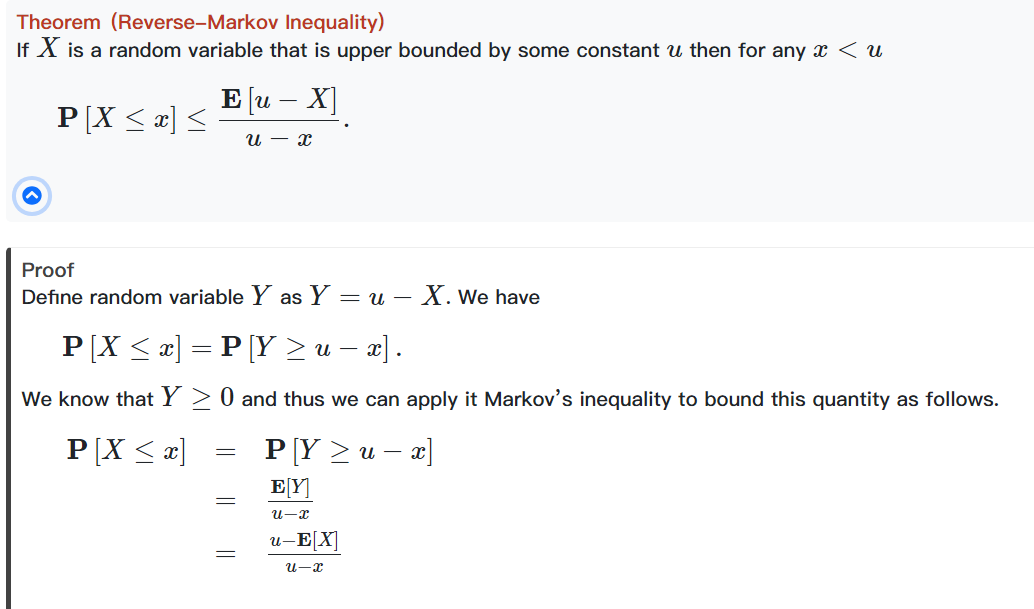
接着了解一下 Reverse Markov 不等式，通过Markov 不等式可以得到它(原文中的下面两个等号应该是小于等于号)

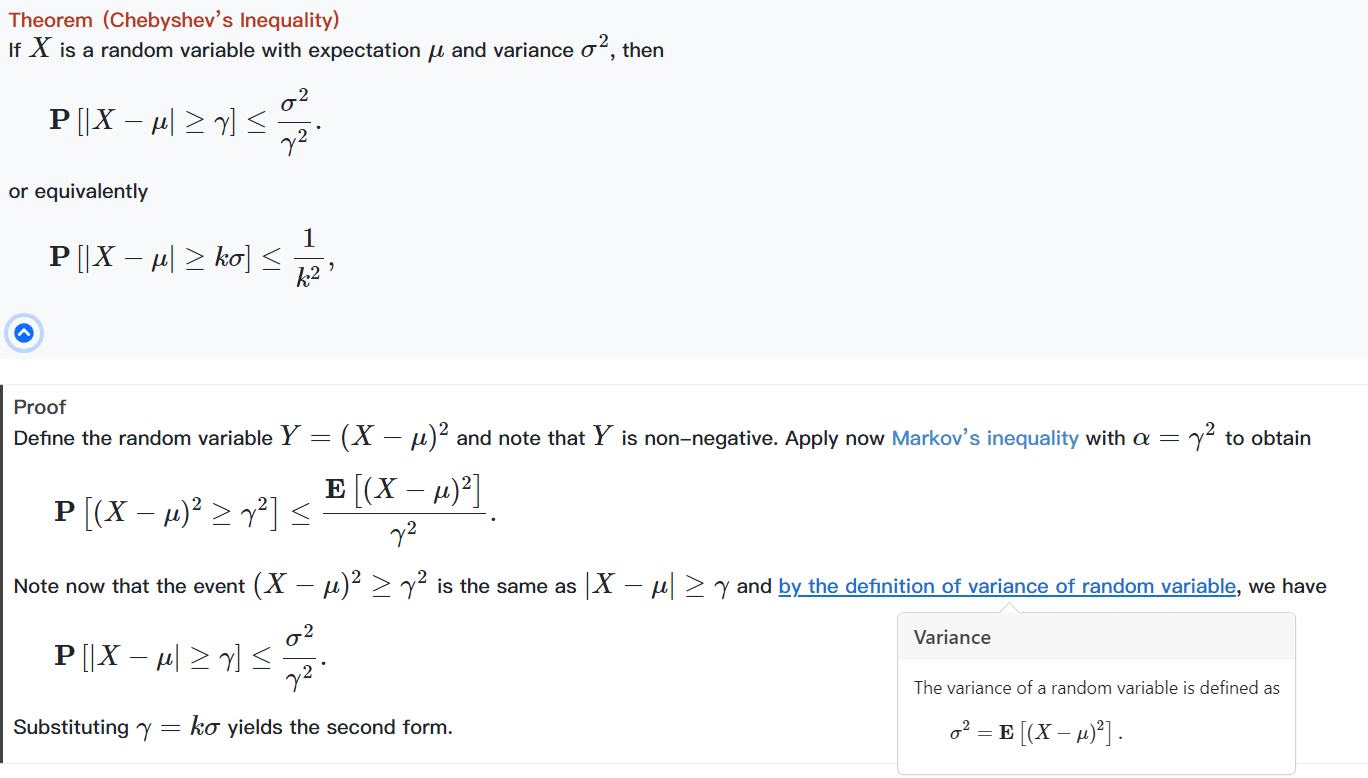
切比雪夫不等式阐释了一个随机变量在其方差的控制下缓慢地偏离其均值的规律,证明同样用到了Markov不等式

当我们不知道飞镖游戏的概率分布，只知道每次问题缩小比例的期望值，可以设计一个新的飞镖游戏(概率分布确定)来拟合原有的飞镖游戏，具体方法略

Sequences

ADT（抽象数据结构）包含对一种数据类型和相应的函数（对其的操作）的定义，但不包含其实现方法

本章就介绍ADT for sequence ，一些操作的代价，以及在给定代价之下的实现方法

我们将\(\alpha\)序列定义为一个定义域为从0开始的连续正整数集到集合\(\alpha\)的映射函数

对\(\alpha\)序列的操作有如下,给出了这些函数的映射关系，接下来会逐个介绍各函数有什么用

简单的函数不作介绍

• 注意nth(2)的返回值为a[2],而序列从0开始
• tabulate以一个函数f，一个正整数n为参数，返回\(<f(0),f(1),f(2),\dots,f(n-1)>\),所有元素是并行计算的
• map顾名思义，以一个函数f，一个序列\(\alpha\)为参数，用f对\(\alpha\)的每个元素进行映射，返回一个\(\beta\)序列，它也是并行计算的
• filter以一个函数f，一个序列\(\alpha\)为参数，对\(\alpha\)的每个元素判断f(a)是否为true，返回一个判断结果为true的元素的序列，保持这些元素的相对顺序，它也是并行计算的
• subsequence三个参数：序列\(\alpha\),下标 i,长度 j，取序列\(\alpha\)从下标从i开始的j个元素
• 在操作序列时，常常将序列分为head和剩下的部分(仍是一个序列)，或者tail和其他部分，这是一种归纳式的处理，许多算法采用这种方式进行设计
• append (a,b)在序列a的后面加上序列b
• flatten依照次序将一个序列的序列变成一个序列
• update(a,(i,x)),将a序列的下标为i的元素的值更新为x
• inject更新多个序列多个位置的值，inject有两个参数，待修改的a序列，和一个记载修改信息的b序列，b序列的元素是(下标，值)的有序对，当有多个下标是相同的，那么只有第一个更新会生效
• 我们依次记下inject对a序列的所有位置的更改次数，并取其最大值作为inject操作的度
• collect函数将一个元素为(key,value)的序列，变成一个元素为(key, value sequence)的序列，做法是以一个cmp函数和原始序列为参数，cmp函数要求能对两个key进行比较得到{less,equal,greater}中的一个值，根据cmp函数的结果，将原始序列中的元素进行分组排序，也就是说key相同的所有value值会被collect为一个value sequence(仍然保持在原始序列中的相对顺序)，接着是下一个key和对应的value sequence，以此构成一个新的序列（有点类似与SQL中的GROUP BY）
• 
• iterate函数对整个序列进行迭代，它有三个参数:函数f,一个值x,序列a，函数f是一个需要两个参数的函数,iterate函数是串行的
• 迭代的过程就是
• 1. 计算f(当前的x , 序列开头的元素)作为新的x
• 1. 将序列a更新为去掉head的剩下的部分，
• 1. 回到第一步，直至迭代完整个序列
• iteratePrefix函数有点类似，但iterate返回x，iteratePrefix返回一个有序对(序列，x)，序列包含所有的中间结果(x的值)
• reduce函数有三个参数:满足结合律的函数f，函数f的左单位元id，序列a，函数f同样需要两个参数，它可以并行
• 
• 
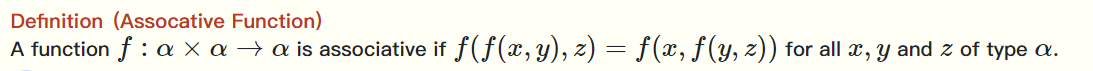
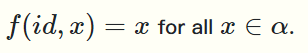
• reduce函数的递归定义很容易理解
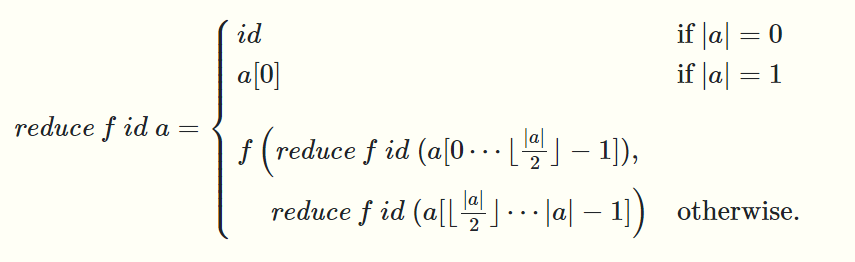
• iterate能够获得计算的中间结果(比如求和过程中的特定前缀和)，而reduce不能，因为它是并行的，我们设计scan函数使得它既并行又能获得中间结果，这样让它看起来像是iterate了一遍，但实际上我们用了并行
• scan的输入和reduce一样，但它对序列a的每个前缀调用一边reduce，返回值和iteratePrefix的形式一样
• scanI与scan类似，此处略

原文中函数定义时使用的":"符号表示定义域，它规定了参数的形式，例如

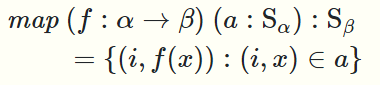
规定f的定义域是包含所有从\(\alpha\)到\(\beta\)的映射的集合，a的定义域是\(\alpha\)序列，map的值的定义域是\(\beta\)序列

一些记号

上面已经给出了操作的定义，接下来简单讲一讲如何用array数据结构去实现它们

我们的做法是设计并实现一系列原始函数，用它们实现要实现的所有函数

原始操作有:

其他函数可以容易地调用这些函数实现，具体参考原教材，这里举个例子

map函数可以通过调用tabulate nth length函数实现(使用了我们规定的记号)

下面给出原始函数的实现方法

我们用一个长的数组和一个left值，一个right值来实现序列，使得序列的内容是数组下标从left到right的元素的内容(这样更方便实现length和subseq)

1. nth 直接去除数组中对应的值 Work 和Span都是常数
2. length=right-left+1 Work 和Span都是常数
3. subseq 修改right和left的值 Work 和Span都是常数
4. \(tabulate\ f\ n\) 创建一个新的长度为n的数组,并行地计算f(0),f(1),...f(n-1),填入到新数组中，Work为总的计算量，Span为max{ f(i) , i \(=1，2，\dots,n-1\) }
5. \(flatten\ a\)，将a序列<sequence,sequence,...,sequence>展开，过程是，用一个Scan并行计算下标，然后将所有元素按下标并行写入一个新的序列，\(\lvert a \rvert\)表示a序列包含多少个sequence，\(\lVert a \rVert\)表示a序列包含的sequecne的元素个数的总和，Scan过程的Work为O(\(\lvert a \rvert\)),Span为O(\(lg\lvert a \rvert\)),写入过程Work为O(\(\lVert a \rVert\)),Span为常数
6. \(inject\) \(a\) \(b\)对序列a进行\(\lvert b \rvert\)次update操作，我们的实现方法是：创建一个新的序列aa
   
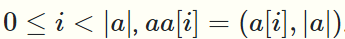
   这样我们就能对每个元素都记录修改了它的是inject的第几个update
   
   注意这里aa初始的元素是a中的元素后面都跟着一个a序列的长度，这时因为只要\(\lvert b \rvert > \lvert a \rvert\),\(inject\)的度就会大于1
   
   然后要做的就是对aa并行地作b中的所有update，对于b中的第k个update我们用一个原子操作来完成(原子操作意味着这个操作里面的指令只能按顺序执行而不能插入其他并行操作的指令)
   
   
   
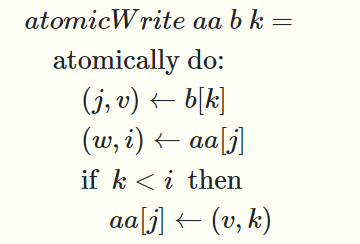
   它将b中的第k个元素读到(j,v)中(也就是要修改下标为j的元素的值为v)，然后将aa的第j个元素的值读到(w,i)中，检查k是否小于i，如果小于就修改同时更新i为k，这样就能保证最终对于a中同一元素排在前面的update生效
   
   显然\(inject\)的Work为O(\(\lvert b \rvert + \lvert a \rvert\))，假设\(inject\)操作的度为\(d\),因为是并行的且update的顺序是随机的，Span的期望为O(\(lg{d}\)) (假如我们有1~d 个修改待执行，每当我们执行一个修改i，就意味着问题规模缩小为 1~i ，这很类似我们之前提到的飞镖游戏，我们只需要投掷O(\(lg{d}\)) 次飞镖)
7. ninject不要求排在前面的update生效，它是随机的 (???)

上一节我们分析了array sequence的原始函数的实现方法并知道了它们的代价，参照教材中其他函数调用原始函数的过程，array based sequence的所有函数的代价就可以轻易地推导出来了

具体可以参照教材array based sequence的cost 表

注意像iterate、reduce、scan这样的函数的代价分析还和序列的计算顺序有关

例如

我们只是改变了序列的顺序，由于中间值的不同，work也是不同的

\(\tau(iterate\ f\ v\ a)\)表示\(iterate\) 过程中对\(f\)的所有调用

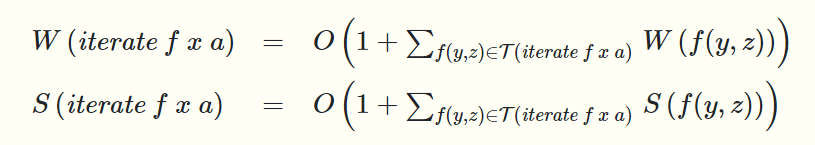
同样reduce的计算顺序不同也会影响cost

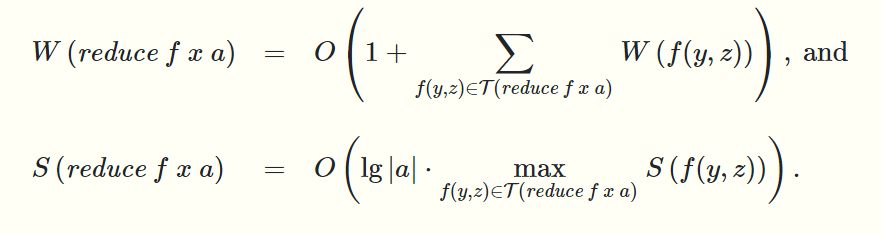
scan和reduce类似，毕竟它是多个reduce同时做

tree sequence 和list sequence 的代价表也在教材中给出

1. 注意tree sequence 的nth和append的代价和array不同前者变为O(lg|a|)的Work和Span，后者变为1+|lg(|a|/|b|)|的Work和Span (\(append\ a\ b\)),用到nth的函数的Work 和Span也要相应地改变
2. list sequence 的 nth a i 的Work 和Span变为了 i，subseq (i,j) 的Work 和Span变为了 1+i ，list sequence 整体是 array sequence 的劣化版(它几乎完全不并行)，我们称之为 array sequence的代价 dominate list sequence 的代价

当函数有多个变量时，我们要用到flatten函数，但有时它是隐式的，计算代价时要注意考虑flatten的代价

素数筛的例子略

我们之前的实现都是pure的，没有修改过数据，但这样每当出现update操作时我们就要将序列copy一边，这样会带来更多的代价

如果一组数据至多会被用到一次，那么我们可以在其上进行修改，因为修改就用到了这组数据，也就表示这组数据再也不会被用到，那么可以随便改，这种数据的使用特征被称为linear的

这种被称作短期数据结构，对它的操作不pure，虽然简化了修改的工作量，但是并行算法中这样的数据结构并不安全

单线程序列统一了两者的优点，在单线程序列种我们使用串行的直接修改，且单线程序列可以与正常序列并行地相互转化(copy)，对于单线程序列我们设计了5种操作

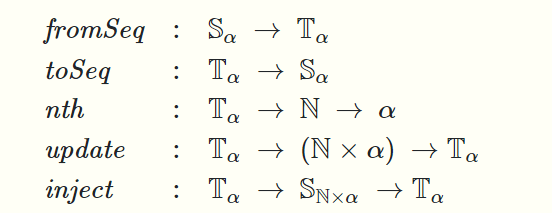
其中\(S_\alpha表示正常的\alpha 序列，T_\alpha 表示 单线程\alpha序列\)，\(fromSeq表示转化为单线程序列，toSeq表示转化为正常的序列\)

代价表

在单线程序列上执行nth和update以及inject明显快很多

tree sequence跳了，应该无所谓吧

Algorithm Design

本节讲算法的设计技术:

1. 两个基本技术: 转化问题 、 暴力搜索
2. 分治
3. 收缩(缩小问题规模递归求解)

在后续章节会讲随机算法和动态规划

转化问题:是讲问题A转化为一个或多个问题B进行求解，然后用求解的问题B的结果得到问题A的结果

通常我们要转化为的问题B是已经有了解法的

输入和输出转化的总代价与解决所有问题B的总代价渐近相同，那么称之为一个efficient的转化

这种技术在基因测序那一节已经用到过了(暴力搜索也在那一节有用到)

分治算法有三步

1. 将问题分解为规模更小的一些子问题
2. 递归地解决这些子问题(设计解决基本情况的算法，也就是递归边界)
3. 组合这些子问题的解来得到原问题的解

它的Work和Span为

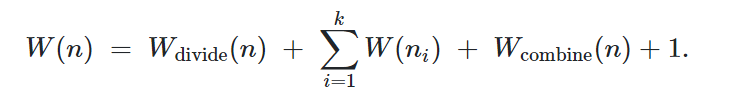
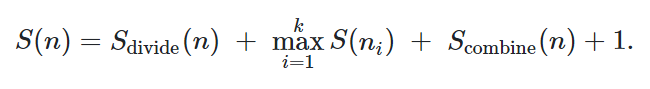
一些使用实例:求最大值，归并排序，使用Scan 进行的求和，欧几里得旅行商问题，Reduce

归并排序中

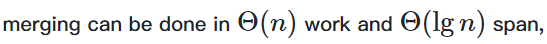
实现方法为：

据此计算归并排序的代价

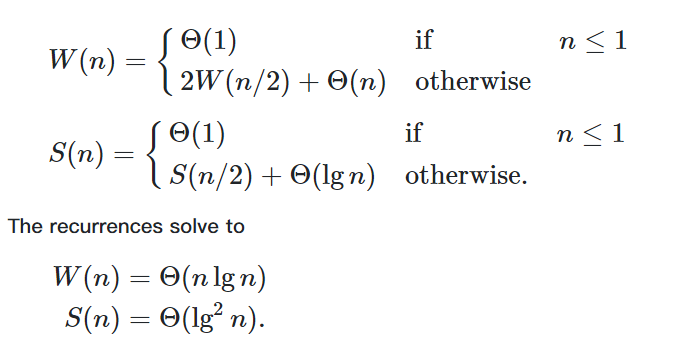
使用Scan 进行的求和，我们可以将序列分成两半，然后并行求其Scan的结果，将后一半的结果都加上前一半的和，将结果拼起来就是整个Scan的结果了，基本情况(递归边界)就是序列长度为0或1

代价分析

欧几里得旅行商也就是平面上的旅行商问题：权重为平面上的点的欧式距离(\(\ell_2\))，找到一种恰好经过所有点一次的权重和最小的路径

分治的方法是:选出x，y中数据跨度大的那个纬度(在该维度下的投影相距最远的两点决定其跨度)，在其跨度的中点进行分割，然后求解子问题，子问题求解完之后，在左右各选一条边去除选择一种连接方式将左右连起来，作为原问题的解(在选边连接的过程中要取代价最小的方式)

收缩:

1. 将问题规模缩小
2. 递归地求解子问题(设计基本情况的解法，也就是递归边界)
3. 子问题的结果扩展到原问题

一些使用实例:求最大值、reduce、scan

具体略

最大连续子序列和考虑使用暴力搜索、收缩、分治来求解，具体略

(算法设计学过)

Randomization

随机算法做随机选择

有两类随机算法，一类用随机选择来安排计算进而减少代价的期望(随机选择与算法的结果无关)，另一类用随机选择来增加算法正确性的期望(随机选择和算法的结果有关)

随机算法的优缺点分析略

给出两个定义：

当，我们称之为high probability，它代表者问题规模无限大时某一情况必然发生，那么它就是high probability

Expected bounds 为算法所做的所有随机选择的代价的平均值

Expected bounds有助于我们分析Expexted Work

而high probability 有助于我们分析Expected Span(Expected Span 往往与随机变量期望的最大值有关，我们可以用high probabilty来确定一个上界，高于这个界的情况high unlikely发生，这样我们就可以用这个界来分析Expected Span了)

随机算法的使用实例：顺序统计量、快排

顺序统计量的算法



随机选择p，将序列按p进行划分为\(l\),\(r\)，然后查找k所在的那一部分，这种技术是收缩

我们可以使用飞镖游戏来分析这个算法的代价

也可以直接分析其问题规模的期望的递推关系，根据问题规模的来计算代价

这里我给出另外一个例子来帮助理解直接分析随机算法的Work和Span(Exercises 8.2)





看懂这里的证明就能看懂书上的分析过程了

快排的算法



这里用到了filter函数的记号，注意\(a_1,a_2,a_3\)的filter是并行的,quicksort \(a_1\) quicksort \(a_2\)也是并行的

pivot的选择对这个算法的效率有很大的影响

当我们随机选择pivot时，可以证明期望的Work为Θ(nlgn)，Span为Θ(lgn)

证明和之前的证明也十分类似，飞镖游戏或直接分析

还可以写递归式来分析quicksort的Work和Span的期望值

Y(n)表示\(quicksort\) n个元素所用的比较的次数，X(n)表示集合\(a_1\)的规模，也就是小于pivot的部分的规模

那么左右两边加上E[],进行分析

之后猜测Work的数量级并用替代法证明猜测成立即可(算法设计与分析里的方法) ，Tips:猜测为O(nlgn)用替代法尝试证明等式成立

同理Span也可以这样进行分析 ，只不过将递推式换为

而\(X(n)\)表示两个子问题中规模大的那个的规模

Binary Search Trees

本节介绍二叉搜索树(BST)，这种数据结构可以用来实现集合(Set)、表(Table)等ADT

BST对基于某种顺序的搜索很有用，而且当我们要求数据是persistent时用BST是很好的(persistent不允许update数据，而BST一般支持插入、删除、搜索)

相较于数组的搜索O(1),插入O(n),BST的搜索是O(lgn),插入也是O(lgn)，实现了一种平衡

但是对于并行算法，我们要对BST设置新的操作来实行并行地插入、删除、搜索

我们要做的工作是:首先定义BST，然后定义ADT（Set、Table），给出如何用BST实现ADT的一些并行的批量操作（求并集，filter等），这个过程只需要实现joinMid操作，然后给出如何保持BST的近似平衡(以Treaps为例，它是一种近似平衡的BST,这种数据结构能够自然地使用并行算法)

BST的定义略

注意这里假设只有内部节点有值，叶子节点是没有值的

分别表示树T的所有元素的值都小于k，都大于k ,T1中的任一元素都小于T2中的任一元素

我们用split joinM joinPair来实现ADT定义的其他操作，且split 和 joinPair可以通过joinM来实现

前面简单的操作的含义不再赘述

union为取并集，intersection取交集，difference取包含在T1中但不在T2中的元素，注意这三个操作都以两个BST为参数返回一个新的BST且它们是通过并行实现的

split T k 将树T分为两棵树 T1、T2，满足\(T1<k ,T2>k\)，同时返回一个布尔值表示k是否出现在T中，不指定新的两棵是什么类型的BST

JoinPair T1 T2 将满足T1< T2的两棵树合并为一棵新的树

JoinM T1 k T2 将满足\(T1< k <T2\)的两棵树和一个值合并为一棵新的树

expose函数判断T的根是内部节点还是叶子，如果是内部节点就返回(L,k,R)，如果是叶子就返回空值

JoinMid函数做了使BST保持近似平衡的工作,它以代表叶子的空值或者(L,k,R)为参数，返回一个叶子或者平衡完的内部节点

为了在O（1）的Work中实现size（T），在树的每个节点存储子树的大小(expose 不返回这部分值，但JoinMid平衡时要更新它)

这里要实现的ADT以Set为例(每个节点只包含一个key)，但是可以通过简单地在节点中添加对应value值实现Table