DL4NLP——词表示模型（二）基于神经网络的模型：NPLM；word2vec（CBOW/Skip-gram）

本文简述了以下内容：

神经概率语言模型NPLM，训练语言模型并同时得到词表示

word2vec：CBOW / Skip-gram，直接以得到词表示为目标的模型

（一）原始CBOW(Continuous Bag-of-Words)模型

（二）原始Skip-gram模型

（三）word analogy

神经概率语言模型NPLM

上篇文简单整理了一下不同视角下的词表示模型。近年来，word embedding可以说已经成为了各种神经网络方法（CNN、RNN乃至各种网络结构，深层也好不深也罢）处理NLP任务的标配。word embedding（词嵌入；词向量）是指基于神经网络来得到词向量的模型（如CBOW、Skip-gram等，几乎无一例外都是浅层的）所train出来的词的向量表示，这种向量表示被称为是分布式表示distributed representation，大概就是说单独看其中一维的话没什么含义，但是组合到一起的vector就表达了这个词的语义信息（粒度上看的话，不止词，字、句子乃至篇章都可以有分布式表示；而且，例如网络节点、知识图谱中的三元组等都可以有自己的embedding，各种“xx2vec”层出不穷）。这种基于神经网络的模型又被称作是基于预测（predict）的模型，超参数往往要多于基于计数（count）的模型，因此灵活性要强一些，超参数起到的作用可能并不逊于模型本身。尽管有一批paper去证明了这类神经网络得到词表示模型的本质其实就是矩阵分解，但这并不妨碍它们的广泛应用。

下面就简要介绍利用神经网络来得到词表示的非常早期的工作——神经概率语言模型（NPLM, Neural Probabilistic Language Model），通过训练语言模型，同时得到词表示。

语言模型是指一个词串 $\{w_t\}_{t=1}^T=w_1^T=w_1,w_2,...,w_T$ 是自然语言的概率 $P(w_1^T)$ 。 词$w_t$的下标 $t$ 表示其是词串中的第 $t$ 个词。根据乘法公式，有

$$P(w_1,w_2,...,w_T)=P(w_1)P(w_2|w_1)P(w_3|w_1,w_2)...P(w_T|w_1,w_2,...,w_{T-1})$$

因此要想计算出这个概率，那就要计算出 $P(w_t|w_1,w_2,...,w_{t-1}),t\in \{1,2,...,T\}$ 。传统方式是利用频数估计：

$$P(w_t|w_1,w_2,...,w_{t-1})=\frac{\text{count}(w_1,w_2,...,w_{t-1},w_t)}{\text{count}(w_1,w_2,...,w_{t-1})}$$

count()是指词串在语料中出现的次数。暂且抛开数据稀疏（如果分子为零那么概率为零，这个零合理吗？如果分母为零，又怎么办？）不谈，如果词串的长度很长的话，这个计算会非常费时。n-gram模型是一种近似策略，作了一个 $n-1$ 阶马尔可夫假设：认为目标词 $w_t$ 的条件概率只与其之前的 $n-1$ 个词有关：

$$\begin{aligned}P(w_t|w_1,w_2,...,w_{t-1})&\approx P(w_t|w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1})\\&=\frac{\text{count}(w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1},w_t)}{\text{count}(w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1})}\end{aligned}$$

神经概率语言模型NPLM延续了n-gram的假设：认为目标词 $w_t$ 的条件概率与其之前的 $n-1$ 个词有关。但其在计算 $P(w_t|w_1,w_2,...,w_{t-1})$ 时，则使用的是机器学习的套路，而不使用上面count()的方式。那么它是如何在训练语言模型的同时又得到了词表示的呢？

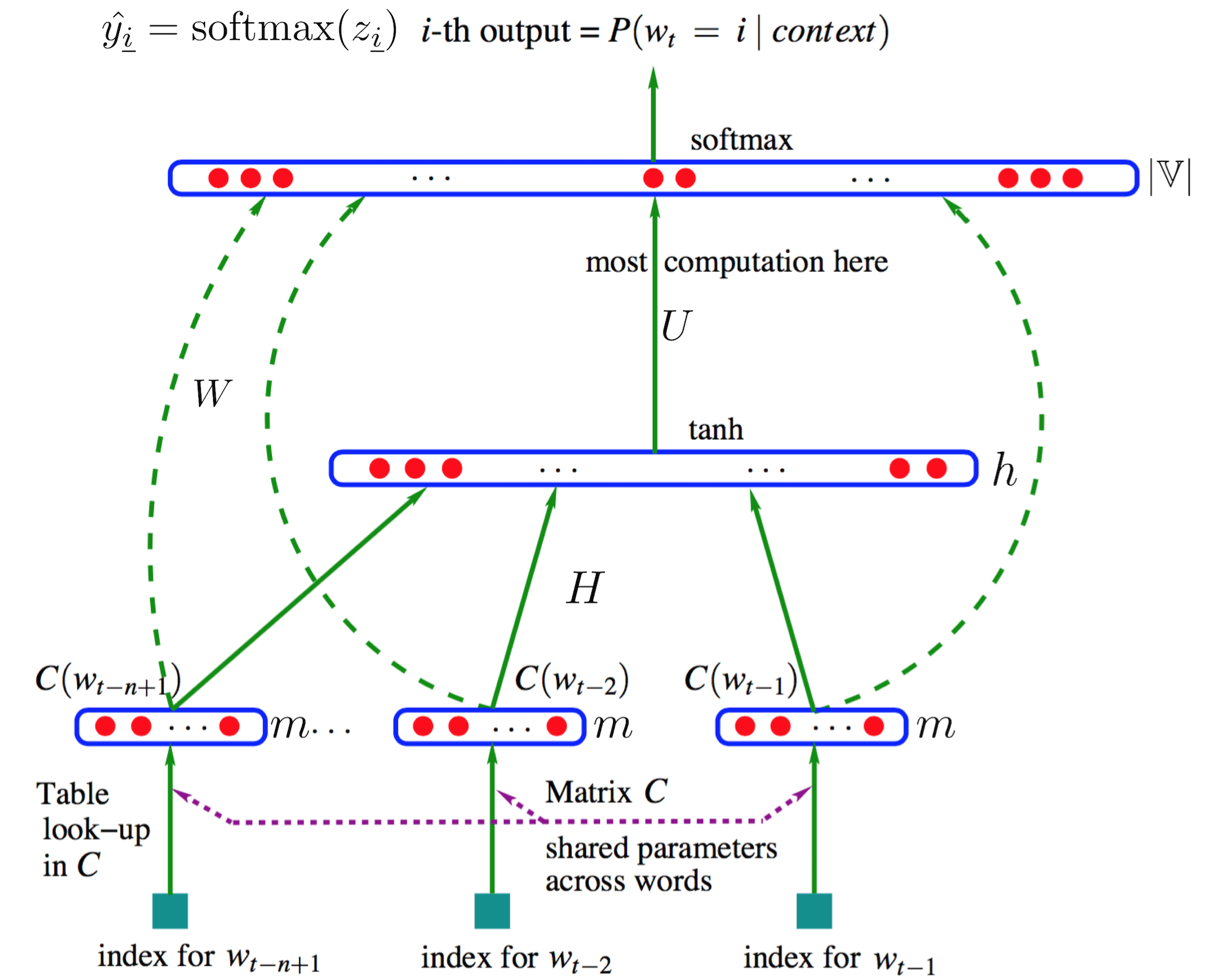
图片来源：[1]，加了几个符号

设训练语料为 $\mathbb D$ ，提取出的词表为 $\mathbb V=\{w_{\underline 1},w_{\underline 2},...,w_{\underline{|\mathbb V|}}\}$ 。词 $w_{\underline i}$ 的下标 $\underline i$ 表示其是词表中的第 $i$ 个词，区别于不带下划线的下标。大致说来，NPLM将语料中的一个词串 $w_{t-(n-1)}^t$ 的目标词 $w_t$ 之前的 $n-1$ 个词的词向量（即word embedding，设维度为 $m$ ）按顺序首尾拼接得到一个“长”的列向量 $\boldsymbol x$ ，作为输入层（也就是说共 $(n-1)m$ 个神经元）。然后经过权重矩阵 $H_{h\times (n-1)m}$ 来到隐层（神经元数为 $h$ ），并用tanh函数激活。之后再经过权重矩阵 $U_{|\mathbb V|\times h}$ 来到输出层（神经元数当然为 $|\mathbb V|$ ），并使用softmax()将其归一化为概率。另外存在一个从输入层直连输出层的权重矩阵 $W_{|\mathbb V|\times (n-1)m}$ 。所以网络的输出如下（隐层和输出层加了偏置）：

$$\boldsymbol z=U\tanh (H\boldsymbol x+\boldsymbol d)+\boldsymbol b+W\boldsymbol x$$

$$\hat y_{\underline i}=P(w_{\underline i}|w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1})=\text{softmax}(z_{\underline i})=\frac{\exp z_{\underline i}}{\sum\limits_{k=1}^{|\mathbb V|}\exp z_{\underline k}},\quad w_{\underline i}\in \mathbb V$$

$\hat y_{\underline i}$ 表示目标词是词表中第 $i$ 个词 $w_{\underline i}$ 的概率。

$\exp z_{\underline i}$ 表示前 $n-1$ 个词对词表中第 $i$ 个词 $w_{\underline i}$ 的能量聚集。

词表中的每个词的词向量都存在一个矩阵 $C$ 中，look-up操作就是从矩阵中取出需要的词向量。由此可以看出，NPLM模型和传统神经网络的区别在于，传统神经网络需要学习的参数是权重和偏置；而NPLM模型除了需要学习权重和偏置外，还需要对输入（也就是词向量）进行学习。

那么，模型的参数就有：$C,U,H,W,\boldsymbol b,\boldsymbol d$ 。

使用交叉熵损失函数，模型对目标词 $w_t$ 的损失为

$$\mathcal L =-\log \hat y_t=-\log P(w_t|w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1})=-\log \text{softmax}(z_t) $$

那么模型的经验风险为（省略了常系数）

$$ \begin{aligned} \mathcal L&=-\sum_{w_{t-(n-1)}^t\in \mathbb D}\log \hat y_t\\&=-\sum_{w_{t-(n-1)}^t\in \mathbb D}\log P(w_t|w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1})\\&=-\sum_{w_{t-(n-1)}^t\in \mathbb D}\log \text{softmax}(z_t)  \end{aligned} $$

所以接下来就可以使用梯度下降等方法来迭代求取参数了。这样便同时训练了语言模型和词向量。

word2vec：CBOW / Skip-gram

上面介绍的NPLM以训练语言模型为目标，同时得到了词表示。2013年的开源工具包word2vec则包含了CBOW和Skip-gram这两个直接以得到词向量为目标的模型。

像SGNS这些新兴的获得embedding的模型其实不属于字面含义上的“深度”学习，因为这些模型本身都是很浅层的神经网络。但得到它们后，通常会作为输入各种神经网络结构的初始值（也就是预训练，而不采用随机初始化），并随网络参数一起迭代更新进行fine-tuning。就我做过的实验来说，预训练做初始值时通常可以提升任务上的效果，而且fine-tuning也是必要的，不要直接用初始值而不更新了。

首先它获取word embedding（Distributed representation）的方式是无监督的，只需要语料本身，而不需要任何标注信息，训练时所使用的监督信息并不来自外部标注；但之前的pLSA什么的也是无监督的啊，也是稠密向量表示啊。所以我觉得word2vec之所以引爆了DL在NLP中的应用更可能是因为它在语义方面的一些优良性质，比如相似度方面和词类比（word analogy）现象，便于神经网络从它开始继续去提取一些high level的东西，进而去完成复杂的任务。

这里先介绍两种模型的没有加速策略的原始形式（也就是输出层是softmax的那种。对于Skip-gram模型，作者在paper中称之为“impractical”），两种加速策略将在下篇文中介绍。

与NPLM不同，在CBOW / Skip-gram模型中，目标词 $w_t$ 是一个词串中间的词而不是最后一个词，其拥有的上下文（context）为前后各 $m$ 个词：$w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m}$ 。NPLM基于n-gram，相当于目标词只有上文。后文中，“目标词”和“中心词”是同一概念，“周围词”和“上下文”是同一概念。

在原始的CBOW / Skip-gram模型中，任一个词 $w_{\underline i}$ 将得到两个word embedding（设维度为 $n$ ）：作为中心词时的词向量，也称为输出词向量 $\boldsymbol v_{\underline i}\in \mathbb R^{n\times 1}$ ；以及作为周围词时的词向量，也称为输入词向量 $\boldsymbol u_{\underline i}\in \mathbb R^{n\times 1}$ 。词向量的下标和词的下标相对应，比如说目标词 $w_t$ 的词向量就对应为 $\boldsymbol v_t$ 和 $\boldsymbol u_t$ 。

与NPLM类似，词表中每个词的词向量都存在一个矩阵中。由于存在两套词向量，因此就有两个矩阵：输入词矩阵 $V_{n\times |\mathbb V|}=[\boldsymbol v_{\underline 1},...,\boldsymbol v_{\underline {|\mathbb V|}}]$ ，其每一列都是一个词作为周围词时的词向量；输出词矩阵 $U_{|\mathbb V|\times n}=[\boldsymbol u_{\underline 1}^\top ;...;\boldsymbol u_{\underline {|\mathbb V|}}^\top]$ ，其每一行都是一个词作为中心词时的词向量。比如说若想取出词作为周围词时的词向量，只要知道词在词表中的编号即可，取出的操作相当于用输入词矩阵乘以词的one-hot representation。

（一）CBOW(Continuous Bag-of-Words)

不带加速的CBOW模型是一个两层结构，相比于NPLM来说CBOW模型没有隐层，通过上下文来预测中心词，并且抛弃了词序信息——

输入层：$n$ 个节点，上下文共 $2m$ 个词的词向量的平均值；

输入层到输出层的连接边：输出词矩阵 $U_{|\mathbb V|\times n}$ ；

输出层：$|\mathbb V|$ 个节点。第 $i$ 个节点代表中心词是词 $w_{\underline i}$ 的概率。

如果要视作三层结构的话，可以认为——

输入层：$2m\times |\mathbb V|$个节点，上下文共 $2m$ 个词的one-hot representation

输入层到投影层到连接边：输入词矩阵 $V_{n\times |\mathbb V|}$ ；

投影层：：$n$ 个节点，上下文共 $2m$ 个词的词向量的平均值；

投影层到输出层的连接边：输出词矩阵 $U_{|\mathbb V|\times n}$ ；

输出层：$|\mathbb V|$ 个节点。第 $i$ 个节点代表中心词是词 $w_{\underline i}$ 的概率。

这样表述相对清楚，将one-hot到word embedding那一步描述了出来。这里的投影层并没有做任何的非线性激活操作，直接就是Softmax层。换句话说，如果只看投影层到输出层的话，其实就是个Softmax回归模型，但标记信息是词串中心词，而不是外部标注。

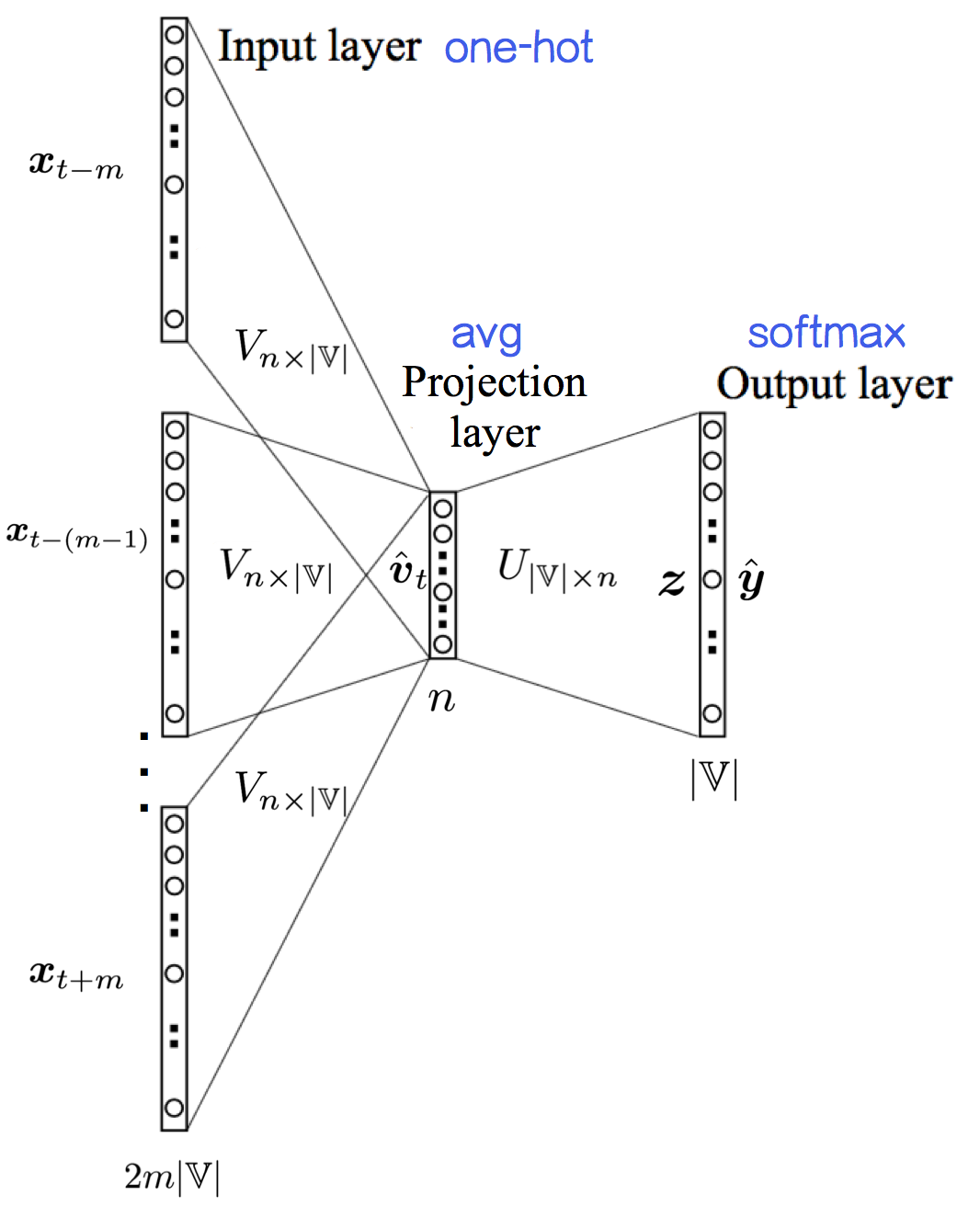
图片来源：[5]，把记号都改成和本文一致

首先，将中心词 $w_t$ 的上下文 $c_t$ ：$w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m}$ 由one-hot representation（ $\boldsymbol x_{t+j}$ ）转为输入词向量（ $\boldsymbol v_{t+j}$ ）：

$$\boldsymbol v_{t+j}=V\boldsymbol x_{t+j},\quad j\in \{-m,...,m\}\setminus \{0\}$$

进而将上下文的输入词向量 $\boldsymbol v_{t-m},...,\boldsymbol v_{t-1},\boldsymbol v_{t+1},...,\boldsymbol v_{t+m}$ 求平均值，作为模型输入：

$$\hat{\boldsymbol v}_t=\frac{1}{2m}\sum_j\boldsymbol v_{t+j},\quad j\in \{-m,...,m\}\setminus \{0\}$$

这一步叫投影（projection）。可以看出，CBOW像词袋模型(BoW)一样抛弃了词序信息，然后窗口在语料上滑动，就成了连续词袋= =。丢掉词序看起来不太好，不过开个玩笑的话：“研表究明，汉字的序顺并不定一能影阅响读，事证实明了当你看这完句话之后才发字现都乱是的”。

与NPLM不同，CBOW模型没有隐藏层，投影之后就用softmax()输出目标词是某个词的概率，进而减少了计算时间：

$$\boldsymbol z=U\hat{\boldsymbol v}_t$$

$$\hat y_{\underline i}=P(w_{\underline i}|w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m})=\text{softmax}(z_{\underline i})=\text{softmax}(\boldsymbol u_{\underline i}^\top \hat{\boldsymbol v}_t),\quad w_{\underline i}\in \mathbb V $$

那么模型的参数就是两个词向量矩阵：$U,V$ 。

对于中心词 $w_t$ ，模型对它的损失为

$$\begin{aligned}\mathcal L&=-\log \hat y_t\\&=-\log P(w_t|w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m})\\&=-\log \text{softmax}(z_t)\\&=-\log \frac{\exp (\boldsymbol u_t^\top \hat{\boldsymbol v}_t)}{\sum_{k=1}^{|\mathbb V|}\exp (\boldsymbol u_{\underline k}^\top \hat{\boldsymbol v}_t)}\\&=-\boldsymbol u_t^\top \hat{\boldsymbol v}_t+\log \sum_{k=1}^{|\mathbb V|}\exp (\boldsymbol u_{\underline k}^\top \hat{\boldsymbol v}_t)\\&=-z_t+\log \sum_{k=1}^{|\mathbb V|}\exp z_{\underline k} \end{aligned}$$

所以模型的经验风险为

$$ \begin{aligned} \mathcal L&=-\sum_{w_{t-m}^{t+m}\in \mathbb D}\log \hat{y_t}\\&=-\sum_{w_{t-m}^{t+m}\in \mathbb D}\log P(w_t|w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m})\\&=-\sum_{w_{t-m}^{t+m}\in \mathbb D}\log \text{softmax}(z_t) \end{aligned} $$

做文本的各位同好应该都知道fastText，它相比于CBOW有两个比较重要的区别：首先，fastText是一个端到端的分类器，用全部窗口词取平均去预测文档的标签，而不是预测窗口中心词；另外一个，是它引入了局部词序，也就是 n-gram 特征，所以train出来的词向量和word2vec有一些不一样的特点。因为Hierarchical Softmax还有其他的trick，它的速度快到难以置信，而且精度并不低，没用过fastText的各位可以跑下实验感受一下。

下面开始是非常无聊的求导练习。。。

如果用SGD来更新参数的话，只需求出模型对一个样本的损失的梯度。也就是说上式的求和号可以没有，直接对 $\mathcal L$ 求梯度，来更新参数。

I. 首先是对输出词矩阵 $U^\top =[\boldsymbol u_{\underline 1},...,\boldsymbol u_{\underline {|\mathbb V|}}]$ ：

这部分和Softmax回归模型的梯度推导过程是一样一样的。有很多种方法，下面介绍最按部就班的方法。

因为 $z_{\underline i}=\boldsymbol u_{\underline i}^\top \hat{\boldsymbol v}_t$ ，所以 $\dfrac{\partial \mathcal L}{\partial \boldsymbol u_{\underline i}}=\dfrac{\partial z_{\underline i}}{\partial \boldsymbol u_{\underline i}}\dfrac{\partial \mathcal L}{\partial z_{\underline i}}=\hat{\boldsymbol v}_t\dfrac{\partial \mathcal L}{\partial z_{\underline i}}$ （这里的 $\dfrac{\partial \mathcal L}{\partial z_{\underline i}}$ 其实就是BP算法中的 $\delta$ ），那么先求 $\dfrac{\partial \mathcal L}{\partial z_{\underline i}}$ ：

(1) 对 $\forall w_{\underline i}\in \mathbb V\setminus \{w_t\}$ ，有 $y_{\underline i}=0$，那么

$$\begin{aligned}\frac{\partial \mathcal L}{\partial z_{\underline i}}&=\frac{\partial (-z_t+\log \sum\limits_{k=1}^{|\mathbb V|}\exp z_{\underline k})}{\partial z_i}\\&=0+\frac{\dfrac{\partial \sum_{k=1}^{|\mathbb V|}\exp z_{\underline k}}{\partial z_{\underline i}}}{\sum\limits_{k=1}^{|\mathbb V|}\exp z_{\underline k}}=\frac{\exp z_{\underline i}}{\sum\limits_{k=1}^{|\mathbb V|}\exp z_{\underline k}}=\hat y_{\underline i}=\hat y_{\underline i}-y_{\underline i}\end{aligned}$$

(2) 对 $w_{\underline i}=w_t$ ，有 $y_{\underline i}=1$，那么

$$\frac{\partial \mathcal L}{\partial z_{\underline i}}=\frac{\partial \mathcal L}{\partial z_t}=-1+\hat y_t=\hat y_{\underline i}-y_{\underline i}$$

可见两种情形的结果是统一的，就是误差项。

因此有

$$\frac{\partial \mathcal L}{\partial \boldsymbol u_{\underline i}}=(\hat y_{\underline i}-y_{\underline i})\hat{\boldsymbol v}_t,\quad w_{\underline i}\in \mathbb V$$

那么对于词表中的任一个词 $w_{\underline i}$ ，其输出词向量的更新迭代式为：

$$\boldsymbol u_{\underline i}=\boldsymbol u_{\underline i}-\alpha(\hat y_{\underline i}-y_{\underline i})\hat{\boldsymbol v}_t,\quad w_{\underline i}\in \mathbb V$$

不妨把它们拼接成对矩阵的梯度：

$$ \begin{aligned}\frac{\partial \mathcal L}{\partial U^\top}&=[\frac{\partial \mathcal L}{\partial \boldsymbol u_{\underline 1}},...,\frac{\partial \mathcal L}{\partial \boldsymbol u_{\underline {|\mathbb V|}}}]\\&=\hat{\boldsymbol v}_t(\hat{\boldsymbol y}-\boldsymbol y)^\top \end{aligned} $$

$$U^\top= U^\top-\alpha\hat{\boldsymbol v}_t(\hat{\boldsymbol y}-\boldsymbol y)^\top$$

II. 接下来是对输入词矩阵 $V=[\boldsymbol v_{\underline 1},...,\boldsymbol v_{\underline {|\mathbb V|}}]$ ：

因为 $\hat{\boldsymbol v}_t=\dfrac{1}{2m}\sum_j\boldsymbol v_{t+j}$ ，所以 $\dfrac{\partial\mathcal L}{\partial \boldsymbol v_{t+j}}=\dfrac{\partial \hat{\boldsymbol v}_t}{\partial \boldsymbol v_{t+j}}\dfrac{\partial \mathcal L}{\partial \hat{\boldsymbol v}_t}=\dfrac{1}{2m}I\dfrac{\partial \mathcal L}{\partial \hat{\boldsymbol v}_t}$，那么求 $\dfrac{\partial \mathcal L}{\partial \hat{\boldsymbol v}_t}$ ：

$$\begin{aligned} \frac{\partial \mathcal L}{\partial \hat{\boldsymbol v}_t}&=\sum_{k=1}^{|\mathbb V|}\frac{\partial \mathcal L}{\partial z_{\underline k}}\frac{\partial z_{\underline k}}{\partial \hat{\boldsymbol v}_t}\\&=\sum_{k=1}^{|\mathbb V|}(\hat y_{\underline k}-y_{\underline k})\boldsymbol u_{\underline k}\\&=[\boldsymbol u_{\underline 1},...,\boldsymbol u_{\underline {|\mathbb V|}}]   \begin{pmatrix} \hat y_{\underline 1}-y_{\underline 1}\\ \vdots \\ \hat y_{\underline{|\mathbb V|}}-y_{\underline{|\mathbb V|}} \end{pmatrix} \\&=U^\top(\hat{\boldsymbol y}-\boldsymbol y) \end{aligned}$$

因此有

$$\frac{\partial \mathcal L}{\partial \boldsymbol v_{t+j}}=\frac{1}{2m}U^\top(\hat{\boldsymbol y}-\boldsymbol y),\quad j\in \{-m,...,m\}\setminus \{0\}$$

那么对于中心词 $w_t$ 的上下文的任一个词 $w_{t+j}$ ，其输入词向量的更新迭代式为：

$$\boldsymbol v_{t+j}=\boldsymbol v_{t+j}-\frac{1}{2m}\alpha U^\top(\hat{\boldsymbol y}-\boldsymbol y),\quad j\in \{-m,...,m\}\setminus \{0\}$$

（二）Skip-gram

不带加速的Skip-gram模型其实和CBOW模型很相似，二者都是用上下文来预测中心词。二者的区别在于，CBOW模型把上下文的 $2m$ 个词向量求平均值“揉”成了一个向量 $\hat{\boldsymbol v}_t$ 然后作为输入，进而预测中心词；而Skip-gram模型则是把上下文的 $2m$ 个词向量 $\boldsymbol v_{t+j}$ 依次作为输入，然后预测中心词。

Skip-gram模型中，对于中心词 $w_t$ ，模型对它的损失为

$$\begin{aligned}\mathcal L&=-\log P(w_t|w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m})\\&=-\log \prod_jP(w_t|w_{t+j})\\&=-\log \prod_j\hat y_t^{(j)}\\&=-\log \prod_j\text{softmax}(\hat z_t^{(j)})\\&=-\sum_j\log \frac{\exp (\boldsymbol u_t^\top \boldsymbol v_{t+j})}{\sum\limits_{k=1}^{|\mathbb V|}\exp (\boldsymbol u_{\underline k}^\top \boldsymbol v_{t+j})}\end{aligned}$$

第二个等号是独立性假设。后面的求梯度过程也是类似的。

下篇博文将简述两种从计算上加速的策略。

观众朋友们可能会问，实验呢？我觉得word embedding的实验还是要结合具体任务，毕竟它通常是作为初始值的。我做实验时都是用gensim包来train词向量，现在TF也有例子，我没对比过。现在感受就是：用pre-train的话比随机初始化要好；fine-tuning做了比不做要好。基本上都属于说了跟没说一样……关于各个超参数的取值，首先我习惯用SGNS（Skip-gram搭配负采样加速），然后诸如维数、窗口大小、最低词频、二次采样的设置等等都要根据语料的实际情况：维数的话，如果不是机器翻译这种特别大的任务一般200以内就够；窗口大小，如果是推特这样的短文本那就不能取太大。调这些参数的trick在网上也有一些其它的博客在写，这里只是笼统的写一点。另外，各个我之前的pre-train都用的是word2vec的，没用过GloVe，如果语料足够大就用语料训练，如果语料不大就用中文维基百科。以后可能会尝试对比一下GloVe做pre-train。

另外我个人有个疑惑，关于word2vec的改进应该有不少paper，如果它们是有效的，为什么没有被写进gensim这样的工具包呢？

（三）word analogy

word analogy是一种有趣的现象，可以作为评估词向量的质量的一项任务。

图片来源：[6]

word analogy是指训练出的word embedding可以通过加减法操作，来对应某种关系。比如说左图中，有 $w(king)-w(queen)\approx w(man)-w(woman)$ 。那么评测时，则是已知这个式子，给出king、queen和man三个词，看与 $w(king)-w(queen)+w(woman)$ 最接近的是否是 $w(woman)$ 。右图则表示，word analogy现象不只存在于语义相似，也存在于语法相似。

参考：

[1] A Neural Probabilistic Language Model, LMLR2003

[2] Efficient Estimation of Word Representations in Vector Space, ICLR2013

[3] CS224d Lecture Notes1

[4] (PhD thesis)基于神经网络的词和文档语义向量表示方法研究

[5] word2vec Parameter Learning Explained

[6] Linguistic Regularities in Continuous Space Word Representations, NAACL2013

[7] Comparison of FastText and Word2Vec