poj_3468: A Simple Problem with Integers （树状数组区间更新）

题目链接： http://poj.org/problem?id=3468　　

　　　题目是对一个数组，支持两种操作

　　　　操作C：对下标从a到b的每个元素，值增加c；

　　　　操作Q：对求下标从a到b的元素值之和。

　　这道题也可以用线段树解，本文不做描述，下面分析如何用树状数组来解决这道题。

　　/*先把问题简化一点，因为 结果=初值+增量，所以，我们可以只对增量进行分析。然后，这种题有一个特点，就是如果对一般的一个操作C与操作查询前缀和的组合符合条件，那么无论进行多少次任意操作结果都是正确的。故 假设，先进行一次参数分别为 l,r,c 的操作C，再进行一次查询前缀和S_i的操作(i 与l r的大小关系不定）。操作C之后，对S_i，①当i<l时，S_i=0，②当l<=i<r时，S_i=c*(i-l+1)，③当i>=r时，S_i=c*(r-l+1)。要使情况①③满足比较简单，只需使add操作不在l左边进行，且对一树状数组的l和r分别进行+x+c*(r-l+1),-x的操作；而分析如何满足情况②，可以把S_i看作是分布在直线y=c(x-l)=cx-cl上的一系列散点，易看出实现+cx的方法，就是在l执行add c的操作，在r执行add -c的操作，查询时查询sum()*x，而实现-cl的方法可以与上面“分别进行+x+c*(r-l+1),-x的操作”（引号中的x是不确定的）联系起来得出。故而任意S_i都可以得出。*/

 #include <cstdio>

 typedef long long LL;

 const int maxn =1e5+;
 LL a[][maxn];
 LL psum[maxn];
 int n;

 inline int lowbit(int x)
 {
     return x&-x;
 }
 void add(LL a[],int x,int d)
 {
     while(x<=n)
     {
         a[x]+=d;
         x+=lowbit(x);
     }
 }
 LL sum(LL a[],int x)
 {
     LL ret=;
     while(x)
     {
         ret+=a[x];
         x-=lowbit(x);
     }
     return ret;
 }

 LL query(int x)
 {
     return sum(a[],x)*x+sum(a[],x);
 }

 int main()
 {
     int q;
     scanf("%d%d",&n,&q);
     for(int i=;i<=n;i++)
     {
         scanf("%I64d",&psum[i]);
         psum[i]+=psum[i-];
     }
     char op[];
     while(q--)
     {
         int l,r;
         scanf("%s%d%d",op,&l,&r);
         if(op[]=='Q')
             printf("%I64d\n",query(r)-query(l-)+psum[r]-psum[l-]);
         else
         {
             int c;
             scanf("%d",&c);
             add(a[],l,c);
             add(a[],r,-c);
             add(a[],l,c*(-l+));
             add(a[],r,c*r);
         }
     }
 }

//上面内容废弃，以下解析为2018.05.30更新

假设数组用a[]表示，定义辅助数组s[]、d[]，其具体含义为

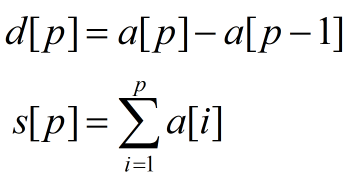
且s[]、d[]间有如下关系

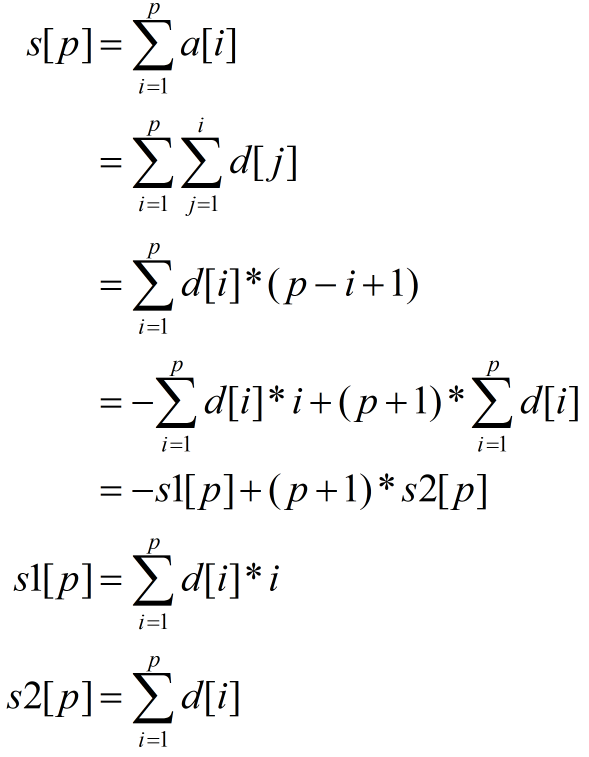
原题中对a[]的区间修改，可以视为对d[]的单点修改，而s[]又可以由d[i]、i*d[i]的前缀和推导出来。且维护s1[]、s2[]较容易，因为每次操作都是对d[]进行单点修改。具体可以参考以下代码

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<functional>
#include<iostream>
#include<cmath>
#include<cctype>
#include<ctime>
using namespace std;
typedef long long LL;

const int N=1e5+;

LL s1[N],s2[N];
int n,q;

inline int lowbit(int x)
{
    return x&-x;
}
void add(LL a[],int i,LL x)
{
    while(i<=n)
    {
        a[i]+=x;
        i+=lowbit(i);
    }
}
LL sum(LL a[],int i)
{
    LL ret=;
    while(i)
    {
        ret+=a[i];
        i-=lowbit(i);
    }
    return ret;
}
void Add(int i,LL x)
{
    add(s1,i,x*i),add(s2,i,x);
}
LL Sum(int i)
{
    return -sum(s1,i)+(i+)*sum(s2,i);
}
int main()
{
    scanf("%d%d",&n,&q);
    for(int i=;i<=n;i++)
    {
        LL t;
        scanf("%lld",&t);
        Add(i,t),Add(i+,-t);
    }
    while(q--)
    {
        int l,r;
        char op[];
        scanf("%s%d%d",op,&l,&r);
        if(op[]=='Q')
            printf("%lld\n",Sum(r)-Sum(l-));
        else
        {
            LL t;
            scanf("%lld",&t);
            Add(l,t),Add(r+,-t);
        }
    }
}