JavaScript: 使用 atan2 来绘制箭头和曲线

最近搞Canvas绘图，知道了JavaScript中提供了atan2(y,x)这样一个三角函数。乍眼一看，不认识，毕竟在高中时，学过的三角函数有：sin,cos,arcsin,arccos,tan,arctan等，并没有这个。而工作中又需要用到它，所以这里就做了个简单的了解。

在坐标系中理解tan 和atan
为何存在atan2 ?
atan2 应用
- 何时需要用到 atan2

在坐标系中理解tan 和 atan

回顾一下三角函数tan：

tanθ，用三角函数来表示时，它的值等于sinθ/cosθ，如果将其放到坐标系中，它的的值等价于：dy/dx。在坐标系中，任意两个点所组成的直线，相对于x轴的斜率就是tanθ = dy /dx，相对于y轴的斜率就是dx/dy ，此时我们用cot来表示；其中，dy 是两个点的y坐标的差值，dx是两个点的x坐标的差值。

那么坐标系内除了y轴，任何一个点(x,y)，相对于x轴的斜率就是y-0/x-0，也即是y/x。

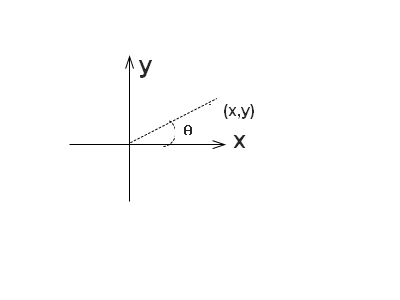
我们将tanθ称为一条直线相对于x轴的斜率，那么θ就是相对于x轴的夹角（旋转角度）了。

tan，是根据角度计算斜率的。那么反过来 arctan（反正切）自然就认为是根据斜率来计算角度的。

为何存在atan2 ?

在JavaScript中，提供了两个arctan函数，一个是atan, 一个是atan2。 atan就是我们所熟知arctan。其实在很多编程语言中都提供了atan2。

那么atan2又是怎么回事呢？

要知道这个，需要知道arctan的不足之处：

arctan的返回值范围是(-π/2, π/2) 不包括， ±π/2，也就是(两个点组成的直线与x轴夹角是90°)90°是计算不出来的。为啥呢?在计算arctan ( dy/dx)时，如果两个点(x1,y1),(x2,y2)组成的直线与x轴的夹角呈90°时，dx= x2-x1 = 0 ，0 是不能作为除数的，所以就无法计算这种情形。

值的范围也就是计算的角度的范围在（-π/2, π/2），从坐标系来看，这个角度的范围只能是在第1、4象限，并不能表示出第2、3象限的角。

为了弥补atan的不足，在计算机编程领域，引入了atan2函数，它的计算结果是在(-π,π]。它正好可以覆盖整个坐标系，包括90°的情形。

它的计算过程是怎样的呢？

关于这个，我从wikipedia上摘取了它的计算过程：

atan2的应用

在第一小节中的那张图中的坐标系，是我们熟知的。在HTML、Canvas中，坐标系并不像我们熟知的坐标系那样。它是这样的：

从x轴正向沿顺时针方向，所经过的角度分别是0，π/2, π，3π/2，2π。

从x轴正向沿逆时针方向，所经过的角度分别是0，-π/2, -π，-3π/2，-2π。

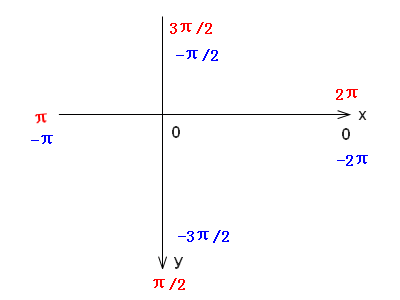
atan2的结果在(-π，π]之间，恰好一周，四个象限全覆盖。从坐标系来看，顺时针方向的值是正值，逆时针方向的值是负的。

从坐标系上来看，atan2结果是（0,-π）时就表示，从x轴正向逆时针方向转最大 π弧度（180角度）。同理，(0,π)表示从x轴正向顺时针转最大π弧度（180角度）。

在第1）小节中说了atan可以用来计算平面坐标系内任意两点的连线与x轴正向之间的夹角。而atan2是atan的补充，那么使用atan2自然就可以来计算平面坐标系内任意两点的连线与x轴正向之间的夹角了。

如果两个点在第一象限内：

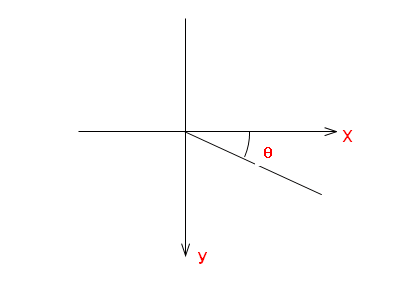
如果两个点在第四象限内：

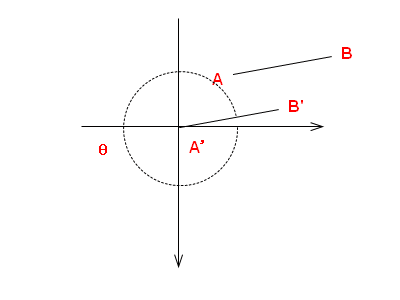
如果两个点在不同的象限内，我们也可以平移来看。

何时需要使用atan2 ?

目前我遇到了两种情况，是通过atan2来解决的：

1）在平面坐标系内任意两个点间画一条带有箭头的直线（可以是单向箭头，可以是双向箭头）。在这个需求中，另外也知道了箭头的一条边与直线的夹角和箭头的长度。

这个需求的难点就是要计算出箭头的另外两个点坐标。

2）在平面坐标系内任意两个点之间画一条指定曲率的曲线（arc）。在这个需求中，要计算arc，自然要知道radius, startAngle, endAngle，圆心坐标。可以根据曲率来计算出半径等，但是难点在计算圆心坐标。

这两个需求的共同特点是：

1）两个已知的点

2）根据这两个点和其他的条件去计算一些必须的（画line,arc等必须的）点坐标。

目前我遇到了这两种需求，都通过atan2来解决的。其他的情况，目前尚且未知，待后续发现时，补充上。