【算法】赫夫曼树(Huffman)的构建和应用(编码、译码)
赫夫曼树的概念
二叉树结点的度
扩充二叉树


赫夫曼树的外结点和内结点
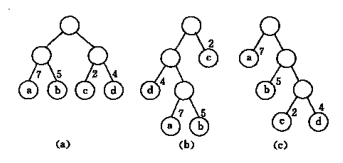
带权路径长度WPL
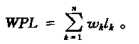

赫夫曼树(最优二叉树)

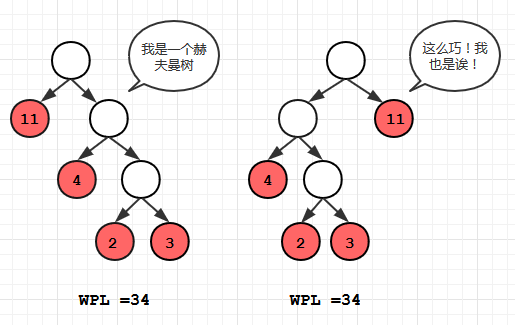

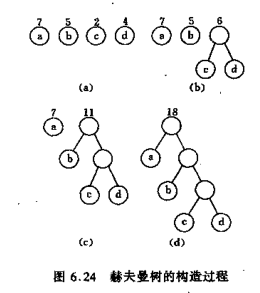
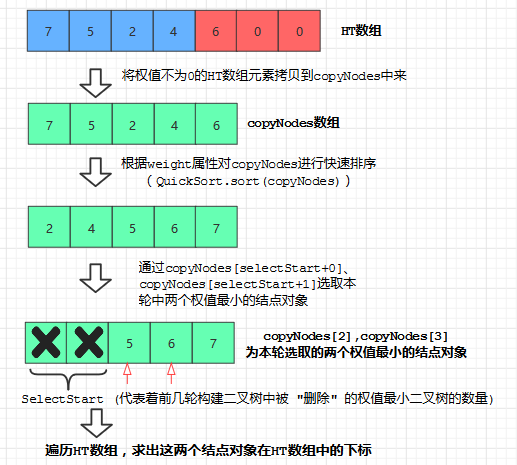
赫夫曼树的构建

Node类的设计
/**
* @Author: HuWan Peng
* @Date Created in 23:21 2018/1/14
*/
public class Node {
char data; // 数据
int weight; // 权值
int left, right, parent; // 三条链接
public Node (char data, int weight) {
this.data = data;
this.weight = weight;
}
public Node (int weight) {
this.weight = weight;
}
}
buildTree方法的设计



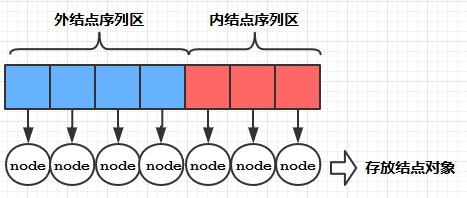
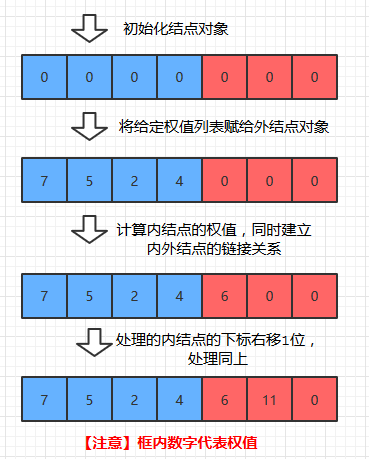

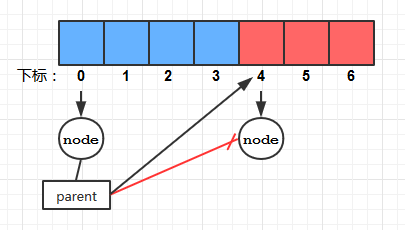

具体代码
/**
* @description: 构建赫夫曼树
*/
public Node[] buildTree (Node [] nodes) {
int s1, s2,p;
int n = nodes.length; // 外结点的数量
int m = 2*n - 1; // 内结点 + 外结点的总数量
Node [] HT = new Node [m]; // 存储结点对象的HT数组
for (int i=0;i<m;i++) HT[i] = new Node(0); // 初始化HT数组元素
for (int i=0;i<n;i++) {
HT[i].data = nodes[i].data;
HT[i].weight = nodes[i].weight; //将给定的权值列表赋给外结点对象
}
for (int i=n;i<m;i++) {
s1 = select(HT,i,0); // 取得HT数组中权值最小的结点对象的下标
s2 = select(HT,i,1); // 取得HT数组中权值次小的结点对象的下标
HT[i].left = s1; // 建立链接
HT[i].right = s2;
HT[s1].parent = i;
HT[s2].parent = i;
HT[i].weight = HT[s1].weight + HT[s2].weight;// 计算当前外结点的权值
selectStart+=2; // 这个变量表示之前“被删除”的最小结点的数量和
}
return HT; // 将处理后的HT数组返回
}
/**
* @description: buildTree方法的用例
*/
public static void main (String [] args) {
Node [] nodes = new Node[4];
nodes[0] = new Node('a',7);
nodes[1] = new Node('b',5);
nodes[2] = new Node('c',2);
nodes[3] = new Node('d',4);
HuffmanTree ht = new HuffmanTree();
Node [] n = ht.buildTree(nodes); // n是构建完毕的赫夫曼树
}
}
select方法的设计
private int select (Node[] HT,int range, int rank)
s1 = select(HT,i,0); // 取得HT数组中权值最小的结点对象的下标
s2 = select(HT,i,1); // 取得HT数组中权值次小的结点对象的下标

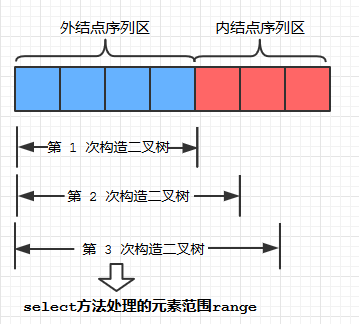
/**
* @description: 返回权值排名为rank的结点对象在HT中的下标(按权值从小到大排)
*/
private int select (Node[] HT,int range, int rank) {
Node [] copyNodes = Arrays.copyOf(HT, range);// 将HT[0]~HT[range]拷贝到copyNodes中
QuickSort.sort(copyNodes); // 对copyNodes进行从小到大的快速排序
Node target = copyNodes[rank + selectStart]; // 取得“删除”后权值排名为rank的结点对象
for (int j=0;j<HT.length;j++) {
if (target == HT[j]) return j; // 返回该结点对象在数组HT中的下标
}
return -1;
}

赫夫曼树的应用
等长编码和不等长编码


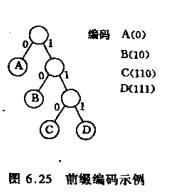
前缀编码
赫夫曼编码的作用



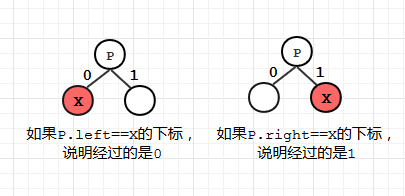
实现赫夫曼编码(encode)


- 如果P.left==X在HT中的下标,则说明X是P的左分支,说明经过的是 0
- 如果P.right==X在HT中的下标,则说明X是P的右分支,说明经过的是 1

import java.util.Arrays;
/**
* @Author: HuWan Peng
* @Date Created in 22:54 2018/1/14
*/
public class HuffmanTree {
private class HuffmanCode {
char data; // 存放字符,例如 'C'
String bit; // 存放编码后的字符串, 例如"111"
public HuffmanCode (char data, String bit) {
this.data = data;
this.bit = bit;
}
}
/**
* @description: 构建赫夫曼树
*/
public Node[] buildTree (Node [] nodes) {
// 具体代码见上文
}
/**
* @description: 进行赫夫曼编码
*/
public HuffmanCode [] encode(Node [] nodes) {
Node [] HT = buildTree(nodes); // 根据输入的nodes数组构造赫夫曼树
int n = nodes.length;
HuffmanCode [] HC = new HuffmanCode [n];
String bit;
for (int i=0;i<n;i++) { // 遍历各个叶子结点
bit = "";
for (int c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent) { // 从叶子结点上溯到根结点
if(HT[f].left == c) bit= "0" + bit; // 反向编码
else bit= "1" + bit;
}
HC[i] = new HuffmanCode(HT[i].data,bit); // 将字符和对应的编码存储起来
}
return HC;
}
/**
* @description: encode方法的用例
*/
public static void main (String [] args) {
Node [] nodes = new Node[4];
nodes[0] = new Node('A',7);
nodes[1] = new Node('B',5);
nodes[2] = new Node('C',2);
nodes[3] = new Node('D',4);
HuffmanTree ht = new HuffmanTree();
HuffmanCode[] hc = ht.encode(nodes);
// 对A,B,C,D进行编码
for (int i=0;i<hc.length;i++) { // 将赫夫曼编码打印出来
System.out.println(hc[i].data + ":" +hc[i].bit);
}
}
}
A:0
B:10
C:110
D:111
赫夫曼译码(decode)
import java.util.Arrays;
/**
* @Author: HuWan Peng
* @Date Created in 22:54 2018/1/14
*/
public class HuffmanTree {
int selectStart = 0;
private class HuffmanCode {
char data; // 存放字符,例如 'C'
String bit; // 存放编码后的字符串, 例如"111"
public HuffmanCode (char data, String bit) {
this.data = data;
this.bit = bit;
}
}
/**
* @description: 构建赫夫曼树
*/
public Node[] buildTree (Node [] nodes) {
// 代码见上文
}
/**
* @description: 进行赫夫曼译码
*/
public String decode (Node [] nodes, String code) {
String str="";
Node [] HT = buildTree(nodes);
int n =HT.length -1;
for (int i=0;i<code.length();i++) {
char c = code.charAt(i);
if(c == '1') {
n = HT[n].right;
}
else {
n = HT[n].left;
}
if(HT[n].left == 0) {
str+= HT[n].data;
n =HT.length -1;
}
}
return str;
}
/**
* @description: decode方法的用例
*/
public static void main (String [] args) {
Node [] nodes = new Node[4];
nodes[0] = new Node('A',7);
nodes[1] = new Node('B',5);
nodes[2] = new Node('C',2);
nodes[3] = new Node('D',4);
HuffmanTree ht = new HuffmanTree();
// 对 010110111 进行译码
System.out.println(ht.decode(nodes,"010110111"));
}
}
ABCD
全部代码:
Node.java
/**
* @Author: HuWan Peng
* @Date Created in 23:21 2018/1/14
*/
public class Node {
char data;
int weight;
int left, right, parent;
public Node (char data, int weight) {
this.data = data;
this.weight = weight;
}
public Node (int weight) {
this.weight = weight;
}
}
HuffmanTree.java
import java.util.Arrays;
/**
* @Author: HuWan Peng
* @Date Created in 22:54 2018/1/14
*/
public class HuffmanTree {
int selectStart = 0;
private class HuffmanCode {
char data; // 存放字符,例如 'C'
String bit; // 存放编码后的字符串, 例如"111"
public HuffmanCode (char data, String bit) {
this.data = data;
this.bit = bit;
}
}
/**
* @description: 返回权值排名为rank的结点对象在nodes中的下标(按权值从小到大排)
*/
private int select (Node[] HT,int range, int rank) {
Node [] copyNodes = Arrays.copyOf(HT, range);// 将HT[0]~HT[range]拷贝到copyNodes中
QuickSort.sort(copyNodes); // 对copyNodes进行从小到大的快速排序
Node target = copyNodes[rank + selectStart]; // 取得“删除”后权值排名为rank的结点对象
for (int j=0;j<HT.length;j++) {
if (target == HT[j]) return j; // 返回该结点对象在数组HT中的下标
}
return -1;
}
/**
* @description: 构建赫夫曼树
*/
public Node[] buildTree (Node [] nodes) {
int s1, s2,p;
int n = nodes.length; // 外结点的数量
int m = 2*n - 1; // 内结点 + 外结点的总数量
Node [] HT = new Node [m]; // 存储结点对象的HT数组
for (int i=0;i<m;i++) HT[i] = new Node(0); // 初始化HT数组元素
for (int i=0;i<n;i++) {
HT[i].data = nodes[i].data;
HT[i].weight = nodes[i].weight; //将给定的权值列表赋给外结点对象
}
for (int i=n;i<m;i++) {
s1 = select(HT,i,0); // 取得HT数组中权值最小的结点对象的下标
s2 = select(HT,i,1); // 取得HT数组中权值次小的结点对象的下标
HT[i].left = s1; // 建立链接
HT[i].right = s2;
HT[s1].parent = i;
HT[s2].parent = i;
HT[i].weight = HT[s1].weight + HT[s2].weight;// 计算当前外结点的权值
selectStart+=2; // 这个变量表示之前“被删除”的最小结点的数量和
}
return HT; // 将处理后的HT数组返回
}
/**
* @description: 进行赫夫曼编码
*/
public HuffmanCode [] encode(Node [] nodes) {
Node [] HT = buildTree(nodes); // 根据输入的nodes数组构造赫夫曼树
int n = nodes.length;
HuffmanCode [] HC = new HuffmanCode [n];
String bit;
for (int i=0;i<n;i++) { // 遍历各个叶子结点
bit = "";
for (int c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent) { // 从叶子结点上溯到根结点
if(HT[f].left == c) bit= "0" + bit; // 反向编码
else bit= "1" + bit;
}
HC[i] = new HuffmanCode(HT[i].data,bit); // 将字符和对应的编码存储起来
}
return HC;
}
/**
* @description: 进行赫夫曼译码
*/
public String decode (Node [] nodes, String code) {
String str="";
Node [] HT = buildTree(nodes);
int n =HT.length -1;
for (int i=0;i<code.length();i++) {
char c = code.charAt(i);
if(c == '1') {
n = HT[n].right;
}
else {
n = HT[n].left;
}
if(HT[n].left == 0) {
str+= HT[n].data;
n =HT.length -1;
}
}
return str;
}
/**
* @description: buildTree方法的用例
*/
public static void main (String [] args) {
Node [] nodes = new Node[4];
nodes[0] = new Node('A',7);
nodes[1] = new Node('B',5);
nodes[2] = new Node('C',2);
nodes[3] = new Node('D',4);
HuffmanTree ht = new HuffmanTree();
System.out.println(ht.decode(nodes,"010110111"));
}
}
QuickSort.java
/**
* @Author: HuWan Peng
* @Date Created in 22:56 2018/1/14
*/
public class QuickSort {
/**
* @description: 交换两个数组元素
*/
private static void exchange(Node [] a , int i, int j) {
Node temp = a[i];
a[i] = a[j];
a[j] = temp;
}
/**
* @description: 切分函数
*/
private static int partition (Node [] a, int low, int high) {
int i = low, j = high+1; // i, j为左右扫描指针
int pivotkey = a[low].weight; // pivotkey 为选取的基准元素(头元素)
while(true) {
while (a[--j].weight>pivotkey) { if(j == low) break; } // 右游标左移
while(a[++i].weight<pivotkey) { if(i == high) break; } // 左游标右移
if(i>=j) break; // 左右游标相遇时候停止, 所以跳出外部while循环
else exchange(a,i, j) ; // 左右游标未相遇时停止, 交换各自所指元素,循环继续
}
exchange(a, low, j); // 基准元素和游标相遇时所指元素交换,为最后一次交换
return j; // 一趟排序完成, 返回基准元素位置
}
/**
* @description: 根据给定的权值对数组进行排序
*/
private static void sort (Node [] a, int low, int high) {
if(high<= low) { return; } // 当high == low, 此时已是单元素子数组,自然有序, 故终止递归
int j = partition(a, low, high); // 调用partition进行切分
sort(a, low, j-1); // 对上一轮排序(切分)时,基准元素左边的子数组进行递归
sort(a, j+1, high); // 对上一轮排序(切分)时,基准元素右边的子数组进行递归
}
public static void sort (Node [] a){ //sort函数重载, 只向外暴露一个数组参数
sort(a, 0, a.length-1);
}
}

【算法】赫夫曼树(Huffman)的构建和应用(编码、译码)的更多相关文章
- Android版数据结构与算法(七):赫夫曼树
版权声明:本文出自汪磊的博客,未经作者允许禁止转载. 近期忙着新版本的开发,此外正在回顾C语言,大部分时间没放在数据结构与算法的整理上,所以更新有点慢了,不过既然写了就肯定尽力将这部分完全整理好分享出 ...
- C#数据结构-赫夫曼树
什么是赫夫曼树? 赫夫曼树(Huffman Tree)是指给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小.哈夫曼树(也称为最优二叉树)是带权路径长度最短的树,权值较大的结点 ...
- Java数据结构和算法(四)赫夫曼树
Java数据结构和算法(四)赫夫曼树 数据结构与算法目录(https://www.cnblogs.com/binarylei/p/10115867.html) 赫夫曼树又称为最优二叉树,赫夫曼树的一个 ...
- 【数据结构】赫夫曼树的实现和模拟压缩(C++)
赫夫曼(Huffman)树,由发明它的人物命名,又称最优树,是一类带权路径最短的二叉树,主要用于数据压缩传输. 赫夫曼树的构造过程相对比较简单,要理解赫夫曼数,要先了解赫夫曼编码. 对一组出现频率不同 ...
- 赫夫曼树JAVA实现及分析
一,介绍 1)构造赫夫曼树的算法是一个贪心算法,贪心的地方在于:总是选取当前频率(权值)最低的两个结点来进行合并,构造新结点. 2)使用最小堆来选取频率最小的节点,有助于提高算法效率,因为要选频率最低 ...
- javascript实现数据结构: 树和二叉树的应用--最优二叉树(赫夫曼树),回溯法与树的遍历--求集合幂集及八皇后问题
赫夫曼树及其应用 赫夫曼(Huffman)树又称最优树,是一类带权路径长度最短的树,有着广泛的应用. 最优二叉树(Huffman树) 1 基本概念 ① 结点路径:从树中一个结点到另一个结点的之间的分支 ...
- puk1521 赫夫曼树编码
Description An entropy encoder is a data encoding method that achieves lossless data compression by ...
- Python---哈夫曼树---Huffman Tree
今天要讲的是天才哈夫曼的哈夫曼编码,这是树形数据结构的一个典型应用. !!!敲黑板!!!哈夫曼树的构建以及编码方式将是我们的学习重点. 老方式,代码+解释,手把手教你Python完成哈夫曼编码的全过程 ...
- 哈夫曼树Huffman
哈夫曼树处理这样的一种问题: 给出一棵n个叶子的k叉树,每个叶子有一个权值wi,要求最小化∑wi*di di表示,第i个叶子节点到根节点的距离.(一般是边数) 处理方法比较固定. 贪心的思路:我们让权 ...
随机推荐
- 查询linux版本命令
[环境] Ubuntu [本文命令记录] uname -a lsb_release cat /etc/issue cat /proc/version [截图效果] (1)uname -a (2)lsb ...
- [100个改变摄影的伟大观念].(英)玛瑞恩.高清扫描版.pdf
下载地址 :https://u253469.ctfile.com/fs/253469-229765365
- Vagrant安装完lnmp后,配置linux和windows共享文件并配置虚拟主机访问项目
虚拟机目录下的Vagrantfile文件是vagrant的配置文件,如果想把虚拟机当作一台服务器,可以通过ip访问,需要修改配置文件进行配置. (1)第一步:打开虚拟机目录下的Vagrantfile文 ...
- ABP-Module
[TOC] 什么是Module? Module就是模块化的设计思想.开发人员可以将自定义的功能以模块的形式集成到项目中.具体的功能也可以设计成一个单独的模块 AbpModule AbpModule是所 ...
- 基于Vue的SPA动态修改页面title的方法
最近基于VUE做个SPA手机端web发现动态修改页面标题通过document.title=xxxx 来修改着实蛋疼,而且在IOS的微信端据说没效果.百度发现要针对IOS的微信做点额外的操作,即:创建一 ...
- [置顶]
bootstrap自定义样式-bootstrap侧边导航栏的实现
前言 bootstrap自带的响应式导航栏是向下滑动的,有时满足不了个性化的需求,需要做一个类似于android drawerLayout 侧滑的菜单,这就是我要实现的bootstrap自定义侧滑菜单 ...
- Java 浮点型与双精度数值比较
对于双精度与浮点数之间的比较存在潜在的转化
- eclipse 更换 JDK 版本后报错
在实际开发过程中,可能由于项目的需要,我们需要更换 JDK 的版本.但是更换后会报错,如下: Java compiler level does not match the version of the ...
- elastaticresearch 学习过程
1.在Windows上安装了es 2.在chrome上装了sense 3.尝试创建 es 的模板
- php curl 请求302跳转页面
今天对接支付接口,需要获取支付页面,发现支付商那边给的链接会发送302 跳转,最后发现该方法,绝对给力: <?php $url = 'http://auto.jrj.com.cn/'; $ch ...
