二叉树（Java实现）

一、常见用语

1、逻辑结构：描述数据之间逻辑上的相关关系。分为线性结构（如，字符串），和非线性结构（如，树，图）。

2、物理结构：描述数据的存储结构，分为顺序结构（如，数组）和链式结构。

3、结点的度：一个节点子树（即分支）个数。

4、叶结点：也称为终端节点，指度为0的节点。

5、树的深度（高度）：树中结点层次的最大值。

6、有序树：子树有先后次序之分（我的理解就是左右节点次序不可以颠倒）。

7、同构：将节点适当重命名，即可得两颗完全相同的树

8、孩子节点：一个节点的直接后继节点。

9、双亲节点：一个节点的直接前驱节点。

二、二叉树中的概念

1、二叉树：满足以下两个条件的树称为二叉树

①节点的度不可以超过2

②节点的孩子节点次序不可颠倒

2、满二叉树：每层得节点数都是满的，即2^i-1

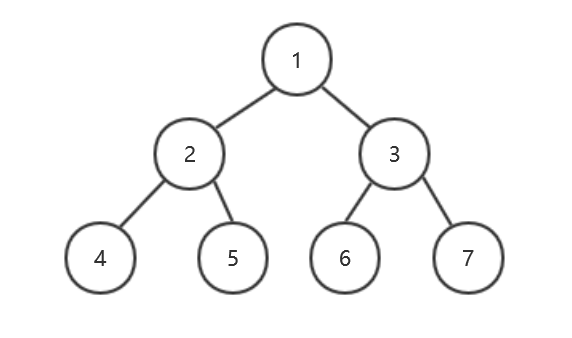
3、完全二叉树：节点1~n分别对应于满二叉树的节点1~n

4、完全二叉树的性质：

（1）若节点序号为i（i>1），则其双亲节点序号为i/2。（这里是整除）

（2）若节点序号为i（i>=1），则其左子节点序号为2i。

（3）若节点序号为i （i>=1），则其右子节点序号为2i+1。

三、二叉树的操作

 1、二叉树节点的存储结构

public class TreeNode {
    String data;
    TreeNode LChild;
    TreeNode RChild;
    TreeNode(String data) {
        this.data = data;
    }
    public String toString() {
        return data;
    }
}

 2、创建二叉树

使用前序遍历创建二叉树是比较合适，按照逻辑，总要先创建根节点在创建左右子树，总不能还没有创建根节点就把root.LChild传递出去吧。

private static String[] tree = {"A","B",".",".","C","D",".",".","."};
private static int i = 0;
//先序创建二叉树是比较合适的
TreeNode inOrderCreateBTree() {
    TreeNode bt = null;
    String s = tree[i++];
    if(s == ".") {
        return bt;
    }else {
        bt = new TreeNode(s);
        bt.LChild = inOrderCreateBTree();
        bt.RChild = inOrderCreateBTree();
        return bt;
    }
}

可以用非递归的方式建树，但是难度还是挺大的。

3、先序遍历

递归方式：

//递归法前序遍历二叉树
void preOrderPrintBTree(TreeNode bt) {
    if(bt == null) {
        System.out.print("." + " ");
    }else {
        System.out.print(bt + " ");
        preOrderPrintBTree(bt.LChild);
        preOrderPrintBTree(bt.RChild);
    }
}

基于栈的非递归方式：

跟着思路写就好：事实上这就是一个代码的模板，三种遍历的代码在结构上都是差不多的。

①指针移到最左子孙节点，边移变打印，边入栈（入栈是为了保存双亲节点，以便访问右子树）。

while(p != null) {
    System.out.print(p + " ");
    stack.push(p);
    p = p.LChild;
    if(p == null) {
        System.out.print("." + " ");
    }
}

②栈不空，就出栈，p指针指向右子树。

if(!stack.isEmpty()) {
    p = stack.pop();
    p = p.RChild;
    if(p == null) {
        System.out.print("." + " ");
    }
}

完整代码：

//基于栈的非递归法先序遍历二叉树
void preOrderPrintBTree1(TreeNode bt) {
    if(bt == null) {
        System.out.println("null tree");
    }
    Stack<TreeNode> stack = new Stack<TreeNode>();
    TreeNode p = bt;
    while(!stack.isEmpty() || p != null) {
        while(p != null) {
            System.out.print(p + " ");
            stack.push(p);
            p = p.LChild;
            if(p == null) {
                System.out.print("." + " ");
            }
        }
        if(!stack.isEmpty()) {
            p = stack.pop();
            p = p.RChild;
            if(p == null) {
                System.out.print("." + " ");
            }
        }
    }
}

 4、中序遍历

递归法：

void inOrderPrint(TreeNode bt) {
    if(bt == null) {
        System.out.print("." + " ");
    } else {
        inOrderPrint(bt.LChild);
        System.out.print(bt + " ");
        inOrderPrint(bt.RChild);
    }
}

非递归法：

前序遍历和中序遍历是查不多的，前者先打印后入栈，后者是先入栈后打印。

①p指针移到最左端，边移变入栈。

while(p != null) {
    stack.push(p);
    p = p.LChild;
}

②边出栈边打印，p指针指向右子树

if(!stack.isEmpty()) {
    p = stack.pop();
    System.out.print(p + " ");
}

完整代码：

void inOrderPrint1(TreeNode bt) {
    if(bt == null) {
        System.out.println(".");
    }else {
        Stack<TreeNode> stack = new Stack<TreeNode>();
        TreeNode p = bt;
        while(!stack.isEmpty() || p != null) {
            while(p != null) {
                stack.push(p);
                p = p.LChild;
            }
            if(!stack.isEmpty()) {
                p = stack.pop();
                System.out.print(p + " ");
            }
        }
    }
}

 5、后续遍历

递归：

void postOrderPrint(TreeNode bt) {
    if(bt == null) {
        System.out.print("." + " ");
    }else {
        postOrderPrint(bt.LChild);
        postOrderPrint(bt.RChild);
        System.out.print(bt + " ");
    }
}

非递归：后续遍历的难点就在于要知道前一次访问的节点是左孩子还是右孩子，所以要设置一个前置指针pre。

①pcur指针移到最左端，边移边入栈

②pcur的有孩子被为null或者被访问过，则访问pcur，否则pcur要继续入栈，pcur指向其右孩子。

完整代码：

void postOrderPrint1(TreeNode bt) {
    if(bt == null) {
        System.out.print("." + " ");
    }else {
        Stack<TreeNode> stack = new Stack<TreeNode>();
        TreeNode pcur = bt;
        TreeNode pre = null;
        while(pcur != null) {
            stack.push(pcur);
            pcur = pcur.LChild;
        }
        while(!stack.isEmpty()) {
            pcur = stack.pop();

            if(pcur.RChild == null || pcur.RChild == pre) {
                System.out.print(pcur + " ");
                pre = pcur;
            }else {
                stack.push(pcur);
                pcur = pcur.RChild;
                while(pcur != null) {
                    stack.push(pcur);
                    pcur = pcur.LChild;
                }
            }
        }
    }
}

 6、二叉树的其他操作

（1）打印叶子节点

//前序遍历打印叶子节点
public static void preprintLeaves(TreeNode bt) {
    if(bt == null) {

    }else {
        if(bt.LChild == null && bt.RChild == null) {
            System.out.print(bt + " ");
        }
        preprintLeaves(bt.LChild);
        preprintLeaves(bt.RChild);
    }
}

（2）求树的深度

//先序遍历求二叉树的深度
public static int preTreeDepth(TreeNode bt, int h) {
    if(bt != null) {
        if(h > depth) depth = h;
        preTreeDepth(bt.LChild,h+1);
        preTreeDepth(bt.RChild,h+1);
    }
    return depth;
}
//后续遍历求二叉树深度
public static int postTreeDepth(TreeNode bt) {
    int hl = 0;
    int hr = 0;
    int max = 0;
    if(bt == null) {
        return 0;
    }else {
        hl = postTreeDepth(bt.LChild);
        hr = postTreeDepth(bt.RChild);
        max = Math.max(hr, hl);
        return max + 1;
    }
}