数据结构 -- 二叉树（Binary Search Tree）

一、简介

　　在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

　　一棵深度为k，且有2^k-1个结点的二叉树，称为满二叉树。这种树的特点是每一层上的结点数都是最大结点数。而在一棵二叉树中，除最后一层外，若其余层都是满的，并且或者最后一层是满的，或者是在右边缺少连续若干结点，则此二叉树为完全二叉树。具有n个结点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树，至少有（2的k-1次方）个叶子结点，至多有2^k-1个结点。

　　节点特性：1. 每个节点的值都大于其左子树的所有节点的值。

　　　　　　    2. 每个节点的值都小于其右子树的所有节点的值。

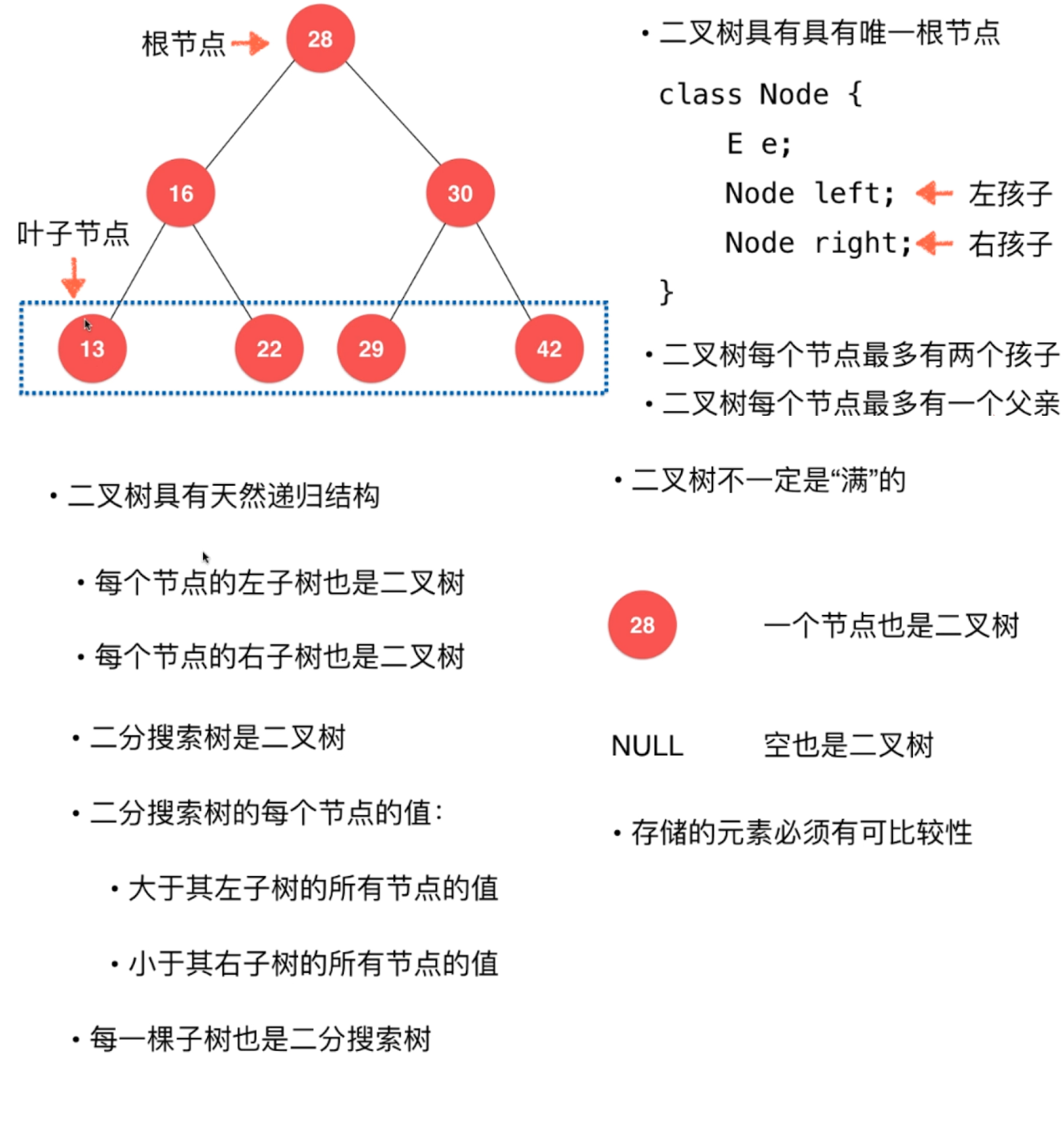
二、代码

　　1.定义一个支持泛型的节点类, 用于存储二分搜索树每个节点的信息, 这个类作为二分搜索树的一个内部类, 二分搜索树的类声明以及Node节点类

public class BinaryTree<E extends Comparable<E>> {
    // 根节点
    private Node root ;
    // 树容量
    private int size ;
    public BSTree() {
        this.root = null ;
        this.size = 0 ;
    }
    public boolean isEmpty() {
        return size == 0 ;
    }
    public int getSize(){
        return size;
    }
    // 二分搜索树节点类
    private class Node {
        public E e ;
        // 左右子树
        public Node left , right ;
        public Node(E e) {
            this.e = e ;
            this.left = null ;
            this.right = null ;
        }
    }
}

　　2. 添加操作：二分搜索树本身的递归特性, 可以很方便的使用递归实现向二分搜索树中添加元素。

    //添加元素
    public void add(E e){
        root = add(root, e);
    }
    //插入元素，递归算法。 返回插入新节点后二叉树的根
    private Node add(Node node, E e){
        //如果当前根节点为空，则直接创建该节点为根节点
        if(node == null){
            size ++;
            return new Node(e);
        }
        if(e.compareTo(node.e) < 0){ //添加元素e 小于 节点元素e，则从左边添加
            node.left = add(node.left,e);
        }else if (e.compareTo(node.e) > 0){ //添加元素e 大于 节点元素e，则从右边添加
            node.right = add(node.right,e);
        }
        return node;
    }

　　3. 查找操作：二分搜索树没有下标, 针对二分搜索树的查找, 定义一个contains方法, 是否包含某个元素, 返回布尔型变量, 这个操作是递归的过程。

 //查询是否包含e元素
    public boolean contains(E e){
        return contains(root, e);
    }
    // 看以node为根的二分搜索树中是否包含元素e, 递归算法
    private boolean contains(Node node, E e){
        if (node == null){
            return false;
        }
        if (node == e){
            return true;
        }else if (e.compareTo(node.e) > 0){ //如果大于根节点元素，则向右子树递归遍历
            return contains(node.right, e);
        }else{ //如果小于根节点元素，则向左子树递归遍历
            return contains(node.left, e);
        }
    }

　　//找出二叉树的最小元素
　　public E minimum(){
   　　 if (size == 0){
        　　throw new IllegalArgumentException("BinaryTree is empty!");
    　　}
    　　return minimum(root).e;
　　}
　　private Node minimum(Node node){
    　　if ( node.left == null){
        　　return node;
    　　}
    　　return minimum(node.left);
　　}
　　//找出二叉树的最大元素
　　public E maximum(){
    　　if (size == 0){
      　　  throw new IllegalArgumentException("BinaryTree is empty!");
    　　}
    　　return maximum(root).e;
　　}
　　private Node maximum(Node node){
   　　 if ( node.right == null){
       　　 return node;
    　　}
    　　return maximum(node.right);
　　}

　　4. 遍历操作

遍历分类：

深度优先遍历 : 1. 前序遍历 : 对当前节点的遍历在对左右孩子节点的遍历之前, 遍历顺序 : 当前节点->左孩子->右孩子 2. 中序遍历 : 对当前节点的遍历在对左右孩子节点的遍历中间, 遍历顺序 : 左孩子->当前节点->右孩子 3. 后序遍历 : 对当前节点的遍历在对左右孩子节点的遍历之后, 遍历顺序 : 左孩子->右孩子->当前节点 广度优先遍历 : 1. 层序遍历 : 按层从左到右进行遍历

前序遍历：最常用/自然的遍历方式：

（一）、递归写法　　

//二叉树的前序遍历
    public void preOrder(){
        preOrder(root);
    }
    // 前序遍历以node为根的二分搜索树, 递归算法
    private void preOrder(Node node){
        if (node == null){
            return;
        }
        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

（二）、非递归写法：通过栈实现二叉树遍历　

// 二分搜索树的非递归前序遍历
public void preOrderNR(){
    Stack<Node> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()){
        Node node = stack.pop();
        System.out.println(node.e);

        if(node.right != null){
            stack.push(node.right);
        }
        if(node.left != null) {
            stack.push(node.left);
        }
    }
}

中序遍历：

//二叉树的中序遍历
    public void inOrder(){
        inOrder(root);
    }
    // 中序遍历以node为根的二分搜索树, 递归算法
    private void inOrder(Node node){
        if (node == null){
            return;
        }
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

后序遍历：

//二叉树的后序遍历
    public void postOrder(){
        postOrder(root);
    }
    // 中序遍历以node为根的二分搜索树, 递归算法
    private void postOrder(Node node){
        if (node == null){
            return;
        }
        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }

层序遍历：

//二叉树的层序遍历
    public void levelOrder(){
        Queue<Node> queue = new LinkedList<>();
        queue.add(root); //先将最上层的根节点加入队列中
        while (!queue.isEmpty()){
            Node node = queue.remove(); //删除队列中的最低端的元素
            System.out.println(node.e); //打印输出

            //输出根节点后，将对应的左/右子树的元素添加到队列中。 队列是先进先出，所以先放左子树再放右子树
            if (node.left != null){
                queue.add(node.left);
            }
            if (node.right != null){
                queue.add(node.right);
            }
        }
    }

前,中,后序遍历总结
　　可以认为在遍历的时候每个节点要访问三次, 对当前节点进行遍历操作时一次, 访问当前节点左子树时一次, 访问当前节点右子树时一次, 可以认为前序遍历就是在第一次访问当前节点时进行操作, 以方便我们理解遍历结果, 下面几张图演示前中后序遍历的访问顺序, 蓝色的点表示在这次访问时对当前节点进行遍历操作

前序递归遍历示意图:　蓝点便是绿色道路经过时，输出当前节点内容　　　　　　　　　　　　　　　　　　　　　　　　　　　　

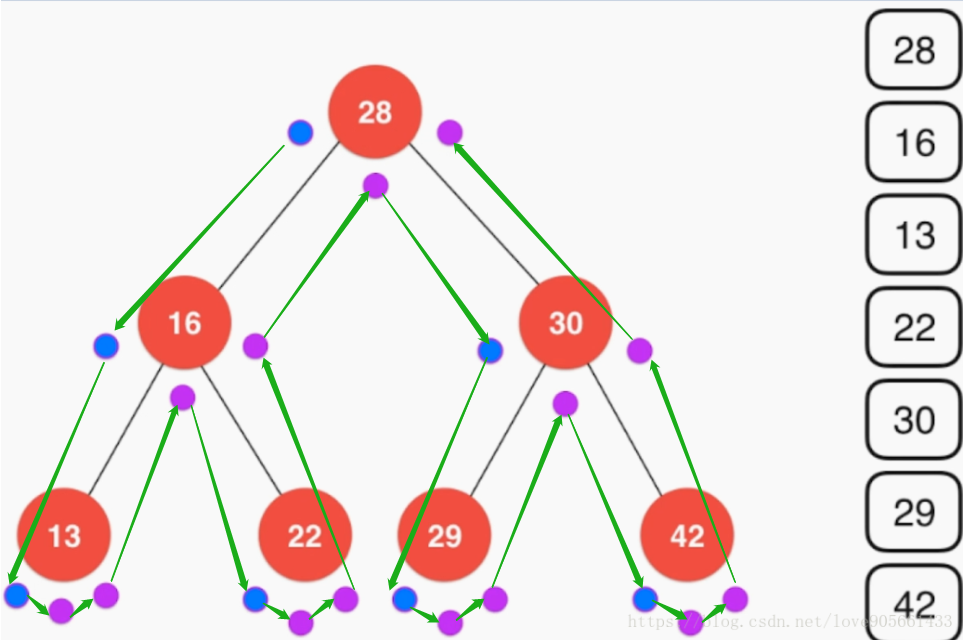
中序递归遍历示意图：同理蓝色为输出点，路径如前序

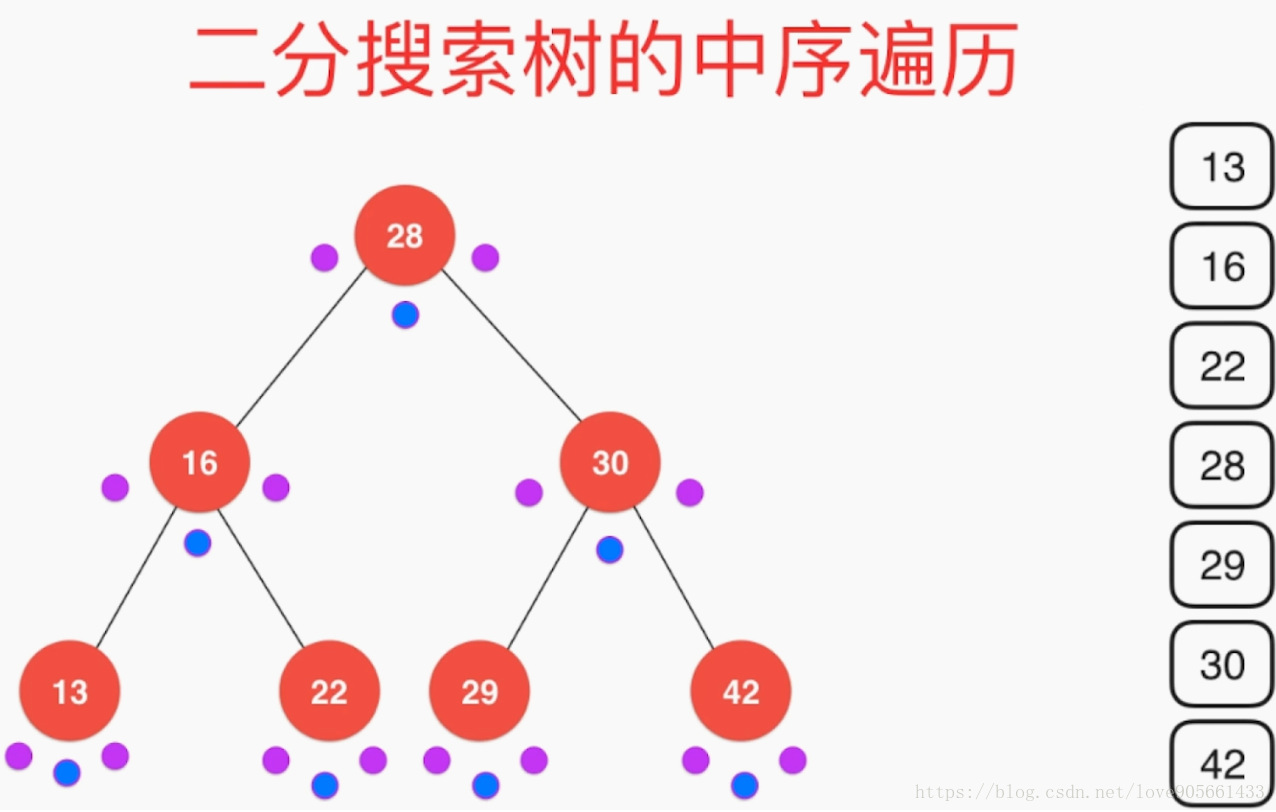
后续递归遍历示意图：同理蓝色为输出点，路径如前序

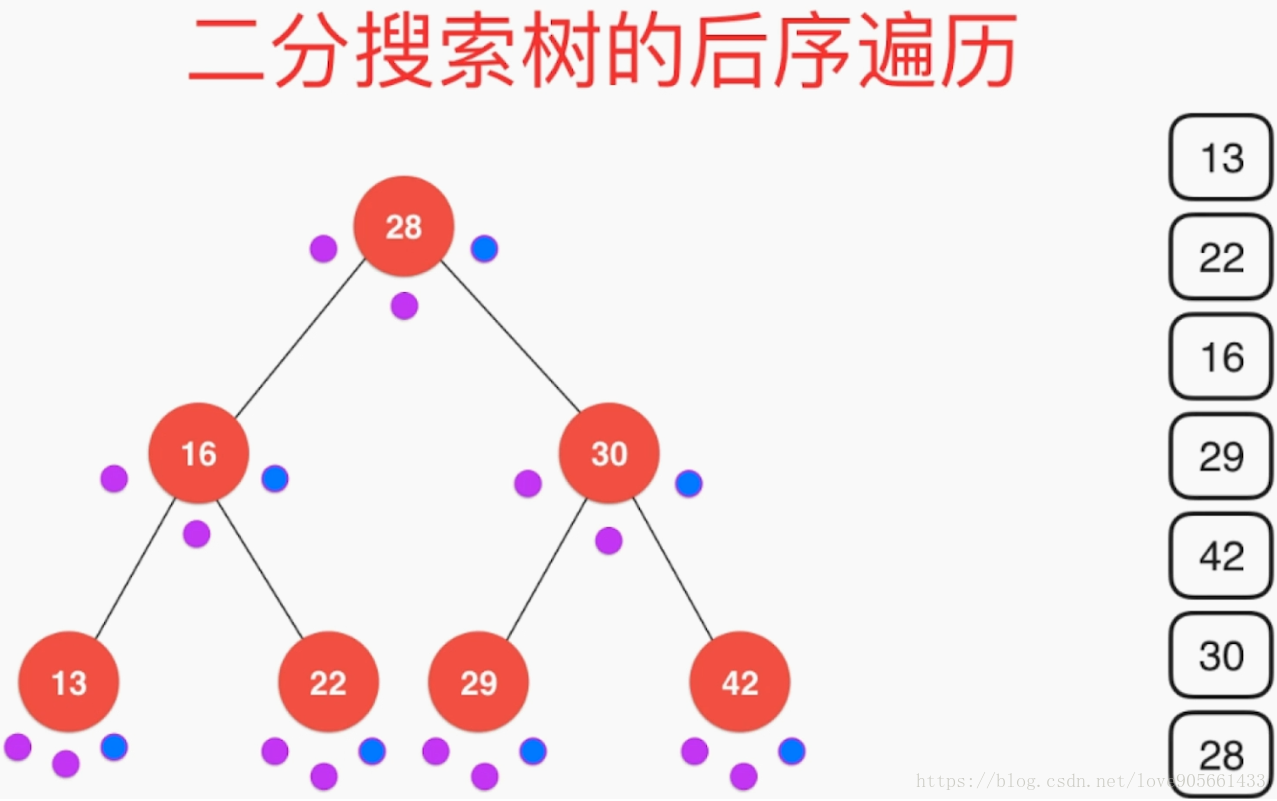
 前序非递归遍历图示：

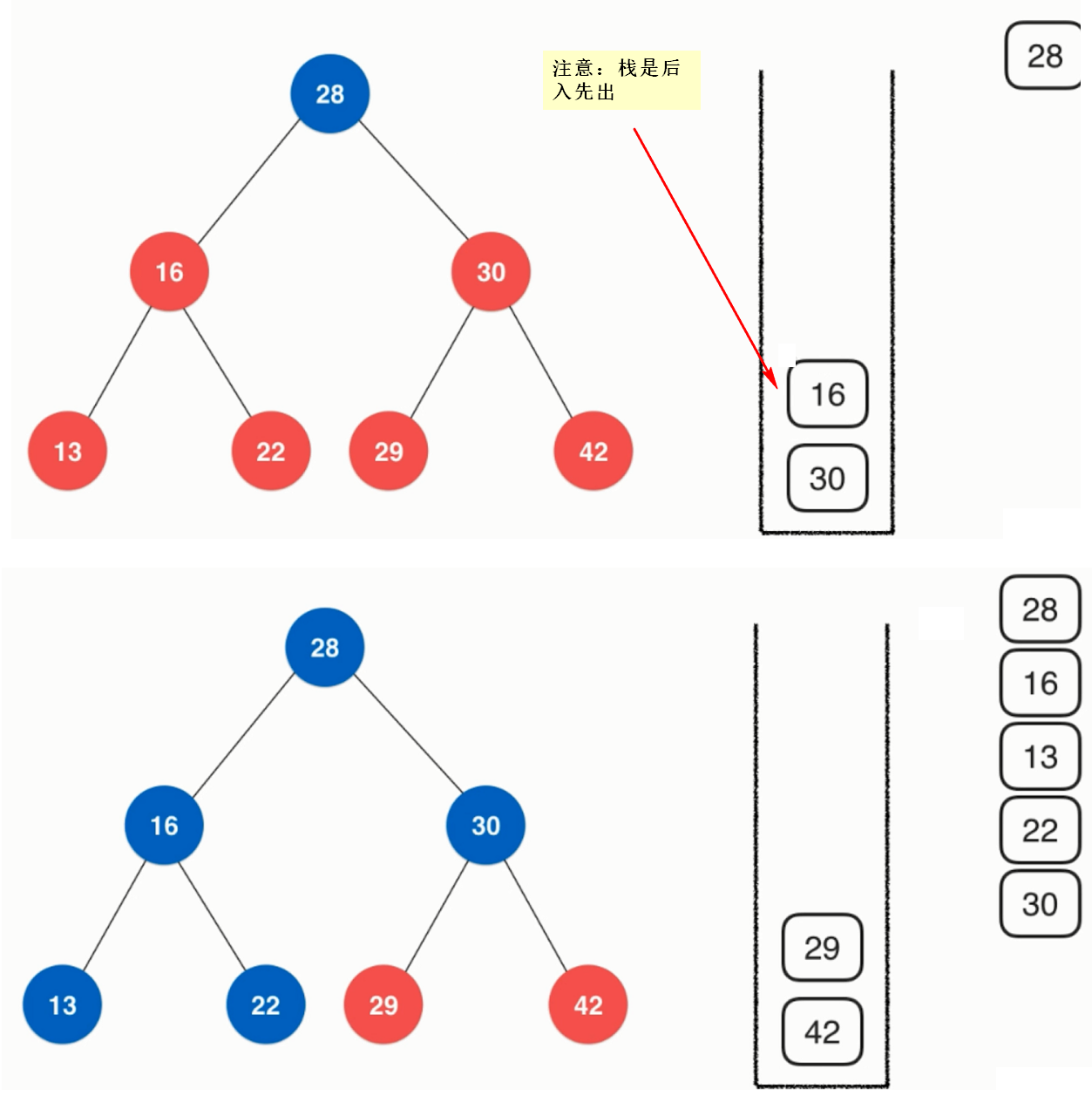
层序遍历示例图：

　　5. 删除操作

（1）删除最大最小节点：

　　删除最小值：找到左子树的最左节点（最小值节点，node.left == null），然后让其上一个节点的左节点指向当前最小值节点的右子树，同时删除最小值节点（node.right = null）；

　　删除最大值：找到右子树的最右节点（最大值节点，node.right == null），然后让其上一个节点的右节点指向当前最大值节点的左子树，同时删除最大值节点（node.left = null）。

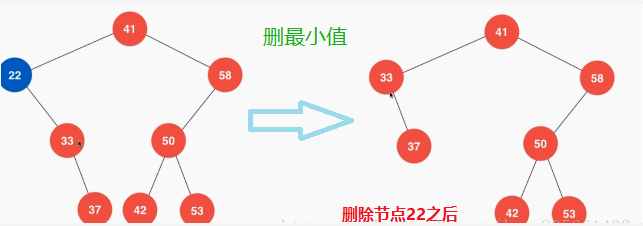
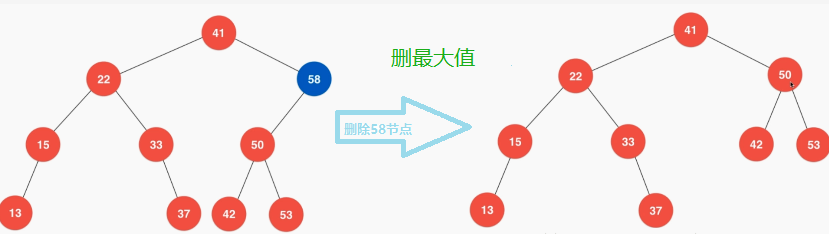
删除最小值代码：

 // 从二分搜索树中删除最小值所在节点, 返回最小值
    public E removeMin(){
        E ret = minimum(); //查找二叉树的最小值
        root = removeMin(root);
        return ret;
    }
    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMin(Node node){
    　　 //当递归循环到node.left节点为空时，即当前node节点便是要删除的最小元素，将其与二叉树分离
        if (node.left == null){
            Node rightNode = node.right;
            node.right = null;//与二叉树脱离
            size --; //数量减一
            return rightNode;
        }
        node.left = removeMin(node.left);
        return node;
    }

删除最大值代码：

// 从二分搜索树中删除最大值所在节点
    public EremoveMax(){
        E ret = maximum(); //查找二叉树的最大值
        root = removeMax(root);
        return ret;
    }
    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMax(Node node) {
        if (node.right == null){
            Node leftNode = node.left;
            node.left = null;//与二叉树脱离
            size --;
            return leftNode;
        }
        node.right = removeMax(node.right);
        return node;
    }

（2）删除任意节点元素

　　删除任意节点可以分为以下几种情况 :

　　　　* 删除叶子节点, 直接删除即可

　　　　* 删除只有右子树的节点, 逻辑同删除最小值, 虽然这个节点不一定是最小值, 但是删除逻辑是一样的

　　　　* 删除只有左子树的节点, 逻辑同删除最大值

　　　　* 删除同时具有左右子树的节点, 此时删除节点的步骤稍微复杂一些

* 首先找到要删除的节点
* 然后找到对应节点的前驱或者后继节点, 前驱就是指当前节点的左子树中最大的元素节点, 后继就是指当前节点右子树中最小的元素节点, 下图就是基于后继节点的删除演示
* 使用后继节点替换当前节点, 然后再删除要删除的节点

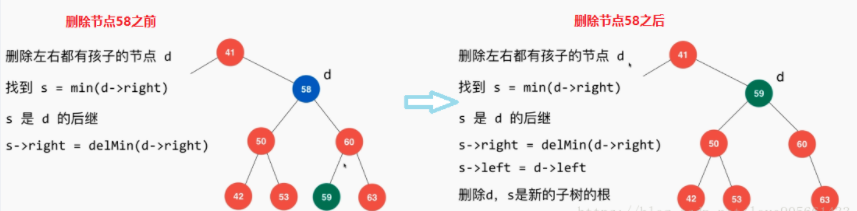
删除任意节点代码：

// 从二分搜索树中删除元素为e的节点
    public void remove(E e){
        root = remove(root, e);
    }
    // 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
    // 返回删除节点后新的二分搜索树的根
    private Node remove(Node node, E e){
        if ( node == null){
            return null;
        }
        if (e.compareTo(node.e) < 0){
            node.left = remove(node.left, e);
            return node;
        }else if(e.compareTo(node.e) > 0){
            node.right = remove(node.right, e);
            return node;
        }else{ //  e.compareTo(node.e) == 0 即找到当前元素

            // 待删除节点左子树为空的情况
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size --;
                return rightNode;
            }
            // 待删除节点右子树为空的情况
            if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size --;
                return leftNode;
            }

            // 待删除节点左右子树均不为空的情况
            // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
            // 用这个节点顶替待删除节点的位置
            Node successor = minimum(node.right);
            successor.right = removeMin(node.right);
            successor.left = node.left;
            node.left = node.right = null;

            return successor;
        }
    }

全部代码：

 package com.wj.BinaryTree;

 import java.util.LinkedList;
 import java.util.Queue;
 import java.util.Stack;

 /**
  * 实现二叉树
  */
 public class BinaryTree<E extends Comparable> {

     private class Node{
         public E e;
         public Node left, right;
         public Node(E e){
             this.e = e;
             left = null;
             right = null;
         }
     }
     private Node root;
     private int size;

     public BinaryTree(){
         root = null;
         size = 0;
     }
     public int size(){
         return size;
     }
     public boolean isEmpty(){
         return size == 0;
     }

     //二叉树的增操作

     //添加元素
     public void add(E e){
         root = add(root, e);
     }
     //插入元素，递归算法。 返回插入新节点后二叉树的根
     private Node add(Node node, E e){
         //如果当前根节点为空，则直接创建该节点为根节点
         if(node == null){
             size ++;
             return new Node(e);
         }
         if(e.compareTo(node.e) < 0){
             node.left = add(node.left,e);
         }else if (e.compareTo(node.e) > 0){
             node.right = add(node.right,e);
         }
         return node;
     }

     //二叉树的查询操作

     //二叉树的前序遍历
     public void preOrder(){
         preOrder(root);
     }
     // 前序遍历以node为根的二分搜索树, 递归算法
     private void preOrder(Node node){
         if (node == null){
             return;
         }
         System.out.println(node.e);
         preOrder(node.left);
         preOrder(node.right);
     }
     // 二分搜索树的非递归前序遍历
     public void preOrderNR(){
         Stack<Node> stack = new Stack<>();
         stack.push(root);
         while (stack !=null){
             Node node = stack.pop();
             System.out.println(node.e);

             if(node.right != null){
                 stack.push(node.right);
             }
             if(node.left != null) {
                 stack.push(node.left);
             }
         }
     }

     //二叉树的中序遍历
     public void inOrder(){
         inOrder(root);
     }
     // 中序遍历以node为根的二分搜索树, 递归算法
     private void inOrder(Node node){
         if (node == null){
             return;
         }
         inOrder(node.left);
         System.out.println(node.e);
         inOrder(node.right);
     }
     //二叉树的后序遍历
     public void postOrder(){
         postOrder(root);
     }
     // 中序遍历以node为根的二分搜索树, 递归算法
     private void postOrder(Node node){
         if (node == null){
             return;
         }
         postOrder(node.left);
         postOrder(node.right);
         System.out.println(node.e);
     }

     //二叉树的层序遍历
     public void levelOrder(){
         Queue<Node> queue = new LinkedList<>();
         queue.add(root); //先将最上层的根节点加入队列中
         while (!queue.isEmpty()){
             Node node = queue.remove(); //删除队列中的最低端的元素
             System.out.println(node.e); //打印输出

             //输出根节点后，将对应的左/右子树的元素添加到队列中
             if (node.left != null){
                 queue.add(node.left);
             }
             if (node.right != null){
                 queue.add(node.right);
             }
         }
     }

     //查询是否包含e元素
     public boolean contains(E e){
         return contains(root, e);
     }
     // 看以node为根的二分搜索树中是否包含元素e, 递归算法
     private boolean contains(Node node, E e){
         if (node == null){
             return false;
         }
         if (node == e){
             return true;
         }else if (e.compareTo(node.e) > 0){ //如果大于根节点元素，则向右子树递归遍历
             return contains(node.right, e);
         }else{ //如果小于根节点元素，则向左子树递归遍历
             return contains(node.left, e);
         }
     }
     //找出二叉树的最小元素
     public Node minimum(){
         if (size == 0){
             throw new IllegalArgumentException("BinaryTree is empty!");
         }
         return minimum(root);
     }
     private Node minimum(Node node){
         if ( node.left == null){
             return node;
         }
         return minimum(node.left);
     }
     //找出二叉树的最大元素
     public Node maximum(){
         if (size == 0){
             throw new IllegalArgumentException("BinaryTree is empty!");
         }
         return maximum(root);
     }
     private Node maximum(Node node){
         if ( node.right == null){
             return node;
         }
         return maximum(node.right);
     }

     // 从二分搜索树中删除最小值所在节点, 返回最小值
     public Node removeMin(){
         Node ret = minimum();
         root = removeMin(root);
         return ret;
     }
     // 删除掉以node为根的二分搜索树中的最小节点
     // 返回删除节点后新的二分搜索树的根
     private Node removeMin(Node node){
         if (node.left == null){
             Node rightNode = node.right;
             node.right = null;
             size --;
             return rightNode;
         }
         node.left = removeMin(node.left);
         return node;
     }
     // 从二分搜索树中删除最大值所在节点
     public Node removeMax(){
         Node ret = maximum();
         root = removeMax(root);
         return ret;
     }
     // 删除掉以node为根的二分搜索树中的最大节点
     // 返回删除节点后新的二分搜索树的根
     private Node removeMax(Node node) {
         if (node.right == null){
             Node leftNode = node.left;
             node.left = null;
             size --;
             return leftNode;
         }
         node.right = removeMin(node.right);
         return node;
     }

     // 从二分搜索树中删除元素为e的节点
     public void remove(E e){
         root = remove(root, e);
     }
     // 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
     // 返回删除节点后新的二分搜索树的根
     private Node remove(Node node, E e){
         if ( node == null){
             return null;
         }
         if (e.compareTo(node.e) < 0){
             node.left = remove(node.left, e);
             return node;
         }else if(e.compareTo(node.e) > 0){
             node.right = remove(node.right, e);
             return node;
         }else{ //  e.compareTo(node.e) == 0 即找到当前元素

             // 待删除节点左子树为空的情况
             if(node.left == null){
                 Node rightNode = node.right;
                 node.right = null;
                 size --;
                 return rightNode;
             }
             // 待删除节点右子树为空的情况
             if(node.right == null){
                 Node leftNode = node.left;
                 node.left = null;
                 size --;
                 return leftNode;
             }

             // 待删除节点左右子树均不为空的情况
             // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
             // 用这个节点顶替待删除节点的位置
             Node successor = minimum(node.right);
             successor.right = removeMin(node.right);
             successor.left = node.left;
             node.left = node.right = null;

             return successor;
         }
     }
     @Override
     public String toString() {
         StringBuilder res = new StringBuilder();
         generateBSTString(root,0,res);
         return res.toString();
     }

     private void generateBSTString(Node node, int depth, StringBuilder res){
         if (node == null){
             res.append(generateDepthString(depth) + "null\n");
             return;
         }
         res.append(generateDepthString(depth) + node.e + "\n");
         generateBSTString(node.left,depth + 1,res);
         generateBSTString(node.right,depth + 1,res);
     }

     private String generateDepthString(int depth){
         StringBuilder res = new StringBuilder();
         for (int i=0; i< depth; i++){
             res.append("--");
         }
         return res.toString();
     }
 }

测试类：

package com.wj.BinaryTree;

import java.util.Objects;

public class Main {
    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();
        int[] nums = {80,50,90,30,60,65,70,100,68,75,101,20,25};
        for (int i : nums){
            binaryTree.add(i);
        }
        System.out.println("=====增后的二叉树=====");
        System.out.println(binaryTree.toString());

        System.out.println("=====二叉树的前序遍历=====");
        // 二叉树的前序遍历
        binaryTree.preOrder();

        System.out.println("=====二叉树的非递归前序遍历=====");
        //二叉树的非递归前序遍历
        binaryTree.preOrderNR();

        System.out.println("=====二叉树的中序遍历=====");
        //二叉树的中序遍历
        binaryTree.inOrder();

        System.out.println("=====二叉树的后序遍历=====");
        //二叉树的后序遍历
        binaryTree.postOrder();

        System.out.println("二叉树的最小节点值："+binaryTree.minimum());
        System.out.println("二叉树的最大节点值："+binaryTree.maximum());
        System.out.println("20是否存在二叉树中："+binaryTree.contains(20));
        System.out.println("200是否存在二叉树中："+binaryTree.contains(200));

        System.out.println("=====删除操作=====");

        Object removeMin = binaryTree.removeMin();
        System.out.println("删除最小的值："+removeMin);
        System.out.println(removeMin+"是否存在二叉树中："+binaryTree.contains((Comparable) removeMin));

        Object removeMax = binaryTree.removeMax();
        System.out.println("删除最大的值："+removeMax);
        System.out.println(removeMax+"是否存在二叉树中："+binaryTree.contains((Comparable) removeMax));

        binaryTree.remove(100);
        System.out.println("100是否存在二叉树中："+binaryTree.contains(100));
    }
}

测试结果：

=====增后的二叉树=====
80
--50
----30
------20
--------null
--------25
----------null
----------null
------null
----60
------null
------65
--------null
--------70
----------68
------------null
------------null
----------75
------------null
------------null
--90
----null
----100
------null
------101
--------null
--------null

=====二叉树的前序遍历=====
80
50
30
20
25
60
65
70
68
75
90
100
101
=====二叉树的非递归前序遍历=====
80
50
30
20
25
60
65
70
68
75
90
100
101
=====二叉树的中序遍历=====
20
25
30
50
60
65
68
70
75
80
90
100
101
=====二叉树的后序遍历=====
25
20
30
68
75
70
65
60
50
101
100
90
80
二叉树的最小节点值：20
二叉树的最大节点值：101
20是否存在二叉树中：true
200是否存在二叉树中：false
=====删除操作=====
删除最小的值：20
20是否存在二叉树中：false
删除最大的值：101
101是否存在二叉树中：false
100是否存在二叉树中：false