P4095 [HEOI2013]Eden 的新背包问题

P4095 [HEOI2013]Eden 的新背包问题

题解

既然假定第 i 个物品不可以选，那么我们就设置两个数组

dpl[][] 正序选前i个物品，dpr[][] 倒序选前i个物品 ，价格不超过 j 的最大价值

然后正着反着跑 多重背包

最后答案考虑 i 之前的物品的价格和  i 之后的物品的价格，转移如下：

代码

#include<bits/stdc++.h>

using namespace std;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n,q,d,e,ans=;
int dpl[][],dpr[][];
//dpl[][]正序选前i个物品，dpr[][]倒序选前i个物品
struct node{
    int a,b,c;
}thing[];

void pre() //多重背包
{
    for(int i=;i<=n;i++)  //正序背包
    {
        for(int j=;j<=;j++) dpl[i][j]=dpl[i-][j];
        int x=,z=thing[i].c ;
        while(x<=z){
            for(int k=;k>=thing[i].a *x;k--)
               dpl[i][k]=max(dpl[i][k],dpl[i][k-thing[i].a *x]+thing[i].b *x);
            z-=x;
            x<<=;
        }if(z){
            for(int k=;k>=thing[i].a *z;k--)
               dpl[i][k]=max(dpl[i][k],dpl[i][k-thing[i].a *z]+thing[i].b *z);
        }
    }
    for(int i=n;i>=;i--) //倒序背包
    {
        for(int j=;j<=;j++) dpr[i][j]=dpr[i+][j];
        int x=,z=thing[i].c ;
        while(x<=z){
            for(int k=;k>=thing[i].a *x;k--)
               dpr[i][k]=max(dpr[i][k],dpr[i][k-thing[i].a *x]+thing[i].b *x);
            z-=x;
            x<<=;
        }if(z){
            for(int k=;k>=thing[i].a *z;k--)
               dpr[i][k]=max(dpr[i][k],dpr[i][k-thing[i].a *z]+thing[i].b *z);
        }
    }
}

int main()
{
    n=read();
    for(int i=;i<=n;i++)
      thing[i].a =read(),thing[i].b =read(),thing[i].c =read();
    pre();
    q=read();
    for(int i=;i<=q;i++)
    {
        d=read()+; //输入编号是从0开始的
        e=read();ans=;
        for(int j=;j<=e;j++)
          ans=max(ans,dpl[d-][j]+dpr[d+][e-j]);
        printf("%d\n",ans);
    }
    return ;
}

后面附上听课笔记：

◦ N个物品，第i个物品有c[i]个，购买第i个物品需要a[i]元，可获利b[i]的价
值。有m个询问，每次询问：如果第x个物品禁止购买，你有y元的话，能
获得的最大价值是多少？询问之间互相独立。
◦ N<=1000,m<=3*10^5 
>Solution

这是一个经典的问题
◦ 分治+背包
◦ 初始solve(1,n)
◦ 递归的函数到Solve(l,r)，维护的dp数组，记录的是除去[l,r]外的物品的构成的背
包数组。
◦ Solve(l,mid)时，把[mid+1,r]内的物品加入dp数组。
◦ 我们这里定义的加入这个物品u，就是多考虑上这个物品之后构成的dp数组。
若是0/1背包的加入也就是做以下这个操作。
◦ For (int i=n;i>=w[u];i--) dp[i]=max(dp[i],dp[i-w[u]]+v[u]);
◦ 当l=r时，将对应所有的询问在dp数组查询即可。
◦ 单调队列优化的话，复杂度O(n*m*log(n)),每个物品被加进去log次，每次O(m)

代码实现

。由于你要分治求解，所以d表示深度

。

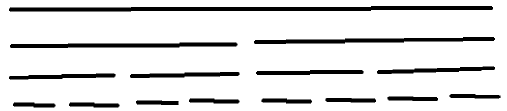
对于每次询问，ans得到答案，id[i]表示询问编号，S[i]表示题目所给出的y

。由于是分治，所以每次都先复制一遍再传递下去

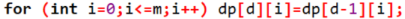
◦ Insert(dp,i)：是在dp数组当中加入i号物品。

全部代码：