RANSAC拟合算法

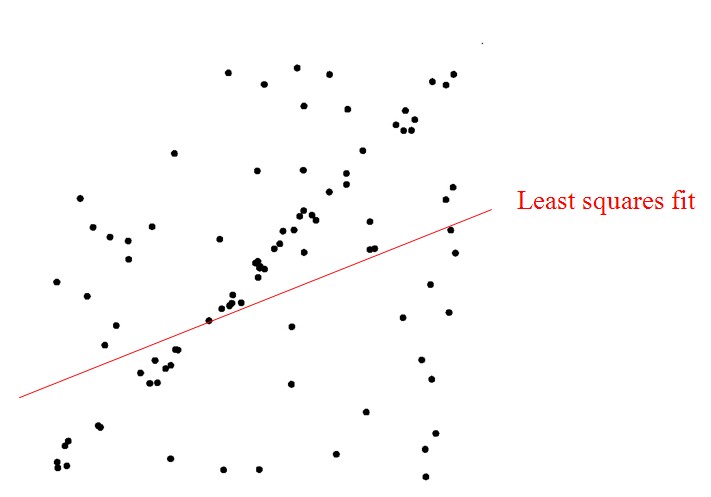
最小二乘法只适合与误差较小的情况。试想一下这种情况，假使需要从一个噪音较大的数据集中提取模型（比方说只有20%的数据时符合模型的）时，最小二乘法就显得力不从心了。

算法简介

随机抽样一致算法(RANdom SAmple Consensus,RANSAC)。它是一种迭代的方法，用来在一组包含离群的被观测数据中估算出数学模型的参数。
RANSAC是一个非确定性算法，在某种意义上说，它会产生一个在一定概率下合理的结果，其允许使用更多次的迭代来使其概率增加。此RANSAC算法在1981年由Fischler和Bolles首次提出。
RANSAC的基本假设是 “内群”数据可以通过几组模型参数来叙述其数据分布，而“离群”数据则是不适合模型化的数据。 数据会受噪声影响,噪声指的是离群，例如从极端的噪声或错误解释有关数据的测量或不正确的假设。
RANSAC假定，给定一组（通常很小）的内群，存在一个程序，这个程序可以估算最佳解释或最适用于这一数据模型的参数。

一、范例

这里用一个简单的例子来说明，在一组数据点中找到一条最适合的线。
假设，此有一组集合包含了内群以及离群，其中内群为可以被拟合到线段上的点，而离群则是无法被拟合的点。
如果我们用简单的最小平方法来找此线，我们将无法得到一条适合于内群的线，因为最小平方法会受离群影响而影响其结果。
而RANSAC，可以只由内群来计算出模型，而且概率还够高。
然而，RANSAC无法保证结果一定最好，所以必须小心选择参数,使其能有足够的概率。

二、算法实现过程

1.在数据中随机选择几个点设定为内群
2.计算适合步骤一中内群的模型
3.把其它刚才没选到的点带入刚才建立的模型中，计算是否为内群
4.记下内群数量，如果有足够多的点被归类为假设的局内点，那么估计的模型就足够合理。
5.重复以上步骤多做几次
6.比较哪次计算中内群数量最多,内群最多的那次所建的模型就是我们所要求的解

这里有几个问题
1.一开始的时候我们要随机选择多少点(n)
2.以及要重复做多少次(k)

三、算法

伪码形式的算法如下所示：
输入：
data —— 一组观测数据
model —— 适应于数据的模型
n —— 适用于模型的最少数据个数
k —— 算法的迭代次数
t —— 用于决定数据是否适应于模型的阀值
d —— 判定模型是否适用于数据集的数据数目
输出：
best_model —— 跟数据最匹配的模型参数（如果没有找到好的模型，返回null）
best_consensus_set —— 估计出模型的数据点
best_error —— 跟数据相关的估计出的模型错误

iterations = 0
best_model = null
best_consensus_set = null
best_error = 无穷大
while ( iterations < k )
maybe_inliers = 从数据集中随机选择n个点
maybe_model = 适合于maybe_inliers的模型参数
consensus_set = maybe_inliers

for ( 每个数据集中不属于maybe_inliers的点 ）
if ( 如果点适合于maybe_model，且错误小于t ）
将点添加到consensus_set
if （ consensus_set中的元素数目大于d ）
已经找到了好的模型，现在测试该模型到底有多好
better_model = 适合于consensus_set中所有点的模型参数
this_error = better_model究竟如何适合这些点的度量
if ( this_error < best_error )
我们发现了比以前好的模型，保存该模型直到更好的模型出现
best_model = better_model
best_consensus_set = consensus_set
best_error = this_error
增加迭代次数
返回 best_model, best_consensus_set, best_error

RANSAC算法的可能变化包括以下几种：
（1）如果发现了一种足够好的模型（该模型有足够小的错误率），则跳出主循环。这样可能会节约计算额外参数的时间。
（2）直接从maybe_model计算this_error，而不从consensus_set重新估计模型。这样可能会节约比较两种模型错误的时间，但可能会对噪声更敏感。

四、参数确定

假设每个点时真正内群的概率为 w

w = 内群的数目/（内群数目+外群数目）
通常我们不知道 w 是多少, w^n是所选择的n个点都是内群的机率, 1-w^n 是所选择的n个点至少有一个不是内群的机率, (1 ? w^n)^k 是表示重复 k 次都没有全部的n个点都是内群的机率, 这边定算法跑 k 次以后成功的机率是p，那么,

1 - p = (1 - w^n)^k
p = 1 - (1 - w^n)^k
所以如果希望成功机率高，p = 0.99, 当n不变时，k越大,p越大, 当w不变时，n越大,所需的k就越大, 通常w未知,所以n 选小一点比较好。

五、优点与缺点

RANSAC的优点是它能鲁棒的估计模型参数。例如，它能从包含大量局外点的数据集中估计出高精度的参数。RANSAC的缺点是它计算参数的迭代次数没有上限；如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果。RANSAC只有一定的概率得到可信的模型，概率与迭代次数成正比。RANSAC的另一个缺点是它要求设置跟问题相关的阀值。
RANSAC只能从特定的数据集中估计出一个模型，如果存在两个（或多个）模型，RANSAC不能找到别的模型。

六、应用

RANSAC算法经常用于计算机视觉，例如同时求解相关问题与估计立体摄像机的基础矩阵。

C语言实现

float Ransac
(
  Point2D32f* points,
  size_t Cnt,
  float *line,
  int numForEstimate,
  float successProbability,
  float maxOutliersPercentage
){

  //float outlierPercentage = maxOutliersPercentage;//估计值
  float numerator = log(1.0f-successProbability);
  float denominator = log(1.0f- pow(1.0-maxOutliersPercentage, numForEstimate));
  //随机抽取一定比例的点
  int ransac_times = (int)(numerator/denominator + 0.5);

  printf("ransac_times： %d\n", ransac_times);
  int numDataObjects = Cnt;
  //int numForEstimate = Cnt*0.1;
  int maxVoteCnt = 0;
  float tempLine[4];
  float inliersPercentage = 0.0;

  int *Chosen = new int[numDataObjects];

  Point2D32f *subPoints = new Point2D32f[numForEstimate];
  int pointCnt = 0;
  int voteCnt = 0;
  for(int i = 0; i < ransac_times; i++)
  {
    //随机抽取
    //randomly select data for exact model fit ('numForEstimate' objects).
        memset(Chosen,0,numDataObjects*sizeof(int));
        int maxIndex = numDataObjects-1;
    for(int j = 0; j < numForEstimate; j++)
    {
      int selectedIndex = rand() % numDataObjects;
      Chosen[selectedIndex] = 1;
    }
    //拟合
    pointCnt = 0;
    for(int k = 0; k < numDataObjects; k++)
    {
      if(Chosen[k])
      {
        subPoints[pointCnt].x = points[k].x;
        subPoints[pointCnt].y = points[k].y;
        pointCnt++;
      }
    }
    FitLine2D(subPoints, pointCnt, tempLine);
    float a = tempLine[1]/tempLine[0];
    float b = tempLine[3] - a*tempLine[2];

    //拟合完整之后要对拟合的结果进行鉴定，选出最优的结果
    voteCnt = 0;
    for(int k = 0; k < Cnt; k++)
    {
      //如果在直线上或者附近
      if(abs(points[k].y - a*points[k].x - b) < 2)
      {
        voteCnt++;
      }
    }

    if(voteCnt > maxVoteCnt)
    {
      maxVoteCnt = voteCnt;
      inliersPercentage = (float)maxVoteCnt/Cnt;
//			printf("a: %f\tb%f\tpercent: %f\n", a, b, inliersPercentage);
      for(int m = 0; m < 4; m++)
      {
        line[m] = tempLine[m];
      }

    }
    //当inliers的比例比较高的时候就可以直接取该值作为最优解
//		if(inliersPercentage > 0.2)
//		{
//			return inliersPercentage;
//		}
  }
  return inliersPercentage;
}