MLN 讨论 —— inference

We consider two types of inference:

1. finding the most likely state of the world consistent with some evidence
2. computing arbitrary conditional probabilities.

We then discuss two approaches to making inference more tractable on large , relational problems:

1. lazy inference , in which only the groundings that deviate from a "default" value need to be instantiated;
2. lifted inference , in which we group indistinguishable atoms together and treat them as a single unit during inference;

3.1 Inference the most probable explanation

A basic inference task is finding the most probable state of the world y given some evidence x, where x is a set of literals;

Formula

For Markov logic , this is formally defined as follows:  $$ \begin{align} arg \; \max_y P(y|x) & = arg \; \max_y \frac{1}{Z_x} exp \left( \sum_i w_in_i(x, \; y) \right) \tag{3.1} \\  & = arg \; \max_y \sum_i w_in_i(x, \; y) \tag{3.1} \end{align}  $$

$n_i(x, y)$: the number of true groundings of clause $i$ ;

The problem reduces to finding the truth assignment that maximizes the sum of weights of satisfied clauses;

Method

MaxWalkSAT:

Repeatedly picking an unsatisfied clause at random and flipping the truth value of one of the atoms in it.

With a certain probability , the atom is chosen randomly;

Otherwise, the atom is chosen to maximize the sum of satisfied clause weights when flipped;

DeltaCost($v$) computes the change in the sum of weights of unsatisfied clauses that results from flipping variable $v$ in the current solution.

Uniform(0,1) returns a uniform deviate from the interval [0,1]

Example

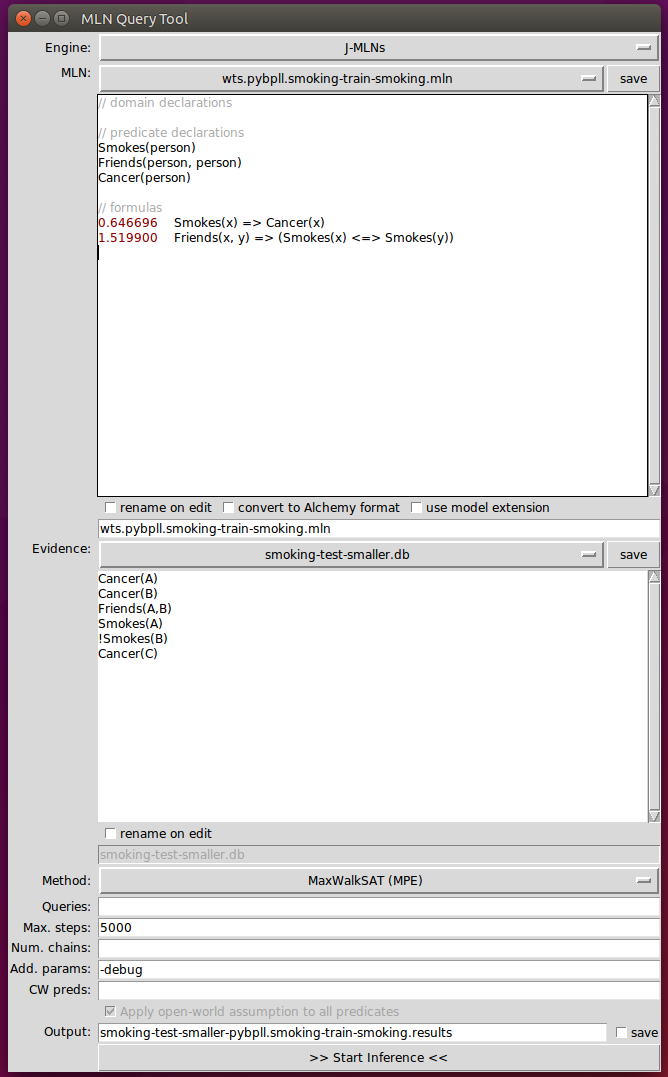
Step1: convert Formula to CNF 

0.646696    $\lnot$Smokes(x) $\lor$ Cancer(x)

1.519900    ( $\lnot$Friends(x,y) $\lor$ $\lnot$Smokes(x) $\lor$ Smokes(y)) $\land$ ( $\lnot$Friends(x,y) $\lor$ $\lnot$Smokes(y) $\lor$ Smokes(x))

Clauses:

1. $\lnot$Smokes(x) $\lor$ Cancer(x)
2. $\lnot$Friends(x,y) $\lor$ $\lnot$Smokes(x) $\lor$ Smokes(y)
3. $\lnot$Friends(x,y) $\lor$ $\lnot$Smokes(y) $\lor$ Smokes(x)

Atoms: Smokes(x) 、Cancer(x) 、Friends(x,y)

Constant: {A, B, C}

Step2: Propositionalizing the domain

The truth value of evidences is depent on themselves;

The truth value of others is assigned randomly;

C:#constant ;          $\alpha(F_i)$: the arity of $F_i$ ;

world size = $\sum_{i}C^{\alpha(F_i)}$     指数级增长！！！

Step3: MaxWalkSAT

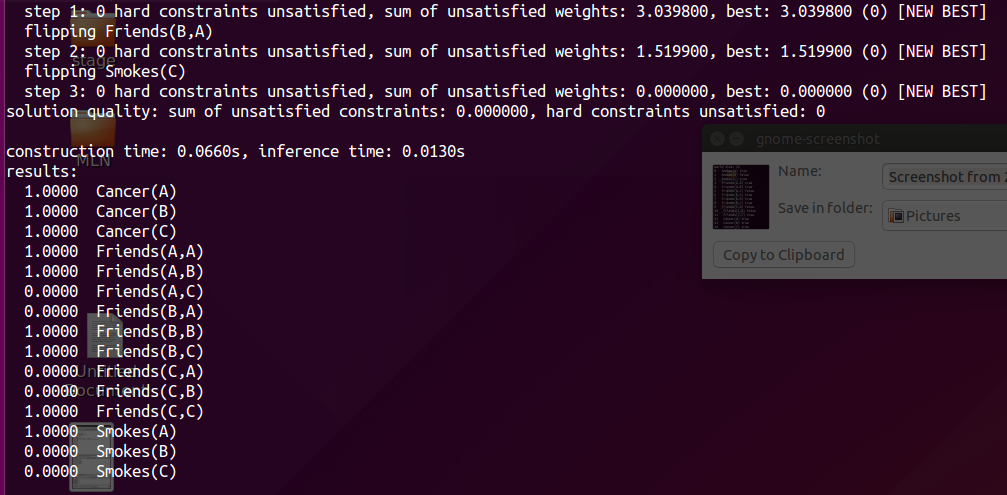
3.2 Computing conditional Probabilities

MLNs can answer arbitraty queries of the form "What is the probability that formula $F_1$ holds given that formula $F_2$ does?". If $F_1$ and $F_2$ are two formulas in first-order logic, C is a finite set of constants including any constants that appear in $F_1$ or $F_2$, and L is an MLN, then $$ \begin{align} P(F_1|F_2, L, C) & = P(F_1|F_2,M_{L,C}) \tag{3.2} \\ & = \frac{P(F_1 \land F_2 | M_{L,C})}{P(F_2|M_{L,C})} \tag{3.2} \\ & = \frac{\sum_{x \in \chi_{F_1} \cap \chi_{F_2} P(X=x|M_{L,C}) }}{\sum_{x \in \chi_{F_2}P(X=x|M_{L, C})}} \tag{3.2} \end{align} $$

where $\chi_{f_i}$ is the set of worlds where $F_i$ holds, $M_{L,C}$ is the Markov network defined by L and C;

Problem

MLN inference subsumes probabilistic inference, which is #P-complete, and logical inference, which is NP-complete;

Method: 数据的预处理

We focus on the case where $F_2$ is a conjunction of ground literals , this is the most frequent type in practice.

In this scenario, further efficiency can be gained by applying a generalization of knowledge-based model construction.

The basic idea is to only construct the minimal subset of the ground network required to answer the query.

This network is construct by checking if the atoms that the query formula directly depends on are in the evidence. If they are, the construction is complete. Those that are not are added to the network, and we in turn check the atoms they depend on. This process is repeated until all relevant atoms have been retrieved;

Markov blanket : parents + children + children's parents  , BFS

example

Once the network has been constructed, we can apply any standard inference technique for Markov networks, such as Gibbs sampling;

Problem

One problem with using Gibbs sampling for inference in MLNs is that it breaks down in the presence of deterministic or near-deterministic dependencies. Deterministc dependencies break up the space of possible worlds into regions that are not reachable from each other, violating a basic requirement of MCMC. Near-deterministic dependencies greatly slow down inference, by creating regions of low probability that are very difficult to traverse.

Method

The MC-SAT is a slice sampling MCMC algorithm which uses a combination of satisfiability testing and simulated annealing to sample from the slice. The advantage of using a satisfiability solver(WalkSAT) is that it efficiently finds isolated modes in the distribution, and as a result the Markov chain mixes very rapidly.

Slice sampling is an instance of a widely used approach in MCMC inference that introduces auxiliary variables, $u$, to capture the dependencies between observed variables, $x$. For example, to sample from P(X=$x$) = (1/Z) $\prod_k \phi_k(x_{\{k\}})$, we can define P(X=$x$, U=$u$)=(1/Z) $\prod_k I_{[0, \; \phi_k(x_{\{k\}})]}(u_k)$