浅谈压缩感知（二十二）：压缩感知重构算法之正则化正交匹配追踪（ROMP）

主要内容：

1. ROMP的算法流程
2. ROMP的MATLAB实现
3. 一维信号的实验与结果
4. 测量数M与重构成功概率关系的实验与结果

一、ROMP的算法流程

正则化正交匹配追踪ROMP算法流程与OMP的最大不同之处就在于从传感矩阵A中选择列向量的标准，OMP每次只选择与残差内积绝对值最大的那一列，而ROMP则是先选出内积绝对值最大的K列（若所有内积中不够K个非零值则将内积值非零的列全部选出），然后再从这K列中按正则化标准再选择一遍，即为本次迭代选出的列向量（一般并非只有一列）。正则化标准意思是选择各列向量与残差内积绝对值的最大值不能比最小值大两倍以上(comparable coordinates)且能量最大的一组(with the maximal energy)，因为满足条件的子集并非只有一组。

二、ROMP的MATLAB实现(CS_ROMP.m)

1、正则化代码Regularize.m

function [val,pos] = Regularize(product,Kin)
%   Regularize
%   Detailed explanation goes here
%   product = A'*r_n;%传感矩阵A各列与残差的内积
%   K为稀疏度
%   pos为选出的各列序号
%   val为选出的各列与残差的内积值
%   Reference:Needell D，Vershynin R. Uniform uncertainty principle and
%   signal recovery via regularized orthogonal matching pursuit.
%   Foundations of Computational Mathematics, ,(): -.
    productabs = abs(product); %取绝对值
    [productdes,indexproductdes] = sort(productabs,'descend'); %降序排列
    for ii = length(productdes):-:
        if productdes(ii)>1e- %判断productdes中非零值个数
            break;
        end
    end
    % Identify:Choose a set J of the K biggest coordinates
    if ii>=Kin
        J = indexproductdes(:Kin); %集合J
        Jval = productdes(:Kin); %集合J对应的序列值
        K = Kin;
    else % or all of its nonzero coordinates,whichever is smaller
        J = indexproductdes(:ii);  %集合J
        Jval = productdes(:ii);  %集合J对应的序列值
        K = ii;
    end
    % Regularize:Among all subsets J0∈J with comparable coordinates
    MaxE = -;  %循环过程中存储最大能量值
    for kk = :K
        J0_tmp = zeros(,K);iJ0 = ;
        J0_tmp(iJ0) = J(kk);  %以J(kk)为本次寻找J0的基准(最大值)
        Energy = Jval(kk)^;  %本次寻找J0的能量
        for mm = kk+:K
            if Jval(kk)<*Jval(mm) %找到符合|u(i)|<=|u(j)|的
                iJ0 = iJ0 + ; %J0自变量增1
                J0_tmp(iJ0) = J(mm); %更新J0
                Energy = Energy + Jval(mm)^; %更新能量
            else %不符合|u(i)|<=|u(j)|的
                break; %跳出本轮寻找，因为后面更小的值也不会符合要求
            end
        end
        if Energy>MaxE %本次所得J0的能量大于前一组
            J0 = J0_tmp(:iJ0); %更新J0
            MaxE = Energy; %更新MaxE，为下次循环做准备
        end
    end
    pos = J0;
    val = productabs(J0);
end

2、ROMP代码CS_ROMP.m

function [ theta ] = CS_ROMP( y,A,K )
%   CS_ROMP
%   Detailed explanation goes here
%   y = Phi * x
%   x = Psi * theta
%    y = Phi*Psi * theta
%   令 A = Phi*Psi, 则y=A*theta
%   现在已知y和A，求theta
%   Reference:Needell D，Vershynin R．Signal recovery from incomplete and
%   inaccurate measurements via regularized orthogonal matching pursuit[J]．
%   IEEE Journal on Selected Topics in Signal Processing，，()：—.
    [m,n] = size(y);
    if m<n
        y = y';%y should be a column vector
    end
    [M,N] = size(A); %传感矩阵A为M*N矩阵
    theta = zeros(N,); %用来存储恢复的theta(列向量)
    At = zeros(M,*K); %用来迭代过程中存储A被选择的列
    pos_num = zeros(,*K); %用来迭代过程中存储A被选择的列序号
    Index = ;
    res = y; %初始化残差(residual)为y
    %Repeat the following steps K times(or until |I|>=2K)
    for ii=:K %迭代K次
        product = A'*res; %传感矩阵A各列与残差的内积
        %[val,pos] = max(abs(product)); %找到最大内积绝对值，即与残差最相关的列
        [val,pos] = Regularize(product,K); %按正则化规则选择原子
        At(:,Index+:Index+length(pos)) = A(:,pos); %存储这几列
        pos_num(Index+:Index+length(pos)) = pos; %存储这几列的序号
        if Index+length(pos)<=M %At的行数大于列数，此为最小二乘的基础(列线性无关)
            Index = Index+length(pos); %更新Index，为下次循环做准备
        else %At的列数大于行数，列必为线性相关的,At(:,:Index)'*At(:,1:Index)将不可逆
            break; %跳出for循环
        end
        A(:,pos) = zeros(M,length(pos)); %清零A的这几列(其实此行可以不要,因为它们与残差正交)
        %y=At(:,:Index)*theta，以下求theta的最小二乘解(Least Square)
        theta_ls = (At(:,:Index)'*At(:,1:Index))^(-1)*At(:,1:Index)'*y; %最小二乘解
        %At(:,:Index)*theta_ls是y在At(:,:Index)列空间上的正交投影
        res = y - At(:,:Index)*theta_ls; %更新残差
        if norm(res)<1e- %Repeat the steps until r=
            break; %跳出for循环
        end
        if Index>=*K %or until |I|>=2K
            break; %跳出for循环
        end
    end
    theta(pos_num(:Index))=theta_ls;%恢复出的theta
end

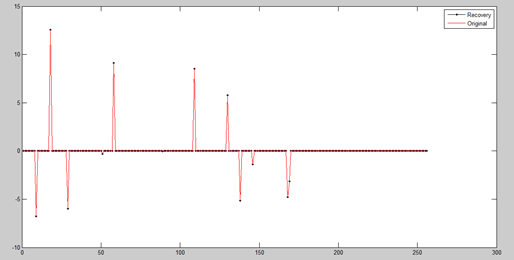
三、一维信号的实验与结果

%压缩感知重构算法测试
clear all;close all;clc;
M = ;%观测值个数
N = ;%信号x的长度
K = ;%信号x的稀疏度
Index_K = randperm(N);
x = zeros(N,);
x(Index_K(:K)) = *randn(K,);%x为K稀疏的，且位置是随机的
Psi = eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
Phi = randn(M,N);%测量矩阵为高斯矩阵
A = Phi * Psi;%传感矩阵
y = Phi * x;%得到观测向量y

%% 恢复重构信号x
tic
theta = CS_ROMP(y,A,K);
x_r = Psi * theta;% x=Psi * theta
toc

%% 绘图
figure;
plot(x_r,'k.-');%绘出x的恢复信号
hold on;
plot(x,'r');%绘出原信号x
hold off;
legend('Recovery','Original')
fprintf('\n恢复残差：');
norm(x_r-x)%恢复残差

四、测量数M与重构成功概率关系的实验与结果

clear all;close all;clc;
%% 参数配置初始化
CNT = ; %对于每组(K,M,N)，重复迭代次数
N = ; %信号x的长度
Psi = eye(N); %x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
K_set = [,,,,]; %信号x的稀疏度集合
Percentage = zeros(length(K_set),N); %存储恢复成功概率

%% 主循环，遍历每组(K,M,N)
tic
for kk = :length(K_set)
    K = K_set(kk);%本次稀疏度
    M_set = K::N;%M没必要全部遍历，每隔5测试一个就可以了
    PercentageK = zeros(,length(M_set));%存储此稀疏度K下不同M的恢复成功概率
    kk
    for mm = :length(M_set)
       M = M_set(mm)%本次观测值个数
       P = ;
       for cnt = :CNT %每个观测值个数均运行CNT次
            Index_K = randperm(N);
            x = zeros(N,);
            x(Index_K(:K)) = *randn(K,);%x为K稀疏的，且位置是随机的
            Phi = randn(M,N);%测量矩阵为高斯矩阵
            A = Phi * Psi;%传感矩阵
            y = Phi * x;%得到观测向量y
            theta = CS_ROMP(y,A,K);%恢复重构信号theta
            x_r = Psi * theta;% x=Psi * theta
            if norm(x_r-x)<1e-%如果残差小于1e-6则认为恢复成功
                P = P + ;
            end
       end
       PercentageK(mm) = P/CNT*;%计算恢复概率
    end
    Percentage(kk,:length(M_set)) = PercentageK;
end
toc
save ROMPMtoPercentage %运行一次不容易，把变量全部存储下来

%% 绘图
S = ['-ks';'-ko';'-kd';'-kv';'-k*'];
figure;
for kk = :length(K_set)
    K = K_set(kk);
    M_set = K::N;
    L_Mset = length(M_set);
    plot(M_set,Percentage(kk,:L_Mset),S(kk,:));%绘出x的恢复信号
    hold on;
end
hold off;
xlim([ ]);
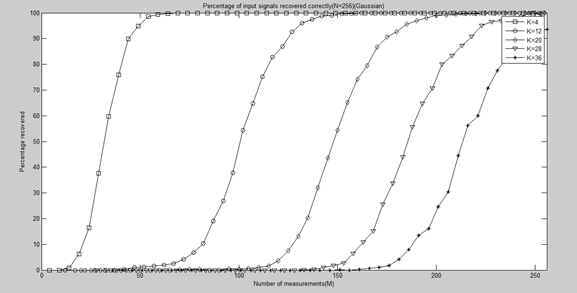
legend('K=4','K=12','K=20','K=28','K=36');
xlabel('Number of measurements(M)');
ylabel('Percentage recovered');
title('Percentage of input signals recovered correctly(N=256)(Gaussian)');

五、参考文章

http://blog.csdn.net/jbb0523/article/details/45268141