POJ 1995 Raising Modulo Numbers (快速幂)

题意：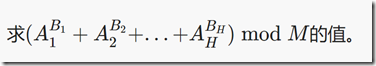

思路：

对于每个幂次方，将幂指数的二进制形式表示，从右到左移位，每次底数自乘，循环内每步取模。

#include <cstdio>

typedef long long LL;

LL Ksm(LL a, LL b, LL p) {
  LL ans = 1;
  while(b) {
    if(b & 1) {
      ans = (ans * a) % p;
    }
    a = (a * a) % p;
    b >>= 1;
  }
  return ans;
}

int main() {
  LL p, a, b;
  int T;
  int n;
  scanf("%d", &T);
  while(T--) {
    scanf("%lld%d", &p, &n);
    LL ans = 0;
    while(n--) {
      scanf("%lld%lld", &a, &b);
      ans = (ans + Ksm(a, b, p)) % p;
    }
    printf("%lld\n", ans);
  }
  return 0;
}